YuQiao0303

[个人笔记]吴恩达深度学习lesson5 week2自然语言处理与词嵌入（Natural Language Processing and Word Embeddings）

这是一篇个人向的笔记。
推荐学习顺序：

（可选）最好掌握线性代数、微积分、概率论的一些基本知识
学习吴恩达机器学习课程
学习吴恩达深度学习的前4课（也可以选择性学习部分内容）即第五课第一周
然后可以学习本课，即吴恩达深度学习第五课的第二周内容
本课程视频
本课程文字版

2.1 词汇表征（Word Representation）
2.2 使用词嵌入（Using Word Embeddings）
2.3 词嵌入的特性（Properties of Word Embeddings）
2.4 嵌入矩阵（Embedding Matrix）
2.5 学习词嵌入（Learning Word Embeddings）
2.6 Word2Vec（Skip-Gram & CBOW）
2.7 负采样（Negative Sampling）
2.8 GloVe 词向量（GloVe Word Vectors）
2.9 情感分类（Sentiment Classification）
2.10 词嵌入除偏（Debiasing Word Embeddings）
课后编程作业一
- notes:
课后编程作业二

2.1 词汇表征（Word Representation）

以前用one-hot 向量表示词，缺点是无法表示词之间的相似性等关系，所有词都是某种意义上等价的。但实际上显然apple、orange、pencil, pen 的相似性不同。
改进的方法：词嵌入 word embeddings。假设一个词有很多特征（属性），比如性别，高贵程度，是否是食物，年龄，size，cost，alive，action，noun，verb之类的。
一种降维可视化的方法：t-SNE算法，来自于Laurens van der Maaten 和 Geoff Hinton的论文。有人说他一般没有PCA常用，但在可视化方面优于PCA。
之所以叫embedding，因为每个词是一个高级向量，所以每个词就向被嵌入在一个高维空间。

2.2 使用词嵌入（Using Word Embeddings）

这章大概讲了三个事：

用word embedding做迁移学习的步骤，如上图所示。（建议补一下第三门课，第二周的2.7迁移学习）
这种弄法适合自己的数据集较小的情况（命名实体识别，用在文本摘要，用在文本解析、指代消解），不太适合自己数据集很大的情况（语言模型、机器翻译）
词嵌入和人脸编码之间有奇妙的关系：词嵌入与人脸编码都是用一个向量（一系列特征值）来表示一个词/一张人脸；但人脸编码可以用于任何一张陌生人脸，词嵌入则有个单词表，只处理这里面的词。

迁移学习课程：
文字版课程
笔记

2.3 词嵌入的特性（Properties of Word Embeddings）

此节用类比推理来直观展现了词嵌入的特性、优势。
例子：求反义词的算法：已知man对woman，求king 对什么？

思路：
反义词的特点是他们的词嵌入的差值为[-2,0,0,0,…,0]. （假设第一个元素是性别），
因此我们问题变成了，求一个词w，其词嵌入是 $e_w$ ，使得 $e_{man} - e_{woman}$ 尽可能接近 $e_{king} - e_{w}$
也就是：让 $Sim (e_{w},e_{king} -e_{man} + e_{woman})$ 尽量小。（Sim是一种相似度评价标准）。

几何角度：
在高维空间中，我们需要找到单词w（正确答案是queen），使这四个点构成平行四边形。
注意如果用t-SNE 来做可视化的话，由于他是非线性的，就不保证还是平行四边形了

下面介绍一种常用的相似度评价标准：余弦相似度。 CosinSimilarity
公式：两个向量的内积除以二者的二范数之积。
得到的结果，就是夹角的余弦值。
夹角越小，余弦值越大，越相似。

2.4 嵌入矩阵（Embedding Matrix）

假设单词表长度为10000，我们特征个数为300 （每一个词嵌入都是300维），则embedding matrix是300行1000列的矩阵，记为 $E$ 。

用embedding matrix 成onehot向量 $O_w$ ，可得到该单词的词嵌入 $e_w$ ,即 $EO_w = e_w$
注意，在表示的时候这样写很方便，在实际应用中这样计算效率很低，建议直接抽取对应的列，而不是用矩阵乘法。

2.5 学习词嵌入（Learning Word Embeddings）

前言:
以前人们用一些方法来学习词嵌入
后来他们发现可以用更简单的方法达到一样好的效果
现在流行的方法都已经十分简单了。但可能直接学就会：啊？为啥这样也行？
因此我们从之前的复杂一点的讲起。

设要学习的词嵌入矩阵为E。

一、one hot * E 输入语言模型的神经网络。其他就是按正常语言模型来。

二、加上时间窗
序列无限长，不可能都输入到神经网络里啊。
所以一般只用到前面固定个数个单词。

三、其他上下文
上面的方法使用目标词之前的k个单词，也可以用他之前的，之后的，相隔了几个的。

一般语言模型用前面几个，但如果是学习词嵌入的话，要求没那么严格。

2.6 Word2Vec（Skip-Gram & CBOW）

思路：
随机选一个词作为上下文c，
在“上下文”一定距离内随机算一个词做目标t。
模型的任务是已知上下文，求目标。（通过求出词典中每个词是目标的概率）
通过这个任务，来学习词嵌入。

大体过程：
要学习的是E和 $\theta_t$
首先用onehot向量成E得到e（词嵌入向量）
然后用要学习的参数 $\theta_t$ 乘 $e_c$ , 放入softmax
softmax已知c，求t的概率就如下表示：

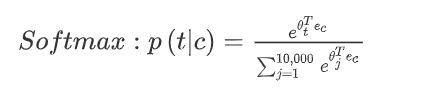
损失函数就是常用的交叉熵：

学完之后就能得到E，叫做Skip-Gram模型。

这套方法的问题：计算太慢。一上来求和就是整个词汇表的长度。
解决方案一：hierarchical softmax：类似二分法。慢慢精确。O(logn)。在实践中不是平衡树，而是把常见的词放在顶部，不常见的放在叶子。
解决方案二：负采样Negative Sampling。详见下一节。

另一个细节：对c的采样不能是均匀的，而应该考虑词的常见和不常见，分层采样。

事实上word2vec有两个，Skip-Gram模型和CBOW，即连续词袋模型（Continuous Bag-Of-Words Model），
CBOW它获得中间词两边的的上下文，然后用周围的词去预测中间的词，这个模型也很有效，也有一些优点和缺点。
总结下：CBOW是从原始语句推测目标字词；而Skip-Gram正好相反，是从目标字词推测出原始语句。CBOW对小型数据库比较合适，而Skip-Gram在大型语料中表现更好。（下图左边为CBOW，右边为Skip-Gram）

2.7 负采样（Negative Sampling）

新的监督学习问题：给定一对单词作为输入x，比如orange和juice，我们要去预测这是否是一对上下文词-目标词（context-target），输出y为0或1。
在这个例子中orange和juice就是个正样本，那么orange和king就是个负样本，我们把它标为0。

先找context词（如orange），找到他们一定距离内的词，称为word（如juice），y为1；
再随机找一个词（如king），生成一组负样本（orange, king,0）. （如果选的词恰好在context的一定距离内也没关系）。重复，一共k次。（一共生成k组负样本）

如何选取k？Mikolov等人推荐小数据集的话，从5到20比较好。如果你的数据集很大，就选的小一点。对于更大的数据集就k等于2到5，数据集越小就越大。

训练方法思路：

把上文中的1000维（1000是例子中的单词表大小）的softmax，改成1000个sigmoid
每次迭代我们只训练采样到的(k+1)个sigmoid

采样技巧：
一种自然的想法一：就用均匀采样，每个词被采样到的概率是1/单词表大小
一种自然的想法二：每个词被采样到的概率是他在这种语言中出现的概率本身
一种经验：不确定该方法是否有理论证明，不过用的人还挺多，效果也不错。 f(wi)是他在语言中出现的概率本身。

2.8 GloVe 词向量（GloVe Word Vectors）

这一节推荐看视频而非纯图文。
GloVe代表用词表示的全局变量（global vectors for word representation）
就是要minimize下面那个式子。
$X_{ij}$ 是单词i和单词j是上下文（相距不超过某规定词数）的次数。
我们希望 $\theta_i^te_j$ 尽可能接近 $logX{ij}$
先对i和j求个和
然后乘一个加权函数f
然后弄b作为偏置（有趣，视频里根本没讲）

加权f的详细介绍：
有的词从来不互为上下文， $X_{ij}$ 为0，log为无穷大，不太好。
于是加权函数f，满足当 $X_{ij}$ 为0时，f为0.
同时，对于this, is ,of, a 这种常见词（称为stop word停止词），给大一点但不过分的权重
不那么常见的词，比如榴莲，给小但不过分小的权重

θ和e对称：
在GloVe方法中，theta和e是对称的。其他方法中则不是。

另一个点：
注意，我们的特征e，他并不是每个轴都像我们最初的例子那样可解释（gender, royal, food, cost…）。他可能是空间中任意的轴，比如不同属性的叠加，分解等：

2.9 情感分类（Sentiment Classification）

情感分类一个最大的挑战就是可能标记的训练集没有那么多，
但是有了词嵌入，即使只有中等大小的标记的训练集，你也能构建一个不错的情感分类器
用词嵌入的好处是能很好的泛化

任务：输入一段话（是一个人对一个餐馆的评价），输出一个星级（这个人相当于给餐馆打了几分）

方法一：平均值运算单元
取输入的这段话的所有词的embedding，求和或求平均，结果喂到softmax分类器（假设是5分类）
这种方法的问题是没考虑词序，一个不字就全完蛋了

方法二：RNN处理词嵌入
词嵌入作为序列，输入RNN，从而解决方法一种的问题。

2.10 词嵌入除偏（Debiasing Word Embeddings）

这一节推荐看视频而非纯图文。

这一节的内容来自以下论文：
[1]Bolukbasi, et al. “Man is to Computer Programmer as Woman is to Homemaker? Debiasing Word Embeddings.”.

一：首先求bias direction：用he,she; male, female 等一对对的词的embedding相减，再求均值。结果就作为gender bias的方向。与它正交的就是与gender毫不相关的方向。

bias direction 和 non-bias direction 分别是全空间的一个子空间（不一定是一维的）。
这里吴老师也简化了原文，原文不是均值，而是SVU（奇异值分解）

二：中和步骤（Neutralize）：
把和性别不相关的中立词（doctor, babisitter, etc.）移动到non-bias direction 上面。
很好移。首先假设求出来的bias direction 为向量g。
实际就是把中立词在bias direction 的分量清除，只保留中立词在non-bias direction上的分量。

修改完的中立词=中立词-中立词在bias direction上的分量
中立词在bias direction上的分量 = d

三：均衡步骤 (Equalize)
把和性别相关，但除了性别不同其他完全一样的词（grandfather, grandmother,）, 弄成沿 non-bias direction 对称。（不然的话，如上图，grandmother和baysitter的距离还是小于grandfather和babysitter，因为grandmother的位置比grandfather更高）。
具体怎么做呢？本节没展开，只说是一些线性代数。（吴老师没展开，但文字版笔记的作者放了一些补充资料，主要是一些公式）
个人感觉一个简单的解法就是到bias direction的距离求平均，然后放上去。

最后一个细节：如何确定哪些词是中立词？
原文作者训练了一个分类器。

完结撒花！

课后编程作业一

词向量的基本操作

主要内容：

计算余弦相似度
单词类比人物
词嵌入纠偏

要写的代码：

def cosine_similarity(u, v):
def complete_analogy(word_a, word_b, word_c, word_to_vec_map):
def neutralize(word, g, word_to_vec_map):
def equalize(pair, bias_axis, word_to_vec_map):

notes:

上文链接有两个问题，如下：
最后的equalize步骤中，公式应如下：
参考本文

最后的equalize结果应如下：
还是参考上面的链接。

cosine similarities before equalizing:
cosine_similarity(word_to_vec_map[“man”], gender) = -0.1171109576533683
cosine_similarity(word_to_vec_map[“woman”], gender) = 0.3566661884627037
cosine similarities after equalizing:
cosine_similarity(e1, gender) = -0.7165727525843935
cosine_similarity(e2, gender) = 0.7396596474928907

课后编程作业二

训练一个模型，输入是一句话，输出是一个emoji表情。

v1：把输入的话的所有单词的embedding求平均，输入如下网络：