李宏毅机器学习笔记p5-p8：误差和梯度下降

---

前言

这篇开始涉及到了我未涉及的领域，也算是机器学习的慢慢深入，虽然知识点是新的，但通过视频和笔记，还是基本可以理解透彻。

---

提示：以下是本篇文章正文内容，下面案例可供参考

误差Error

通过前文的学习，我们了解到当次数越高的时候，模型越复杂的时候，测试效果可能不是很好（出现过拟合现象）
这些误差Error主要来源于bias (偏差) 和 variance(方差)

假设一组数据，期望为$\mu$,方差为${\sigma }^2$

偏差Bias

同一个模型在不同的数据集结果是不一样的。

bias：描述的是根据样本拟合出的模型的输出预测结果的期望与样本真实结果的差距，简单讲，就是在样本上拟合的好不好。

评估x的偏差:
当N样本不够大的时候，平均值m并不等于其期望值
$$m=\frac{1}{N}\sum _n{x}^n\ne \mu$$
但是m的期望是等于$\mu$的
$$\mathrm{E}[\mathrm{m}]=\mathrm{E}[\frac{1}{N}\sum _n{x}^n]=\frac{1}{N}E[\sum _n{x}^n]=\mu$$

varience的值取决于今天取了多少sample
$Var[m]=\frac{{\sigma }^2}{N}$
N比较大，则比较集中，N比较小，则会比较分散

偏差过大

偏差过大导致的结果是欠拟合。
原因：没有很好的训练数据集。
改进方法：重新设计模型。

方差Variance

varience：样本上训练出来的模型在测试集上的表现
$$s^2=\frac{1}{N}\sum _n{(x^n-m)}^2$$
测试$s^2$的期望 ：
$$E[s^2]=\frac{N-1}{N}{\sigma }^2$$
结果：
简单的模型面对多种多样的数据样本方差就会比较小——>训练集影响较小。

方差过大

方差过大的导致的是过拟合。
原因：训练集训练的很好，但在测试集上，方差过大，错误较大。
改进方法：更多的数据。

选择平衡偏差和方差的模型

1.不能因为在你的测试集上误差较小，就认为这个模型好：因为你的测试集只是所有测试数据的一部分。

N-折交叉验证

1.将训练集分成N份。
2.把其中一份作为测试集，把N-1份作为训练集，算出在备选 Model 上 err 的结果。然后选另一份作为测试集，以此类推重复N遍。
3.算出每一种模型的Average error 然后选出Error最小的那一份model。
4.用选出的model训练所有训练集，最后得出结果。

梯度下降

目标：
$${\theta }^{\ast }=\arg \underset{\theta }{\min }L(\theta )$$
L：损失函数，$\theta$:参数(可以是一串列向量)
迭代过程：
$${\theta }^n={\theta }^{n-1}-\eta \nabla L({\theta }^{n-1})$$
$$\nabla L(\theta )=\left[\begin{array}{c}\frac{\partial L({\theta }_1)}{\partial {\theta }_1}\\ \frac{\partial L({\theta }_2)}{\partial {\theta }_2}\\ ⋮\\ \frac{\partial L({\theta }_n)}{\partial {\theta }_n}\end{array}\right]$$
$\eta$：学习率

调整学习率

1.固定学习率

整场learning rate都不改变：
learning rate:太小——>走得很慢（蓝线）；比较大——>走得很快，会导致在谷区振荡（绿线）；超级大——>直接跳跃出谷区，飞出去了。（黄线）

2.自适应学习率——Adagrad

learning rate在改变
调整方法：
刚开始：设置较大的learning rate——>因为离最优点较远
在几次update：慢慢减少自己的learning rate
——————————————————————————————
较好的方法是：每个不同的参数，都给予不同的learning rate——>经典方法：Adagrad

$$\{\begin{array}{c}{w}^{t+1}=w^t-\frac{{\eta }^t}{{\sigma }^t}{g}^t\\ g^t=\frac{\partial L({\theta }^t)}{\partial w}\\ {\sigma }^t=\sqrt{\frac{1}{t+1}\sum _{i=0}^t{(g^i)}^2}\end{array}$$
$${\eta }^t=\frac{n}{\sqrt{t+1}}$$
${\sigma }^t$：是之前参数所有微分的均方根

化简得:
$$w^{t+1}=w^t-\frac{\eta }{\sqrt{\sum _{i=0}^t{(g^i)}^2}}{g}^t$$
改编之后：$\sqrt{\sum _{i=0}^t{(g^i)}^2}$和 $g^t$当t越大的时候，他们造成的影响是反差的
原因是：
最好的步伐：
一个参数：步伐$\propto$一次微分
多个参数：步伐$\propto$一次微分/二次微分
跟adgrad的关系：
$g^t$ ——>一次微分
$\sqrt{\sum _{i=0}^t{(g^i)}^2}$——>反应了二次微分

随机梯度下降

普通的梯度下降：
计算所有的loss，然后再算${\theta }^n$
$${\theta }^n={\theta }^{n-1}-\eta \nabla L({\theta }^{n-1})$$
随机的梯度下降：
只取某一个example算loss function,就可以算${\theta }^n$
优势：在计算相同个数的例子的时候，随机梯度下降法更新的速度更快。

特征缩放

目的：不同的特征所处的范围是类似的

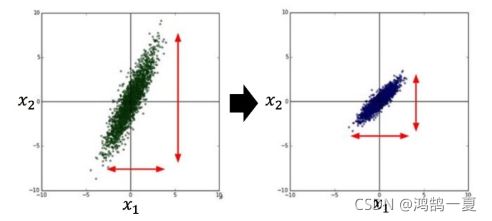
原因：参照上图，当 $x_1$的系数和$x_2$的系数发生一样幅度的变化，明显$x_2$对结果的影响比$x_1$大
转化完之后——>参数更新会比较容易。

方法：
常见方法：
$${x_i}^r=\frac{{x_i}^r-m_i}{{\sigma }_i}$$
$m_i$为同一维度的平均数，${\sigma }_i$为同一维度标准差

梯度下降的理论基础

假设有两个变量${\theta }_1$ ${\theta }_2$
在(a,b)点
利用泰勒展开得
$$L(\theta )\approx L(a,b)+\frac{\partial L(a,b)}{\partial {\theta }_1}({\theta }_1-a)+\frac{\partial L(a,b)}{\partial {\theta }_2}({\theta }_2-b)$$
问题转化为：
$$\begin{array}{cc}\min & L(\theta )\end{array}$$

$$\{\begin{array}{c}{({\theta }_1-a)}^2+{({\theta }_2-b)}^2\le d^2\\ L(\theta )\approx L(a,b)+\frac{\partial L(a,b)}{\partial {\theta }_1}({\theta }_1-a)+\frac{\partial L(a,b)}{\partial {\theta }_2}({\theta }_2-b)\\ \theta =\{{\theta }_1,{\theta }_2\}\end{array}$$
我们可以得出：

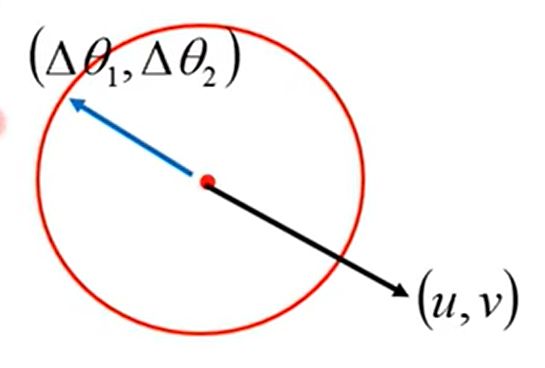
$$\left[\begin{array}{c}{\theta }_1-a\\ {\theta }_2-b\end{array}\right]=-\eta \left[\begin{array}{c}\frac{\partial L(a,b)}{\partial {\theta }_1}\\ \frac{\partial L(a,b)}{\partial {\theta }_2}\end{array}\right]$$
时，$L(\theta )$最小。

变形得
$$\left[\begin{array}{c}{\theta }_1\\ {\theta }_2\end{array}\right]=\left[\begin{array}{c}a\\ b\end{array}\right]-\eta \left[\begin{array}{c}\frac{\partial L(a,b)}{\partial {\theta }_1}\\ \frac{\partial L(a,b)}{\partial {\theta }_2}\end{array}\right]$$
和上文的${\theta }^n={\theta }^{n-1}-\eta \nabla L({\theta }^{n-1})$相同。推导成立。

但前提是：能如此泰勒展开需要学习率足够小才可以。
扩展：上文时泰勒一次展开项，若二次项（牛顿法）则过于繁琐。

总结

提示：这里对文章进行总结：
例如：学习误差包括偏差和方差，里面的那张图真的非常生动形象，比较容易理解。还学习了N-折交叉验证，在我意识里测试集好的话，那模型一定好，看来是我的误解，也算纠正了我错误的地方。然后学习了自适应学习率，在上一章代码有涉及，也提前了解过。通过理论推导梯度下降，是一个看似复杂但可以理解的更加透彻的过程。