西瓜书第四章笔记

4.1 决策树基本概念

顾名思义，决策树是基于树结构来进行决策的。

4.2决策树的构造

图片为转载，侵权则删除

根据上面的伪代码实现的python程序如下：（预测是否贷款，参考了大佬的代码，注释以后补上）

from math import log

"""
函数说明:创建测试数据集
"""
def createdata_set():
    data_set = [[0, 0, 0, 0, 'no'],         #数据集
               [0, 0, 0, 1, 'no'],
               [0, 1, 0, 1, 'yes'],
               [0, 1, 1, 0, 'yes'],
               [0, 0, 0, 0, 'no'],
               [1, 0, 0, 0, 'no'],
               [1, 0, 0, 1, 'no'],
               [1, 1, 1, 1, 'yes'],
               [1, 0, 1, 2, 'yes'],
               [1, 0, 1, 2, 'yes'],
               [2, 0, 1, 2, 'yes'],
               [2, 0, 1, 1, 'yes'],
               [2, 1, 0, 1, 'yes'],
               [2, 1, 0, 2, 'yes'],
               [2, 0, 0, 0, 'no']]
    labels = ['年龄', '有工作', '有自己的房子', '信贷情况']        #分类属性
    return data_set, labels                           #返回数据集和分类属性

def get_max_class(data_set):
    class_dict = {}
    n = len(data_set)
    for i in range(n):
        if data_set[i][-1] in class_dict:
            class_dict[data_set[i][-1]] += 1
        else:
            class_dict[data_set[i][-1]] = 1
    res = 0
    v = 0
    for key in class_dict:
        if res < class_dict[key]:
            res = class_dict[key]
            v = key
    return v

def get_ent(data_set):
    n = len(data_set)
    res = 0.0
    class_dict = {}
    n = len(data_set)
    for i in range(n):
        if data_set[i][-1] in class_dict:
            class_dict[data_set[i][-1]] += 1
        else:
            class_dict[data_set[i][-1]] = 1
    for key in class_dict:
        p = class_dict[key] / n
        res -= p * log(p,2)
    return res

def split_data_set(data_set , attr , attr_val):
    res = []
    for dt in data_set:
        if dt[attr] == attr_val:
            tmp = dt[:attr]
            tmp.extend(dt[attr + 1:])
            res.append(tmp)
    return res


def get_best_label(data_set):
    m = len(data_set[0]) - 1
    ent_d = get_ent(data_set)
    mmax = 0.0
    res = -1
    for i in range(m):
        feature_list = [t[i] for t in data_set]
        feature_set = set(feature_list) #去重
        cnt = ent_d
        for t in feature_set:
            sp_data_set = split_data_set(data_set, i, t)
            ddv = len(sp_data_set) / len(data_set)
            ent_dv = get_ent(sp_data_set)
            cnt -= ddv * ent_dv
        if mmax < cnt:
            mmax = cnt
            res = i
    return res


def create_tree(data_set , labels , feat_labels , feat_num):
    class_list = [t[-1] for t in data_set]
    print('=' * 50)
    if class_list.count(class_list[0]) == len(class_list):
        return class_list[0]
    if len(data_set) == 1:
        return get_max_class(data_set)
    best_feat = get_best_label(data_set)
    best_feat_label = labels[best_feat]
    feat_labels.append(best_feat_label)
    feat_num.append(best_feat)
    # print('bf = {}'.format(best_feat))
    feature_list = [t[best_feat] for t in data_set]
    feature_set = set(feature_list)
    # print(feature_set)
    my_tree = {best_feat_label:{}} #使用字典来表示决策树
    for t in feature_set:
        sp_data_set = split_data_set(data_set , best_feat , t)
        labels_back = []
        print('sp = {}'.format(sp_data_set))
        for k in labels:
            if k != best_feat_label:
                labels_back.append(k)
        my_tree[best_feat_label][t] = create_tree(sp_data_set , labels_back , feat_labels , feat_num)
    my_tree[best_feat_label][-1] = get_max_class(data_set)
    return my_tree

def classify(my_tree , feat_labels , feat_num , test_set):
    for i in range(len(feat_labels)):
        s = feat_labels[i]
        tmp = feat_num[i]
        # print( 's = {}'.format(s) )
        if my_tree[s].get(tmp) != None:
            if my_tree[s].get(tmp).__name__ == 'dict':
                my_tree = my_tree[s].get(tmp)
            else:
                return my_tree[s].get(tmp)
        else: return my_tree[s].get(-1)



if __name__ == '__main__':
    data_set , labels = createdata_set()
    # print(data_set)
    feat_num = []
    feat_labels = []
    my_tree = create_tree(data_set , labels , feat_labels , feat_num)
    print('生成的决策树：{}'.format(my_tree))
    test_set = [0, 1, 0, 1]
    result = classify(my_tree , feat_labels , feat_num , test_set)
    print('是否放贷：{}'.format(result))

运行结果如下：

4.2.1 ID3算法

4.2.2 C4.5算法

ID3算法存在一个问题，就是偏向于取值数目较多的属性，例如：如果存在一个唯一标识，这样样本集D将会被划分为|D|个分支，每个分支只有一个样本，这样划分后的信息熵为零，十分纯净，但是对分类毫无用处。因此C4.5算法使用了“增益率”（gain ratio）来选择划分属性，来避免这个问题带来的困扰。

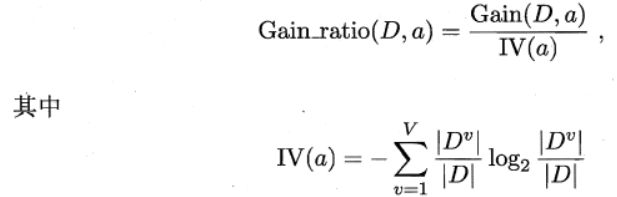
4.2.3 CART算法

CART决策树使用“基尼指数”（Gini index）来选择划分属性，基尼指数反映的是从样本集D中随机抽取两个样本，其类别标记不一致的概率，因此Gini(D)越小越好，基尼指数定义如下：

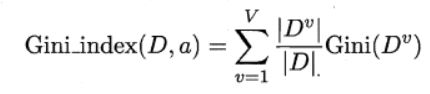
4.3 剪枝处理

处理方法有预剪枝和后剪枝。

4.4 连续值与缺失值处理

连续值处理：
对于连续值的属性，若每个取值作为一个分支则显得不可行，因此需要进行离散化处理，常用的方法为二分法，基本思想为：给定样本集D与连续属性α，二分法试图找到一个划分点t将样本集D在属性α上分为≤t与＞t。
这种情况下的基尼系数的计算公式：

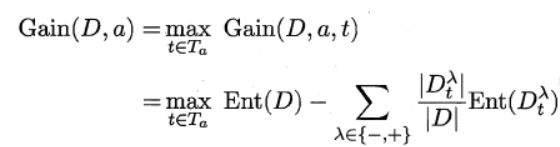
缺失值处理：
对于（1）：通过在样本集D中选取在属性α上没有缺失值的样本子集，计算在该样本子集上的信息增益，最终的信息增益等于该样本子集划分后信息增益乘以样本子集占样本集的比重。即：

对于（2）：若该样本子集在属性α上的值缺失，则将该样本以不同的权重（即每个分支所含样本比例）划入到所有分支节点中。该样本在分支节点中的权重变为：