python冲击二级--初识数据序列类型，斐波那契数列，素数，水仙花数

我们编程会面临处理大量的数据，序列类型的出现，就是为了便于我们处理数据集合。

Python 标准库用 C 实现了丰富的序列类型，列举如下。
容器序列 　　
list、tuple 和 collections.deque 这些序列能存放不同类型的数据。
扁平序列
str、bytes、bytearray、memoryview 和array.array，这类序列只能容纳一种类型。

序列类型还能按照能否被修改来分类。
可变序列 　　
list、bytearray、array.array、collections.deque和 memoryview。
不可变序列 　　
tuple、str 和 bytes。

> 通用序列操作
大多数序列类型，包括可变类型和不可变类型都支持下表中的操作。此表按优先级升序列出了序列操作。在表格中，s 和 t 是具有相同类型的序列，n, i, j 和 k 是整数而 x 是任何满足 s 所规定的类型和值限制的任意对象。in 和 not in 操作具有与比较操作相同的优先级。+ (拼接) 和 * (重复) 操作具有与对应数值运算相同的优先级。

x in s 如果 s 中的某项等于 x 则结果为 True，否则为 False (1) x not in s 如果 s 中的某项等于 x 则结果为 False，否则为 True (1) s + t s 与 t 相拼接
s * n 或 n * s 相当于 s与自身进行 n 次拼接
s[i] s 的第 i 项，起始为 0
s[i:j] s 从 i 到 j 的切片
s[i:j:k] s 从 i 到 j 步长为 k 的切片
len(s) s 的长度
min(s) s 的最小项
max(s)s 的最大项
s.index(x[, i[, j]]) x 在 s 中首次出现项的索引号（索引号在 i 或其后且在 j 之前）
s.count(x) x 在 s 中出现的总次数 相同类型的序列也支持比较。
特别地，tuple 和 list的比较是通过比较对应元素的字典顺序。这意味着想要比较结果相等，则每个元素比较结果都必须相等，并且两个序列长度必须相同。

容器序列，大家想想容器什么样，容器是立体的，这意味着我们不光可以增加他的长度，还可以增高高度，也就是所谓嵌套。类似下面这样：

[
	['a', 'b', 'c', 'd'], 
	['a', 'b', 'c', 'd'],
 	['a', 'b', 'c', 'd'],
 	['a', 'b', 'c', 'd']，
  ]

相对而言扁平序列，就只能像字符串一样，在长度上增加或者减少。

可变类型和不可变类型
我们先来看看示例列表初始化方法：

列表

列表可变，有序，内部对象可重复，非常灵活，存什么都可以，但是这种灵活的代价是性能。

>>> a=[]
>>> a
[]
>>> a=list()
>>> a
[]
>>>

建立一个有0-9数字的列表的几种方法：

>>> list(range(10))#用range初始化，通过调用list函数进行初始化
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

>>> [i for i in range(10)]#列表推导式
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

#下面的语句就是对列表推导式的拆解，可见列表推导易读，简洁，大家都喜欢
>>> a=[]
>>> for i in range(10):
...     a.append(i)
>>> a
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
>>>

学了序列就不得不说切片

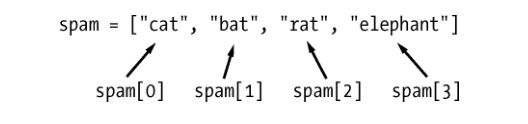
假定列表[‘cat’, ‘bat’, ‘rat’, ‘elephant’]保存在名为 spam 的变量中。Python 代码spam[0]
将求值为’cat’，spam[1]将求值为’bat’，依此类推。列表后面方括号内的整数被称为“下
标”。列表中第一个值的下标是 0，第二个值的下标是 1，第三个值的下标是 2，依此
类推。

>>> li = list("abcdefg")
>>> li#产生一个字母列表
['a', 'b', 'c', 'd', 'e', 'f', 'g']

>>> li[0]
'a'

>>> li[0]+li[-1]
'ag'

>>> li[1:-1]
['b', 'c', 'd', 'e', 'f']

>>> li[0:4]#切片两个数字，包含下标0，但是下标4并不包含，要注意
['a', 'b', 'c', 'd']

>>len(li)
7
>>> li[0::2]
['a', 'c', 'e', 'g']

我们的列表一共有7个元素，下标范围是0-6，切片的语法是start : end : step,第一个start为开始下标，第二个为结束下标，但是产生的数据并不包含最后一个下标数据位置，step是步长，比如li[0::2]所产生的下标就是0,2,4,6，在start的基础上每次增加2.。这带给了我们十分多的灵活性。看到前面的例子有-1，-1就代表最后一个元素，-2代表倒数第二个，以此类推。

下面看几个例子：

>>> li = list(range(10))
>>> li
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

>>> li[::2]
[0, 2, 4, 6, 8]

>>> li[1::2]
[1, 3, 5, 7, 9]

>>> li[::-1]
[9, 8, 7, 6, 5, 4, 3, 2, 1, 0]

>>> li
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

请仔细看好上面的几种操作，最后的结果li并没有变化，可见切片操作会产生一个新的副本，并不会改变原有列表的元素。

s[i] s 的第 i 项，起始为 0
s[i:j] s 从 i 到 j 的切片
如果 i 或 j 为负值，则索引顺序是相对于序列 s 的末尾: 索引号会被替换为 len(s) + i 或 len(s)+ j。但要注意 -0 仍然为 0。

s 从 i 到 j 的切片被定义为所有满足 i <= k < j 的索引号 k 的项组成的序列。如果 i 或 j 大于len(s)，则使用 len(s)。如果 i 被省略或为 None，则使用 0。如果 j 被省略或为 None，则使用len(s)。如果 i 大于等于 j，则切片为空。

s[i:j:k] s 从 i 到 j 步长为 k 的切片
s 从 i 到 j 步长为 k 的切片被定义为所有满足 0 <= n < (j-i)/k 的索引号 x = i + nk 的项组成的序列。换句话说，索引号为 i, i+k, i+2k, i+3*k，以此类推，当达到 j 时停止 (但一定不包括 j)。当 k 为正值时，i 和 j 会被减至不大于 len(s)。当 k 为负值时，i 和 j 会被减至不大于len(s) - 1。如果 i 或 j 被省略或为 None，它们会成为“终止”值 (是哪一端的终止值则取决于k 的符号)。请注意，k 不可为零。如果 k 为 None，则当作 1 处理。

拼接不可变序列总是会生成新的对象。这意味着通过重复拼接来构建序列的运行时开销将会基于序列总长度的乘方。

看看几个经典问题：

斐波那契数列：1，1，2，3，5，8，13，21，34，55，89…
观察特征得知，从第三项开始，每一项都是前两项之和。

我们的问题是计算前20个斐波那契数，并存入列表：

li = [1,1]
#列表内我们提前存入前两项，然后再循环18次
for i in range(18):
    li.append(li[-1]+li[-2])#每次循环让后两项相加得出第三项
    print(li)
                    
=================== RESTART: /home/fujp/Documents/erji.py ===================
[1, 1, 2]
[1, 1, 2, 3]
[1, 1, 2, 3, 5]
[1, 1, 2, 3, 5, 8]
[1, 1, 2, 3, 5, 8, 13]
[1, 1, 2, 3, 5, 8, 13, 21]
[1, 1, 2, 3, 5, 8, 13, 21, 34]
[1, 1, 2, 3, 5, 8, 13, 21, 34, 55]
[1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89]
[1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144]
[1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233]
[1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377]
[1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610]
[1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987]
[1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597]
[1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584]
[1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181]
[1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765]

完成该序列的编程方式还有很多种，以后会遇到的。比如递归，或者用生成器表达式。

质数又称素数。一个大于1的自然数，除了1和它自身外，不能被其他自然数整除的数叫做质数；否则称为合数（规定1既不是质数也不是合数）。

我们现在要计算100以内的素数，并加入列表打印出来。

li = [2,]
#所有的数都可以被1和自身整除，所以我们要用排除法，凡是除了1和它自身，还能别别的数整除那就不是素数。

for i in range(3,100):#循环所有从2到100之间的数
    for k in range(2,i):#从2逐渐递增到这个数本身，
        if i%k == 0:#如果该数能被除了1和自身之外的数整除，则打破循环，测试下一个数
            break
    else:#如果第二个for循环没有被break，则说明这个数是素数，我们添加进列表
        li.append(i)
        

print(li)
=================== RESTART: /home/fujp/Documents/erji.py ===================
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97]
>>> 

这个代码还可以再次优化，是想一个数字，能把它整除的数，会不会超过这个数字的一半，如果不会超过，我们只要在第二个循环里，循环数字数字的一半就好了，这样我们就节省了很多的时间，也算是初级的算法吧。

水仙花数（Narcissistic number）也被称为超完全数字不变（pluperfectdigital invariant, PPDI）、自恋数、自幂数、阿姆斯壮数或阿姆斯特朗数（Armstrong number），水仙花数是指一个 3 位数，它的每个位上的数字的 3次幂之和等于它本身。

li = []
#三位数从100-999循环
for i in range(100,1000):
    g = i%10 #这个数除以10的余数就是该数个位
    s = i//10%10#十位
    b = i//100#百位
    if g**3+s**3+b**3 == i :
        li.append(i)
   
print(li)
=================== RESTART: /home/fujp/Documents/erji.py ===================
[153, 370, 371, 407]
>>> 

下面我们看看列表对象的基本方法：

 ['append', 'clear', 'copy', 'count', 
 'extend', 'index', 'insert', 'pop', 
 'remove', 'reverse', 'sort']

>>> li = [1,3,44,43,2,4,3,0,0,1,1,"abd",]
>>> li.append(1)#接收一个对象，把其添加到列表最后
>>> li
[1, 3, 44, 43, 2, 4, 3, 0, 0, 1, 1, 'abd', 1]
>>> li.append([100,200])#可以是任意对象。
>>> li
[1, 3, 44, 43, 2, 4, 3, 0, 0, 1, 1, 'abd', 1, [100, 200]]


>>> li.pop()#无参数调用默认抛出列表最后一项，并把该项从列表删除
[100, 200]
>>> li.pop(1)#带参数，就抛出该下标表示的对象，并在列表中删除
3
>>> li
[1, 44, 43, 2, 4, 3, 0, 0, 1, 1, 'abd', 1]

>>> li.index(44)#在列表中查询44的下标
1
>>> li.index(1,2)#从下标2开始向后寻找值为1的下标
8
>>> li.index(1,2,7)#在下标2到7的范围内寻找值为1的下标，没找到引发错误
Traceback (most recent call last):
  File "", line 1, in <module>
    li.index(1,2,7)
ValueError: 1 is not in list


>>> li.insert(0,"aabb")#把参数2，插入到列表下标0位置
>>> li
['aabb', 1, 44, 43, 2, 4, 3, 0, 0, 1, 1, 'abd', 1]


>>> li.remove(1)#移除列表中值为1的项，从前到后第一个找到的。
>>> li
['aabb', 44, 43, 2, 4, 3, 0, 0, 1, 1, 'abd', 1]
>>> li.remove(43)
>>> li
['aabb', 44, 2, 4, 3, 0, 0, 1, 1, 'abd', 1]


>>> li.count(0)#计算参数在里表中的数量
2
>>> li.count(1)
3
>>> 

>>> li
['aabb', 44, 2, 4, 3, 0, 0, 1, 1, 'abd', 1]
>>> li.extend("abcd")#接收一个可迭代对象，把元素一个一个加入到列表后面
>>> li
['aabb', 44, 2, 4, 3, 0, 0, 1, 1, 'abd', 1, 'a', 'b', 'c', 'd']
>>> li.extend([44,55,66,77])#注意和append的区分
>>> li
['aabb', 44, 2, 4, 3, 0, 0, 1, 1, 'abd', 1, 'a', 'b', 'c', 'd', 44, 55, 66, 77]


>>> li
['aabb', 44, 2, 4, 3, 0, 0, 1, 1, 'abd', 1, 'a', 'b', 'c', 'd', 44, 55, 66, 77]
>>> li.reverse()#列表反向
>>> li
[77, 66, 55, 44, 'd', 'c', 'b', 'a', 1, 'abd', 1, 1, 0, 0, 3, 4, 2, 44, 'aabb']

>>> li
[77, 66, 55, 44, 'd', 'c', 'b', 'a', 1, 'abd', 1, 1, 0, 0, 3, 4, 2, 44, 'aabb']
>>> li.clear()#清除列表内容
>>> li
[]


>>> a = [22,11,55,77,3,2,16,7]
>>> a.sort()#排序默认升序排列
>>> a
[2, 3, 7, 11, 16, 22, 55, 77]
>>> a.sort(reverse=True)#设置reverse为True,则降序排列
>>> a
[77, 55, 22, 16, 11, 7, 3, 2]
>>> 
>>> help(a.sort)
Help on built-in function sort:

sort(*, key=None, reverse=False) method of builtins.list instance
    Stable sort *IN PLACE*.

我们看到sort方法接收两个关键字参数，key可以接收一个函数对象，返回用于排序的值。

列表是所有序列中最灵活的，我们编程中会经常用到，大家一定要把列表的基本方法，参数，烂熟于胸。

虽然列表的灵活性给了我们很大的便利，但是同时也会带来一些困扰

[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
>>> for  i in li:
	li.remove(i)

我们本来是想删除列表的所有数据，大家可以打印一下看看结果。
所以我们循环列表的时候最好用下标，或者用列表的副本：
for i in range(len(li)) 或者 for i in li[:]

我们有一组有坐标组成的二维列表：

>>> li = [
    [1,10],
    [-5,-20],
    [3,6],
    [18,20]
    ]
>>> li[0]
[1, 10]
>>> li[0][0]
1
>>> li[0][1]
10
>>> 

>>> for i in li:
	print(i)

	
[1, 10]
[-5, -20]
[3, 6]
[18, 20]
>>> for  i in li:
	print(i[0],i[1])

	
1 10
-5 -20
3 6
18 20
>>> 

理解一下上面的代码，你就会知道对于二维列表如何操作。

元组

元组是不可变序列，通常用于储存异构数据的多项集。

初始化方法

>>> a=()
>>> type(a)
<class 'tuple'>

>>> a=tuple(range(10))
>>> a
(0, 1, 2, 3, 4, 5, 6, 7, 8, 9)
>>> 

元组的方法只有两个’count’, ‘index’，使用方法与列表一样，基于元组的不可变特性，所以元组没有列表的增加，删除，插入，修改等方法，那如果要修改元组怎么办呢。

>>> t
(0, 1, 2, 3, 4, 5, 6, 7, 8, 9)
>>> t[0]=100
Traceback (most recent call last):
  File "", line 1, in <module>
    t[0]=100
TypeError: 'tuple' object does not support item assignment
>>> t1 = list(t)
>>> t1
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
>>> t1[0] = 100
>>> t = tuple(t1)
>>> t
(100, 1, 2, 3, 4, 5, 6, 7, 8, 9)
>>> 

通过列表和元组的相互转换，来修改元组中的值。

下面再看一个例子：

>>> li = [[1,2,3]]*3
>>> li
[[1, 2, 3], [1, 2, 3], [1, 2, 3]]
>>> li[0][0] = 1000
>>> li
[[1000, 2, 3], [1000, 2, 3], [1000, 2, 3]]
>>> 

我知更改了第一项第一个的值，为什么三项的值都变了，基于列表的可变特性，用乘法增加列表的时候，其实每一个都是第一个的引用，其实这三项是同一个列表。

>>> a, b, c = li
>>> a
[1000, 2, 3]
>>> b
[1000, 2, 3]
>>> c
[1000, 2, 3]
>>> id(a)
140618514605000
>>> id(b)
140618514605000
>>> id(c)
140618514605000

id(object)
返回对象的“标识值”。该值是一个整数，在此对象的生命周期中保证是唯一且恒定的

通过查看id，我们发现这三个列表完全是一个。所以大家在操作列表的时候，一定要注意检查，避免程序出错。