二叉树的遍历 中序线索二叉树

---

前言

在N个节点的二叉树中，每个节点有2个指针，所以一共有2N个指针，除了根节点以外，每一个节点都有一个指针从它的父节点指向它，所以一共使用了N-1个指针，所以剩下2N-(N-1)也就是N+1个空指
针；

如果能利用这些空指针域来存放指向该节点的直接前驱或是直接后继的指针，则可由此信息直接找到在该遍历次序下的前驱节点或后继节点，从而比递归遍历提高了遍历速度，节省了建立系统递归栈所使用的存储空间；

这些被重新利用起来的空指针就被称为线索（Thread），加上了线索的二叉树就是线索二叉树。

实现思路：按某种次序遍历二叉树，在遍历过程中用线索取代空指针即可。以中序遍历为例，首先找到中序遍历的开始节点，然后利用线索依次查找后继节点即可。

由于它充分利用了空指针域的空间（等于节省了空间），又保证了创建时的一次遍历就可以终生受用前驱、后继的信息（这意味着节省了时间），所以在实际问题中，如果所使用的二叉树需要经常遍历或查找节点时需要某种遍历中的前驱和后继，那么采用线索二叉链表的存储结构就是不错的选择。

---

一、中序遍历的特点：投影

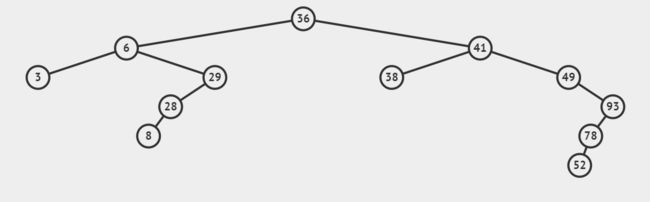
对于上面的一棵二叉树，我们进行中序遍历，即先左节点，根节点，再右节点。

可以得到中序遍历的次序为：3,6,8,28,29,36,38,41,49,52,78,93.

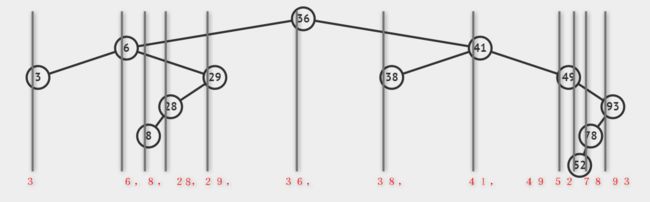
可以看到，二叉树的投影序列，就是中序遍历的序列。

---

同时我们还看到一个现象，如下图。

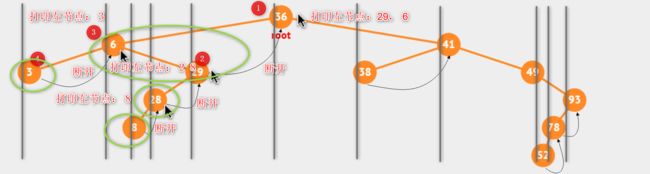
根据投影的定义，根节点（73）的前驱节点，应该是根节点左边最靠近它的节点。

可以看到，垂线2相比垂线3，垂线2肯定比垂线3更靠近根节点（73），因为垂线2的节点（70）是垂线3的节点（62）的右节点；并且，节点（54）永远只能无线逼近节点（62）。因此，节点（70）的投影永远是最靠近根节点（73），节点（70）就是根节点（73）的前驱节点。

---

二、中序线索二叉树

根据中序遍历的定义，中序线索二叉树应该是这样的：

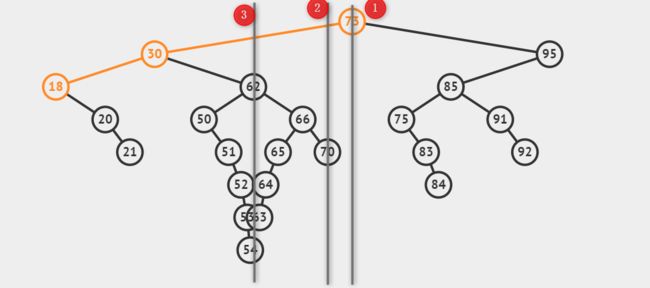
中序遍历下，找某个节点的前驱节点，就是某个节点的左子节点不断向右查找。当前节点的左节点的最右节点，就是当前节点的前驱节点，示意图如下。

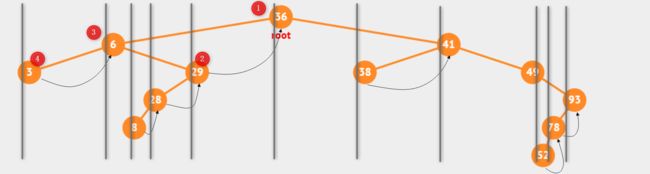
看标记①，它的前驱节点是，从它的左节点不断向右查找，一直找到标记②，此时②就是①的前驱节点。

其他的类似标记③，它的前驱节点从它的左节点向右查找，由于标记④右节点为空，因此④就是③的前驱节点。

---

三、代码思路

主要思路其实就是两个：建立线索，拆掉线索。

因为建立线索的过程中，改变了原有二叉树的结构，叶子节点的空指针指向了其他节点。所以要记得，建立线索后，还要拆掉建立的线索。

怎么记住建立的线索，并且把建立的线索拆掉？

方法就是，每次拿到当前节点（curr_node），就去寻找当前节点（curr_node）的前驱节点（即当前节点的左节点，不断向右查找）。如果在找前驱节点的过程中，一直找到NULL空节点，说明当前节点（curr_node）还没有建立线索，因此就找到了当前节点（curr_node）的前驱节点；如果查找前驱节点的过程中，发现前驱节点指向了当前节点（curr_node），此时就应该断开指向当前节点（curr_node）的线索。于是当前节点（curr_node）的右节点就成为新的当前节点（curr_node）。

---

举例，如下图。

因为我们是中序线索二叉树，当前节点（curr_node）为root，我们先找当前节点（curr_node）的前驱节点，找到了前驱节点（29），此时前驱节点（29）指向当前节点（curr_node）。于是当前节点（curr_node）的左节点（6）成为新的当前节点（curr_node）。

当前节点（curr_node）（6）继续找前驱节点，找到了前驱节点（3）。于是节点（3）成为新的当前节点（curr_node）。

当前节点（curr_node）（3）找前驱节点，它的左节点为空，因此没有前驱节点。于是当前节点（curr_node）（3）的右节点成为新的当前节点（curr_node）（6）。

当前节点（curr_node）（6）找前驱节点，发现节点（3）的右节点与当前节点（curr_node）相同，因此此时应该拆掉这个“线索”，节点（3）的右节点变为空，然后当前节点（curr_node）（6）的右节点（29）成为新的当前节点（curr_node）。

以此类推。

---

三、代码

本质上，因为对二叉树的遍历都是采用中序线索二叉树，所以建立线索二叉树的代码都是一样，只是不同的打印处理才有了不同的前序/中序/后序遍历顺序。

前序遍历（根节点，左节点，右节点）的时机发生在：
1）当前节点找到它的前驱节点时，当前节点就打印；
2）当前节点的左节点为空，当前节点就打印；

中序遍历（左节点，根节点，右节点）的时机发生在：
1）当前节点的左节点为空，当前节点就打印；
2）当前节点断开线索时，当前节点就打印；

---

前序遍历：

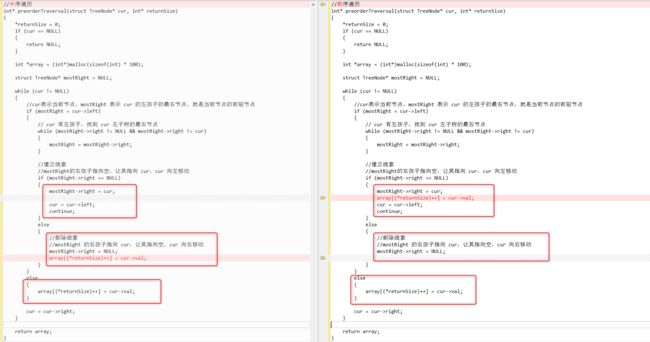
//前序遍历
int* preorderTraversal(struct TreeNode* cur, int* returnSize)
{
    *returnSize = 0;
    if (cur == NULL)
    {
        return NULL;
    }

    int *array = (int*)malloc(sizeof(int) * 100);

    struct TreeNode* mostRight = NULL;

    while (cur != NULL)
    {
        //cur表示当前节点，mostRight 表示 cur 的左孩子的最右节点，就是当前节点的前驱节点
        mostRight = cur->left;
        if (mostRight != NULL)
        {
            // cur 有左孩子，找到 cur 左子树的最右节点
            while (mostRight->right != NULL && mostRight->right != cur)
            {
                mostRight = mostRight->right;
            }

            //建立线索
            //mostRight的右孩子指向空，让其指向 cur，cur 向左移动
            if (mostRight->right == NULL)
            {
                mostRight->right = cur;
                array[(*returnSize)++] = cur->val;
                cur = cur->left;
                continue;
            }
            else
            {  
                //删除线索
                //mostRight 的右孩子指向 cur，让其指向空，cur 向右移动
                mostRight->right = NULL;
            }
        }
        else
        {
            array[(*returnSize)++] = cur->val;
        }

        cur = cur->right;
    }

    return array;
}

---

中序遍历：

//中序遍历
int* inorderTraversal(struct TreeNode* cur, int* returnSize)
{
    *returnSize = 0;
    if (cur == NULL)
    {
        return NULL;
    }

    int *array = (int*)malloc(sizeof(int) * 100);

    struct TreeNode* mostRight = NULL;

    while(cur != NULL)
    {

        if (mostRight = cur->left)
        {
            while (mostRight->right != NULL && mostRight->right != cur)
            {
                mostRight = mostRight->right;
            }

            // 建立线索
            if (mostRight->right == NULL)
            {
                mostRight->right = cur;
                cur = cur->left;
                continue;
            }
            else
            {
                //删除线索
                mostRight->right = NULL;
                array[(*returnSize)++] = cur->val;
            }
        }
        else
        {
            array[(*returnSize)++] = cur->val;
        }

        cur = cur->right;
    }

    return array;
}

---

后序遍历：

//翻转链表
struct TreeNode* reverseNode(struct TreeNode* cur)
{
    struct TreeNode* head = NULL;
    struct TreeNode* new_head = NULL;

    while (cur)
    {
        head = cur->right;
        cur->right = new_head;

        new_head = cur;
        cur = head;
    }

    return new_head;
}

//打印
void printNode(struct TreeNode* head, int* returnSize, int *array)
{
    struct TreeNode* tail = reverseNode(head);
    struct TreeNode* cur = tail;

    while (cur)
    {
        array[(*returnSize)++] = cur->val;
        cur = cur->right;
    }

    reverseNode(tail);
}

int* postorderTraversal(struct TreeNode* cur, int* returnSize)
{
    *returnSize = 0;
    if (cur == NULL)
    {
        return NULL;
    }

    int *array = (int*)malloc(sizeof(int) * 100);

    struct TreeNode* head = cur;
    struct TreeNode* mostRight = NULL;

    while(cur != NULL)
    {

        if (mostRight = cur->left)
        {
            while (mostRight->right != NULL && mostRight->right != cur)
            {
                mostRight = mostRight->right;
            }

            // 建立线索
            if (mostRight->right == NULL)
            {
                mostRight->right = cur;
                cur = cur->left;
                continue;
            }
            else
            {
                //删除线索
                mostRight->right = NULL;
                printNode(cur->left, returnSize, array);
            }
        }

        cur = cur->right;
    }

    printNode(head, returnSize, array);
    return array;
}