1.图形学-矩形中的线段的裁剪Cohen-Sutherland算法(附带源码)
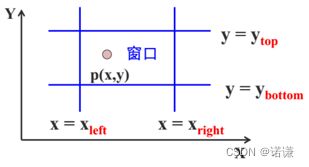
1.矩形中点的裁剪
判断一个点是否在一个矩形中,必须满足:
- 矩形左边的X <= 点的X <= 矩形右边的X
- 矩形顶部的Y <= 点的Y <= 矩形底部的Y
2.矩形窗口直线的裁剪
分为4种,本章只学习直接求交算法、Cohen-Sutherland算法(编码裁剪算法)
3.直接求交算法(复杂图形裁剪的基础)
对于每条线段(P1,P2)分为三种情况处理:
(1) 若P1,P2完全在窗口内,则显示该线段
线段的p1和p2都要满足以下要求
- Xleft <= 点的X <= Xright
- Y bottom<= 点的Y <= Ytop
(2)若P1,P2在窗口外且无交点,则丢弃该线段。 线段的p1(x1,y1)和p2(x2,y2)满足以下要求之一
(x1 < Xleft && x2< Xleft) ||
(x1 > Xright && x2> Xright) ||
(y1 < Ybottom && y2< Ybottom) ||
(y1 > Ytop && y2 > Ytop)(3)若线段不满足(1)或(2)的条件,则在交点处把线段分为两段。其中一段完全在窗口外,可弃之。然后对另一段重复上述处理
如下图GH为例:
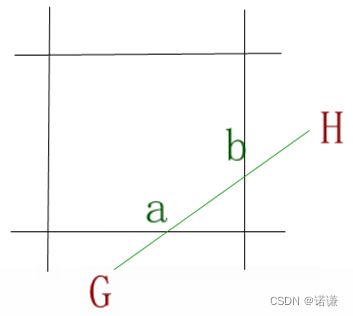
由于G和H在窗口外且与窗口有相交,所以不满足(1)或(2)的条件,然后将交点a处把线段分为两段: Ga、aH、由于Ga在窗口外,则重复执行aH线段处理、直到得出最后为ab线段
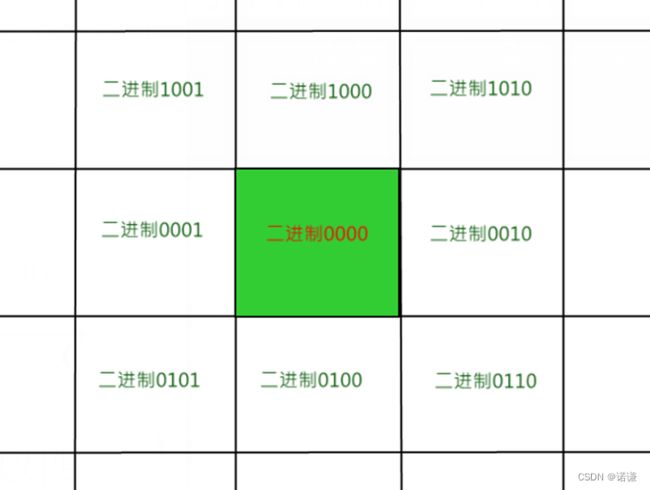
4.Cohen-Sutherland算法(编码裁剪算法)
在直接求交算法的基础上,对窗口进行延伸得到九个区域,对每个区域进行编码(上下右左).如下图所示:
裁剪线段规律如下所示(code1为线段端点1, code2为线段端点2):
- (1) code1 | code2 = 0 则表示在窗口内,则显示该线段
- (2) code1 & code2 != 0 则表示完全在窗口外且不相交, 则丢弃该线段
- (3) 若线段不满足(1)或(2)的条件,则在交点处把线段分为两段。其中一段完全在窗口外,可弃之。然后对另一段重复上述处理
比如有一条线段与界面相交如下所示:
P1(code1) = 0001
P2(code2) = 1000由于code1| code2 != 0 且 code1 & cpde2 = 0,得出线段与界面相交, 则在交点处把线段分为两段。其中一段完全在窗口外,可弃之。然后对另一段重复上述处理
如何计算线段p1(x1,y1)和p2(x2,y2)在窗口边界的交点?
很简单,根据斜率比乘上窗口边界的值在加上偏移值即可得出.对于x和y的公式如下所示:
y = y1 + 斜率 * (x - x1)
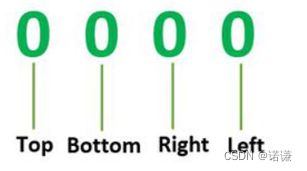
x = x1 + (1 / 斜率) * (y - y1) 窗口的上下左右编码为(1000)、(0100)、(0010)、(0001),如下所示:
if(0001 & code !=0) {
x = Xleft; y = y1+((y2-y1)/(x2-x1))*(Xleft-x1);
} else if(0010 & code != 0) {
x = Xright; y = y1+((y2-y1)/(x2-x1))*(Xright-x1);
} else if(0100 & code != 0) {
y = Ybottom; x = x1+((x2-x1)/(y2-y1))*(Ybootom-y1);
} else if(0010 & code != 0) {
y = Ytop; x = x1+((x2-x1)/(y2-y1))*(Ytop-y1);
}具体代码如下所示:
#include
using namespace std;
// 定义9个区域代码
const int INSIDE = 0; // 0000
const int LEFT = 1; // 0001
const int RIGHT = 2; // 0010
const int BOTTOM = 4; // 0100
const int TOP = 8; // 1000
// 定义一个裁剪矩形
const int x_max = 10;
const int y_max = 8;
const int x_min = 4;
const int y_min = 4;
// 对线段端点进行区域编码
int computeCode(double x, double y)
{
// initialized as being inside
int code = INSIDE;
if (x < x_min) // to the left of rectangle
code |= LEFT;
else if (x > x_max) // to the right of rectangle
code |= RIGHT;
if (y < y_min) // below the rectangle
code |= BOTTOM;
else if (y > y_max) // above the rectangle
code |= TOP;
return code;
}
// Cohen-Sutherland算法
// 剪切一条线段 P1 = (x2, y2) to P2 = (x2, y2)
void cohenSutherlandClip(double x1, double y1,
double x2, double y2)
{
// 解析编码
int code1 = computeCode(x1, y1);
int code2 = computeCode(x2, y2);
bool accept = false; // accept为true表示可以显示
while (true) {
if ((code1 == 0) && (code2 == 0)) { // 如果两个端点都在矩形内
accept = true;
break;
}
else if (code1 & code2) { // 完全在窗口外且不相交, 则丢弃该线段
break;
}
else { // 部分线段位于矩形
int code_out;
double x, y;
// 判断哪个端点在矩形外部
if (code1 != 0)
code_out = code1;
else
code_out = code2;
// 公式 y = y1 + 斜率 * (x - x1),
// x = x1 + (1 / 斜率) * (y - y1)
// 对矩形外部的端点进行裁剪
if (code_out & TOP) {
x = x1 + (x2 - x1) * (y_max - y1) / (y2 - y1);
y = y_max;
}
else if (code_out & BOTTOM) {
x = x1 + (x2 - x1) * (y_min - y1) / (y2 - y1);
y = y_min;
}
else if (code_out & RIGHT) {
y = y1 + (y2 - y1) * (x_max - x1) / (x2 - x1);
x = x_max;
}
else if (code_out & LEFT) {
y = y1 + (y2 - y1) * (x_min - x1) / (x2 - x1);
x = x_min;
}
//找到交点x, y, 进行替换,弃掉外部的线段
if (code_out == code1) {
x1 = x;
y1 = y;
code1 = computeCode(x1, y1);
}
else {
x2 = x;
y2 = y;
code2 = computeCode(x2, y2);
}
}
}
if (accept) {
cout << "Line accepted from " << x1 << ", "
<< y1 << " to " << x2 << ", " << y2 << endl;
// 用户可以在这里添加代码来显示矩形
}
else
cout << "Line rejected" << endl;
}
int main()
{
// 添加第一条线段 (5, 5),(7, 7)
cohenSutherlandClip(5, 5, 7, 7);
// 添加第一条线段 (7, 9), (11, 4)
// P21 = (7, 9), P22 = (11, 4)
cohenSutherlandClip(7, 9, 11, 4);
// 添加第三条线段 (1, 5), (4, 1)
cohenSutherlandClip(1, 5, 4, 1);
return 0;
}
小结:
本算法只支持矩形窗口、如果是其它形状的窗口则不行、
并且只适合零散的线条裁剪,如果是连续的一条多折线,那么会进行很多重复计算
下章学习:
2.qt-Cyrus-Beck算法(凸多边形的线裁剪算法-C++实现)_诺谦的博客-CSDN博客