GIN:图同构网络
论文标题:How Powerful are Graph Neural Networks?
论文链接:https://arxiv.org/abs/1810.00826
论文来源:ICLR 2019
一、概述
目前的GNN框架大多遵循递归邻域聚合(或者消息传递)框架,并且已经出现各种GNN变种。然而,新的GNN设计大多基于经验直觉、启发式和实验试错。目前,对神经网络的性质和局限性的理论认识较少,对神经网络表征能力的形式化分析也比较有限。
本文提出一种理论框架,用于分析GNN的表征能力。本文受到Weisfeiler-Lehman (WL)图同构测试的启发,WL测试类似于GNN,也通过聚合邻域节点特征来递归更新节点特征向量,以此来区分不同的图。WL测试是一种性能优越的算法,这主要得益于其单射的(injective)聚合更新过程,能够将不同的节点邻域映射到不同的特征向量。本文的一个核心观点是如果GNN的聚合模式具备充分的表达能力且能够建模单射函数,那么其就能够拥有像WL测试一样的鉴别能力。
形式化地来说,一个节点的邻域可以被看做是一个multiset,也就是一个可以包含重复元素的set,因此GNN中的聚合可以看做是multiset上的聚合函数。为了能够具备充分的表达能力,一个GNN就必须能够聚合不同的multiset到不同的表示。
本文的主要结果如下:
①本文显示GNN在识别图结构方面,WL测试是能达到的性能的上限;
②阐述了GNN达到WL测试的性能时在邻域聚合和readout函数方面应该满足的条件;
③识别出一些GNN变种(比如GCN、GraphSAGE等)不能识别的图结构;
④开发了一种全新的GNN变种,即图同构网络(Graph Isomorphism Network, GIN),其鉴别能力与WL测试相当。
二、预备知识
图神经网络
使用表示一个图,中节点的特征向量为。本文主要关注图分类任务。
GNN利用图的结构与节点特征来学习图中节点的特征向量或者整个图的表示。GNN通常遵循邻域聚合策略来更新其节点表示,GNN的第层可以表示为:
❝ ❞
是节点在第层的特征向量。我们使用来初始化,是节点的邻域节点。与的选择对于GNN来说是重要的。在GraphSAGE的pooling变种中,函数被设置为:
❝ ❞
是一个可学习的矩阵,代表max-pooling,另外阶段可以是拼接加上一个线性映射。
而在GCN中,和的设置如下:
❝ ❞
对于图级别的任务,另外需要一个函数来聚合节点特征以获得图级别的特征:
❝ ❞
具体的可以采用相加等图池化函数。
Weisfeiler-Lehman测试
图同构问题讨论的是两个图在拓扑上是否相同。这个问题具备相当的挑战性,目前尚无多项式复杂度的算法。除了一些极端情况之外,WL图同构测试是一种有效的、计算效率高的算法,用于区分广泛的图。WL测试的一维形式“naïve vertex refinement”算法类似于GNN中的聚合,具体做法是迭代地进行:
①聚合节点的标签和其邻域;
②利用哈希函数来将聚合的标签映射成新的标签。
这里的标签可以理解为一维条件下的节点特征。当在某一次迭代过程后如果两个图的节点标签有所不同,则认为这两个图是非同构的。
WL子树核(subtree kernel)是一种基于WL测试的方法,该算法衡量图之间的相似性。算法使用WL测试中不同迭代过程中的节点标签数量来作为图的特征向量。直观上来看,一个节点在WL测试第次迭代后的标签表示的是一个高为且以该节点为根节点的子树结构,如下图所示:
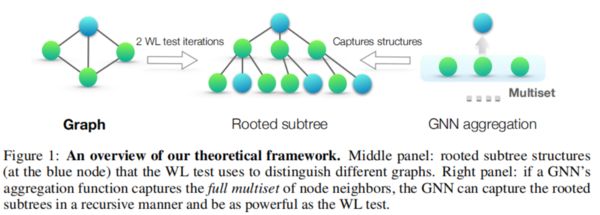 概览
概览
因此,WL子树核算法考虑的图特征本质上图的不同子树的数量。
三、理论框架
如上面显示的,GNN递归地更新节点的特征来捕获网络的结构和其邻域节点的特征,也就是其对应的子树结构。在本文中我们首先假设节点的输入特征都来自一个可数的全集,对于有限图来说,节点在任何固定模型的深层特征向量也来自一个可数的全集。为了标记的简便性,我们为每个特征向量设置一个单独的标签。如此的话节点的邻域节点集合就组成了一个multiset:同一个元素可以出现多次,也就是说不同的节点能够拥有相同的特征向量。
「定义1.」 一个multiset是一个允许元素出现多次的set,形式化的来描述,一个multiset是一个元组,是底层的集合,由不同的元素组成,定义了元素的多样性。
为了探索GNN的表征能力,我们分析什么时候GNN会将两个几点映射到embedding空间的同一位置。直观地来看,一个拥有最大化表征能力的GNN仅在两个节点拥有相同的子树结构以及对应节点相同的特征时,会将这两个节点的embedding映射到同一位置。因为子树结构由节点邻域递归地定义,因此我们可以将对上述问题的分析退化成一个GNN是否将两个邻域(也就是两个multiset)映射到相同的embedding或者表示。一个最大表征能力的GNN绝不会将两个不同的邻域映射到相同的表示,这意味着其聚合的模式一定是单射的。因此,我们将GNN的聚合模式抽象成一个其神经网络能表示的multiset上的函数,并且分析它们是否能够表示单射multiset函数。
四、构建强表征能力的GNN
如前所述,一个最大化表征能力的GNN能够将同构图映射到相同的表示,将非同构图映射到不同的表示,然而,这意味着GNN能够解决图同构问题,这是很困难的。因而在本文的分析中对GNN的表征能力的上限进行了放缩,以WL图同构测试这个启发式的方法作为GNN表征容量的标准,其在大多数条件下效果很好,而在某些情况下效果不佳,比如正则图。
「引理2.」 和表示任意两个非同构图,如果一个图神经网络将和映射到不同的embedding,那么WL图同构测试也会任务这两个图是非同构的。
本文所有的理论都在附录中有证明。由上述引理可以推断出任何基于聚合的GNN至多与WL测试具备同样的表征能力,也就是说WL测试是其上限。那么现在问题是是否存在GNN在原则上与WL测试性能相当呢?定理3告诉我们是存在的,只需要GNN的聚合函数和readout函数是单射的。
「定理3.」 一个图神经网络在满足下列条件时能够将WL测试认为是非同构图的两个图和映射到不同的embedding:
①按照下面的方式迭代聚合和更新节点特征:
❝ ❞
这里的multiset上的函数以及是单射的。
②的图级readout函数(在节点特征的multiset上进行操作)是单射的。
对于可数集,单射性很好地刻画了函数是否保持输入的特殊性。对于不可数集,节点特征是连续的情况,需要一些其他的条件。本文只讨论可数集上的特征。
「引理4.」 假设输入特征空间是可数的,代表GNN的第层函数,,定义在大小有界的multiset上,的只与,也就是节点隐藏特征也是可数的。
值得一提的是,GNN除了区分不同的图以外,还有一个重要的优点是能够捕获图结构的相似性。注意在WL测试中的节点特征本质上是one-hot编码,因此不能捕获子树之间的相似性。相应的,满足定理3中标准的GNN能够学习将子树嵌入到低维空间,这相当于推广了WL测试。这使得GNN不仅能够区分不同的结构,而且能够学习将相似的图结构映射到相似的embedding,并捕获图结构之间的依赖关系。捕捉节点标签的结构相似性对泛化是有帮助的,特别是当不同图上的子树共现很少或有噪声边和节点特征时。
图同构网络(GIN)
为了能够建模用于聚合的单射multiset函数,本文发明了“deep multisets”的理论,也就是用神经网络来参数化通用multiset函数。下面的引理阐述了sum聚合函数能够表示单射的通用multiset函数。
「引理5.」 假设是可数的,存在一个函数以便于对于每一个大小有界的multiset都是不同的。进一步来讲,任意multiset函数都可以被分解成关于某个函数的。
Deep multiset和set的一个重要区别是一些热门的set上的单射函数对于multiset来说不是单射的,比如mean聚合函数。依照上面的引理,本文设计了一种简单而具体的聚合方案,也就是下面的推论。
「推论6.」 假设是可数的,存在一个函数使得对于的无限个选择,包括所有的无理数,有对于每个对都是不同的,这里的且,是一个大小有界的multiset。进一步来讲,任意在这样的对上的函数都可以被分解成关于某函数的。
我们可以采用MLP来建模和学习与。在实际应用中,我们采用一个MLP来建模,这是因为MLP可以表示函数的组合。在第一次迭代时,如果节点输入特征是one-hot向量则在相加前不需要MLP,这是因为仅仅相加也可以保证单射。可以是一个可学习的参数,也可以是一个固定的值。最终,GIN更新节点特征的模式如下:
❝ ❞
GIN的图级readout函数
需要注意的是,随着迭代次数的增加,对应于子树结构的节点表示会变得更加精细和全局。足够的迭代次数是获得良好鉴别能力的关键。然而,来自早期迭代的特性有时泛化地更好。为了考虑所有的结构信息,我们使用来自模型所有深度的信息:
❝ ❞
根据定理3和推论6,GIN可以使用sum来作为函数。
五、对其他GNN的分析
该部分研究了GCN和GraphSAGE的设计,其均不满足定理3中的条件。本文进行了聚合函数的消融实验,包括:
①一层感知机而非MLP;
②mean或者max-pooling。
我们将看到,这些GNN变体会对非常简单的图识别困难,并且没有WL测试那么优越。尽管如此,具有像GCN这样的mean聚合函数的模型对于节点分类任务表现良好。为了更好的理解这些现象,本文做了以下研究。
一层感知机是不够充分的
一些GNN采用一层感知机来作为引理5中的,这样的一层映射是广义线性模型的例子。下面的引理说明了一层感知机是不够充分的。
「引理7.」 存在有限的multiset使得对于任意的线性映射有。
引理7证明的主要思想是一层感知器的行为很像线性映射,因此GNN层退化为简单的对邻域特征求和。在线性映射中缺少偏置项,如果加上偏置并且有足够大的输出维度,一层感知机或许能够区分不同的multiset。尽管如此,与使用MLP的模型不同,1层感知器(即使有偏置项)也不是multiset函数的通用近似器。因此,即使具有一层感知器的GNN可以在一定程度上将不同的图嵌入到不同的位置,这种嵌入可能不能充分地捕获结构相似性,并且对于简单的分类器,如线性分类器,很难拟合。
Mean或者max-pooling难以识别的结构
如果替换中的sum为mean或者max-pooling。下图为三种聚合函数的表征能力进行了排名:
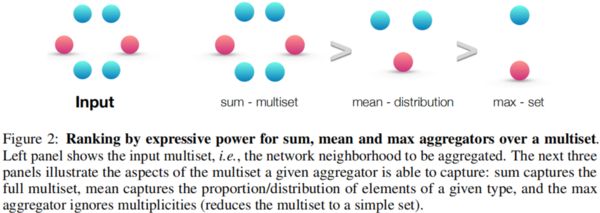 排名
排名
下图展示了mean和max聚合函数不能识别的结构,如果将两个不同结构聚合后得到相同的表示,则认为该种聚合函数是失败的:
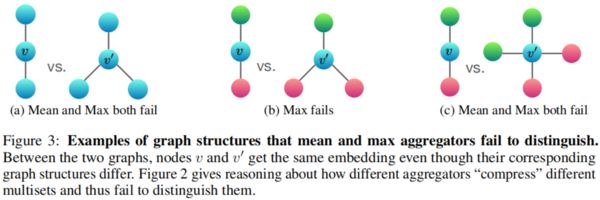 举例
举例
Mean聚合函数学习分布
考虑和,mean聚合函数会将这两个multiset聚合得到相同的表示,因此mean聚合函数学习到的是multiset中元素的分布(或者说比例)。
「推论8.」 假设是可数的,存在一个函数使得对于,当且仅当multiset和具备同样的分布时有。也就是说假设,那么有和,这里的。
对于任务来说,如果图中的统计信息和分布信息比精确结构更重要,则mean聚合函数可以有很好的性能。此外,当节点特征多样且很少重复时,mean聚合函数与sum聚合函数性能相当。具有mean聚合函数的GNN对于文章主题分类和社区检测等节点分类任务是有效的,这些任务节点特征丰富,邻域特征的分布为任务提供了强信号。
Max聚合函数学习具有显著元素的set
上面的图显示max聚合函数将具有相同特性的多个节点视为只有一个节点,也就是将multiset看做set。Max聚合函数既不识别精确结构也不识别分布,然而,它可能适合于识别具有代表性的元素或“骨架”。之前的研究表明,max聚合函数能够识别一个3D点云的骨架,并且对噪声和离群值有一定的健壮性。下面的推论表明,max聚合函数捕获了multiset底层的set。
「推论9.」 假设是可数的,存在一个函数使得对于,当且仅当multiset和具备同样的底层set时有。
本文只分析了mean和max-pooling两种聚合方法,还有一些其他的如通过注意力加权平均的方法或者LSTM pooling等。本文的理论框架足够通用,可以用于分析任何基于聚合的GNN的表征能力。
六、实验
训练集效果
训练集效果代表了模型的表征能力上限:
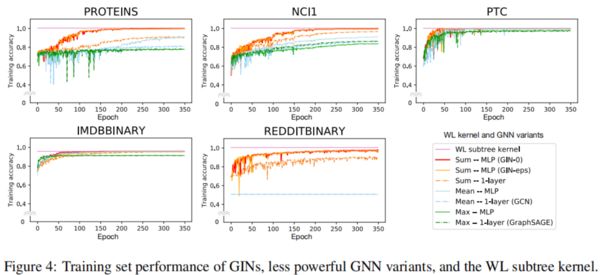 训练集
训练集
测试集效果
测试集效果验证模型的泛化能力:
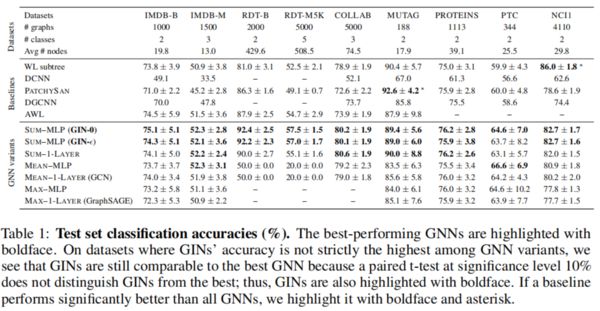 测试集
测试集