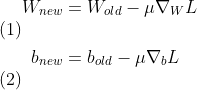CS231n-2022 Module1: Minimal Neural Network case study

目录

1. 前言

2. 数据生成

3. 训练一个Softmax线性分类器

3.1 参数初始化

3.2 计算分类分数（class scores）

3.3 计算分类概率

3.4 计算交叉熵损失函数

3.5 基于反向传播计算解析梯度（analytic gradient）

3.6 参数更新

3.7 组装到一起进行训练

3.7.1 处理框图

3.7.2 代码

4. 训练一个神经网络

---

1. 前言

         本文编译自斯坦福大学的CS231n课程（2022） Module1课程中神经网络部分之一，原课件网页参见：

        CS231n Convolutional Neural Networks for Visual Recognition
        本文（本系列）不是对原始课件网页内容的完全忠实翻译，只是作为学习笔记的摘要，主要是自我参考，而且也可能夹带一些私货（自己的理解和延申，不保证准确性）。如果想要更准确地了解更具体的细节，还请服用原文。如果本摘要恰巧也对小伙伴们有所参考则纯属无心插柳概不认账^-^。       

        前面几篇：

        CS231n-2022 Module1: 神经网络1：Setting Up the Architecture

        CS231n-2022 Module1: 神经网络2

        CS231n-2022 Module1: 神经网络3：Learning and Evaluation

2. 数据生成

        本实验的目的是通过对比来体现深度神经网络（当然本实验中其实只是有一个隐藏层，即2层神经网络）相对于浅层网络（没有隐藏层，比如说线性分类器，可以看作1层神经网络）的优势，所以我们需要一个线性不可分的数据集，线性分类器无法正确分类，而2层神经网络则能够进行正确分类（具体情况取决于分类问题本身的难易度）。

        一般来说我们需要对数据做归一化预处理（比如说，使得数据集的每个feature都变成零均值、单位标准偏差），但是以上玩具数据集的范围已经在[-1, 1]范围内，所以我们可以跳过这一步。

        在scikit-learn库中给出了一些常用（玩具）数据集的获取或者生成方法，有兴趣者可以参考：

                机器学习笔记：常用数据集之scikit-learn生成分类和聚类数据集

3. 训练一个Softmax线性分类器

        正如把大象装到冰箱里需要三步一样，训练一个机器学习模型也由基本固定的套路，以下分步骤说明。对应代码参考最后的3.7中的代码中对应章节号部分。

3.1 参数初始化

        本Softmax分类器的参数包括权重参数W和偏置参数b。

        W通常用零均值、小方差的高斯分布进行初始化，而b则初始化为全0即可。

3.2 计算分类分数（class scores）

                

        张量下标中的“[]”用于表示张量的维度，以下同。

3.3 计算分类概率

        基于softmax函数将scores变换成对应于各class#k的概率：

                

3.4 计算交叉熵损失函数

        Softmax分类器使用的损失函数为交叉熵损失函数（softmax loss, cross-entropy loss）。给定一个分布P和一个分布Q，交叉熵定义为([1])：

                

        其中，P(x)代表在分布P中x发生的概率，Q(x)代表在分布Q中x发生的概率。

        以P代表真值的分布，显然应该是一个one-hot的分布。比如说在本例中有三种分类{0，1，2}，假设样本xi的真值yi = 1，则应该有。

        以Q代表预测值的分布，即Q = [probs[0],probs[1],probs[2]].

        则显而易见的是，样本i {xi, yi}的损失应该为：                        

                

        而整个数据集的总（平均）损失自然应该是：

                

        进一步，还要加上正则化损失（这里考虑正则化损失）得到：

                

        其中，正则化损失的系数（1/2)仅仅是为了数学推导的方便（平方项求导后会产生2的因子，两者抵消会显得梯度的解析式更清爽一些）。

        正则化系数作为模型的一个超参数进行调节。

        如上一篇所述，作为梯度检查的一项，在正则化系数置0，随机初始化后，loss的初始值应该为（注意，本文中log均指自然对数，即ln()）。可以据此判断loss的实现是否存在明显的错误。

3.5 基于反向传播计算解析梯度（analytic gradient）

        上面我们已经得到了损失函数，神经网络训练的目的就是要使损失最小化。我们将采用梯度下降（gradient descent）方法。基本思路是，从随机参数出发，计算损失函数关于这些参数的梯度，并由此确定向哪个方向以多大步长进行参数调节。

        为了简洁起见，重写一下分类概率和样本损失（scores --> f, probs --> p, []-->下标），并推导（单个样本的损失关于分类k的分数的）偏导数如下（其中关键是求导的链式法则。偏导数是构成梯度的元素）： 

        注意，以上推导是针对 的，所以，其中f应该视为关于样本{i}的。所以，应该写作(即样本i的识别为分类k的分数)，应该写做，应该写成。。。

        其中，I(x)表示Indicator function，也有写做1(x)的。softmax之所以令人喜欢就在于它所导致的梯度是如此简洁优雅（其根源又在于指数函数的魔力）。下面通过一个简单的例子来增进直观的理解。假设针对样本通过计算得到​​​​​p = [0.2, 0.3, 0.5], 并且假定正确的分类是k=1(中间那个，其概率为0.3)。根据以上梯度公式可以得到（这里为简洁起见，以df表示梯度向量） df = [0.2, -0.7, 0.5]。由于正确的分类是k=1，因此如果增大p[0]或者p[2]，应该会导致loss变大，df[0]和df[2]大于0正好与此相符，同理如果增大p[1]则应该会导致loss变小，这对应着df[1]=-0.7<0。

          有了后，就可以进一步基于反向传播、链式法则，求得loss关于W、b的梯度。以下仅给出loss对于某个权重参数的偏微分作为示例（由此扩充至以及是一个顺理成章水到渠成的过程）：

                

         以, 分别代表整个数据集的scores = np.dot(X, W) + b和概率矩阵，则基于以上推导经过一些矩阵微积分（matrix calculus）运算可以得到：

        ​​​​​​​                         

        同理可以得到总体损失关于向量b的梯度（但是其表达式稍微有点难写）。 

        由此可以得到以下梯度计算的实现代码。注意梯度计算的实现代码中的对应关系：probs--; dscores--（加转置是为了维度匹配），dW和db分别表示loss关于W和b的梯度（最后还加上正则化损失部分的梯度）：  

dscores = probs
dscores[range(num_examples),y] -= 1
dscores /= num_examples

dW = np.dot(X.T, dscores)
db = np.sum(dscores, axis=0, keepdims=True)
dW += reg*W # don't forget the regularization gradient

        注意正则化梯度（ regularization gradient）的形式非常简单 reg*W ，这是因为，正如前面我们提到过，正则化损失中有个1/2的因子恰好被平方项的导数产生的因子2抵消了.

3.6 参数更新

        有了梯度和和另一个超参数(step_size)，参数的更新就直截了当了：

        ​​​​​​​        

3.7 组装到一起进行训练

3.7.1 处理框图

        将以上所有要素组装到一起，就得到了一个Softmax分类器，处理框图示意如下：

        由以上框图可以看出， loss函数本身其实只是用于训练进度状况监测用的。训练（学习）本身并不要求显式地计算loss，而是跳过loss直接计算梯度了。

3.7.2 代码

        基本上是原课件代码（网页内嵌代码以及minimal_net.ipynb），稍微有一些调整和修改（比如说python2-->python3的相关修改）、注释，在JupyterNotebook中运行验证过。

# A bit of setup
import numpy as np
import matplotlib.pyplot as plt

%matplotlib inline
plt.rcParams['figure.figsize'] = (10.0, 8.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'

# for auto-reloading extenrnal modules
# see http://stackoverflow.com/questions/1907993/autoreload-of-modules-in-ipython
%load_ext autoreload
%autoreload 2

# 2.数据生成
M = 100 # number of points per class。原示例中用N，容易混淆。通常用N表示数据集总的样本数。
D = 2   # dimensionality
K = 3   # number of classes
N = M*K # 总样本数
X = np.zeros((N,D)) # data matrix (each row = single example)
y = np.zeros(N, dtype='uint8') # class labels
for j in range(K):
  ix = range(M*j,M*(j+1))
  r = np.linspace(0.0,1,M) # radius
  t = np.linspace(j*4,(j+1)*4,M) + np.random.randn(M)*0.2 # theta
  X[ix] = np.c_[r*np.sin(t), r*np.cos(t)]
  y[ix] = j
# lets visualize the data:
plt.scatter(X[:, 0], X[:, 1], c=y, s=40, cmap=plt.cm.Spectral)
plt.show()

# 3.0 some hyperparameters
step_size = 1e-0
reg = 1e-3 # regularization strength

# 3.1 initialize parameters randomly
W = 0.01 * np.random.randn(D,K)
b = np.zeros((1,K))

# gradient descent loop
num_examples = X.shape[0]
for i in range(200): # Each iteration corresponding to one epoch.
  # 3.2 evaluate class scores, [N x K]
  scores = np.dot(X, W) + b

  # 3.3 compute the class probabilities
  exp_scores = np.exp(scores)
  probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True) # [N x K]

  # 3.4 compute the loss: average cross-entropy loss and regularization
  correct_logprobs = -np.log(probs[range(num_examples),y])
  data_loss = np.sum(correct_logprobs)/num_examples
  reg_loss = 0.5*reg*np.sum(W*W)
  loss = data_loss + reg_loss
  if i % 10 == 0:
    print("iteration %d: loss %f" % (i, loss)) 

  # 3.5 compute the gradient on scores
  dscores = probs
  dscores[range(num_examples),y] -= 1
  dscores /= num_examples

  # backpropate the gradient to the parameters (W,b)
  dW = np.dot(X.T, dscores)
  db = np.sum(dscores, axis=0, keepdims=True)

  dW += reg*W # regularization gradient

  # perform a parameter update
  W += -step_size * dW
  b += -step_size * db

# evaluate training set accuracy
scores = np.dot(X, W) + b
predicted_class = np.argmax(scores, axis=1)
print ('training accuracy: %.2f' % (np.mean(predicted_class == y)))

运行结果如下： 

 。。。

iteration 170: loss 0.785329
iteration 180: loss 0.785282
iteration 190: loss 0.785249

training accuracy: 0.52

        50%的准确度当然不能说好，但是考虑到数据集本来是非线性可分的，现在强行用一个线性分类器来分类，结果不好也是意料之内的事情。为了更直观地看到训练效果，用以下代码将所训练好的分类器的分类边界画出来，如下所示：

# plot the resulting classifier
h = 0.02
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
                     np.arange(y_min, y_max, h))
Z = np.dot(np.c_[xx.ravel(), yy.ravel()], W) + b
Z = np.argmax(Z, axis=1)
Z = Z.reshape(xx.shape)
fig = plt.figure()
plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral, alpha=0.8)
plt.scatter(X[:, 0], X[:, 1], c=y, s=40, cmap=plt.cm.Spectral)
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
#fig.savefig('spiral_linear.png')

        如上图所示，分类判决边界为直线，这正是线性分类器的特征。

        下一节我们来针对以上模型追加一级隐藏层，使其从浅层（线性）网络变成深层（非线性） 网络，见识一下由于非线性带来的深度神经网络的威力。

 

4. 训练一个神经网络

        未完待续

参考文献：

[1] https://machinelearningmastery.com/cross-entropy-for-machine-learning