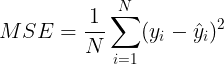机器学习（8）sklearn画决策树（回归树）

目录

一、DecisionTreeRegressor

1、criterion

2、接口

3、交叉验证

二、用sklearn画回归树（基于波士顿房价训练模型）

1、导入库

2、训练模型

3、用Graphviz画回归树

 三、回归树对正弦函数上的噪音点降噪

1、导入库

2、生成带噪音点的正弦函数

3、训练模型

4、画plt图

---

一、DecisionTreeRegressor

sklearn.tree._classes.DecisionTreeRegressor

def __init__(self,
             *,
             criterion: Any = "squared_error",
             splitter: Any = "best",
             max_depth: Any = None,
             min_samples_split: Any = 2,
             min_samples_leaf: Any = 1,
             min_weight_fraction_leaf: Any = 0.0,
             max_features: Any = None,
             random_state: Any = None,
             max_leaf_nodes: Any = None,
             min_impurity_decrease: Any = 0.0,
             ccp_alpha: Any = 0.0) -> None

1、criterion

        criterion作为回归树的衡量分枝的指标，也是衡量回归树回归质量的指标，有三种标准：

（1）“mse”:均方误差，父节点和叶子节点之间的均方误差的差额来作为特征选择的标准，这种方法通过叶子节点的的均值来最小化L2损失

（2）“friedman_mse”：费尔德曼均方误差，针对潜在分枝问题改进后的均方误差

（3）“mae”:绝对平均误差，这种方法通过使用叶子节点的中值来最小化L1损失

         计算机中默认用负均方误差（neg_mean_squared_error）来进行运算与存储。

2、接口

        回归树中的重要接口仍然是apply，fit，score，predict，feature_importance_。

        但是score返回的是R^2，即相关系数，而非MSE。

        可以通过参数scoring来指定负均方误差返回。

score=cross_val_score(dtg
                      ,boston.data
                      ,boston.target
                      ,cv=10
                      ,scoring='neg_mean_squared_error')

3、交叉验证

        交叉验证：通过将数据划分为n份，依次使用其中一份作为测试集，其他n-1份作为训练集，多次计算模型的精确性来评估模型的平均准确程度。由于训练集和测试集的划分会存在干扰模型的结果，因此多次进行交叉验证来求出平均值，能提升模型准确率。

二、用sklearn画回归树（基于波士顿房价训练模型）

1、导入库

from sklearn.datasets import load_boston                #导入波士顿房价数据集
from sklearn.model_selection import cross_val_score     #交叉验证函数
from sklearn.tree import DecisionTreeRegressor          #回归树
from sklearn import tree                                #导入tree

2、训练模型

boston=load_boston()
dtg=DecisionTreeRegressor(random_state=0)             #criterion默认为MSE
score=cross_val_score(dtg                             #十次交叉验证
                        ,boston.data
                        ,boston.target
                        ,cv=10
                        ,scoring='neg_mean_squared_error')

print(score)                                          #输出负均方误差

3、用Graphviz画回归树

import graphviz                            #导入graphviz库
feature_names=boston.feature_names         #标签使用boston房价特征
data_graph=tree.export_graphviz(dtg.fit(boston.data,boston.target)  #第一个参数是训练好的模型，不是回归树类
                                ,feature_names=feature_names
                                ,filled=True
                                ,rounded=True)
graph=graphviz.Source(data_graph)
graph.view()

        回归树的图太庞大的，不便在此处演示。

 三、回归树对正弦函数上的噪音点降噪

1、导入库

from sklearn.tree import DecisionTreeRegressor
import matplotlib.pyplot as plt
import numpy as np

2、生成带噪音点的正弦函数

rng=np.random.RandomState(1)            #随机数种子
x=np.sort(10*rng.rand(80,1),axis=0)     #生成0-10之间随机数x取值
y=np.sin(x).ravel()                     #生成正弦曲线y值
y[::5]+=1*(0.5-rng.rand(16))            #正弦函数上每过五个点生成一个随机噪音，共16个点

3、训练模型

regr_1=DecisionTreeRegressor(max_depth=5)            #分别生成深度为5和8的回归树
regr_2=DecisionTreeRegressor(max_depth=8)            
regr_1=regr_1.fit(x,y)                               #训练模型
regr_2=regr_2.fit(x,y)

4、画plt图

x_test=np.arange(0,10,0.01)[:,np.newaxis]             #对x_test进行升维，其中':'在的位置为原始维度，np.newaxis为补充维度
y_1=regr_1.predict(x_test)
y_2=regr_2.predict(x_test)

plt.figure()                                          #展开画布
plt.scatter(x,y,s=20,color='r')
plt.plot(x_test,y_1,color='b',label='max_depth=5')
plt.plot(x_test,y_2,color='g',label='max_depth=8')    #过拟合
plt.legend()                                          #坐标显示
plt.show()

         从图中可以看出max_depth=8时，过于依赖数据（包括噪音点），造成过拟合。