机器学习实战 —— 决策树
代码
"""
用字典存储决策树结构:
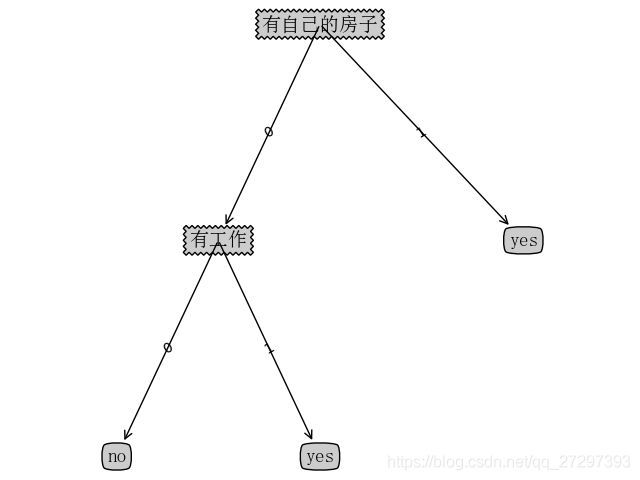
{'有自己的房子':{0:{'有工作':{0:'no', 1:'yes'}}, 1:'yes'}}
年龄:0代表青年,1代表中年,2代表老年
有工作:0代表否,1代表是
有自己的房子:0代表否,1代表是
信贷情况:0代表一般,1代表好,2代表非常好
类别(是否给贷款):no代表否,yes代表是
pickle包可以将决策树保存下来,方便下次直接调用
"""
from matplotlib.font_manager import FontProperties
import matplotlib.pyplot as plt
from math import log
import operator
import pickle
def createDataSet():
"""
函数说明:创建测试数据集;《统计学习方法》第二版的P71中表5.1的数据
Parameters:
None
Returns:
dataSet - 数据集
labels - 各列特征的标签
"""
# 数据集
dataSet = [[0, 0, 0, 0, 'no'],
[0, 0, 0, 1, 'no'],
[0, 1, 0, 1, 'yes'],
[0, 1, 1, 0, 'yes'],
[0, 0, 0, 0, 'no'],
[1, 0, 0, 0, 'no'],
[1, 0, 0, 1, 'no'],
[1, 1, 1, 1, 'yes'],
[1, 0, 1, 2, 'yes'],
[1, 0, 1, 2, 'yes'],
[2, 0, 1, 2, 'yes'],
[2, 0, 1, 1, 'yes'],
[2, 1, 0, 1, 'yes'],
[2, 1, 0, 2, 'yes'],
[2, 0, 0, 0, 'no']]
# 各列特征的标签
labels = ['年龄', '有工作', '有自己的房子', '信贷情况']
# 返回数据集及各列特征的标签
return dataSet, labels
def calcShannonEnt(dataSet):
"""
函数说明:计算给定数据集的经验熵(香农熵)
Ent = -SUM(prob*Log2(prob))
Parameters:
dataSet - 数据集
Returns:
shannonEnt - 经验熵(香农熵)
"""
# 返回数据集的行数
numEntires = len(dataSet)
# 构建标签(Label)计数的字典
labelCounts = {}
# 对每组特征向量进行统计
for featVec in dataSet:
# 提取标签(Label)信息
currentLabel = featVec[-1]
# 如果标签(Label)没有放入统计次数的字典,添加进去
if currentLabel not in labelCounts.keys():
# 创建一个新的键值对,键为currentLabel值为0
labelCounts[currentLabel] = 0
# Label计数
labelCounts[currentLabel] += 1
# 经验熵(香农熵)
shannonEnt = 0.0
# 计算香农熵
for key in labelCounts:
# 选择该标签(Label)的概率
prob = float(labelCounts[key]) / numEntires
# 利用公式计算
shannonEnt -= prob*log(prob, 2)
# 返回经验熵(香农熵)
return shannonEnt
def splitDataSet(dataSet, axis, value):
"""
函数说明:按照指定特征的值划分数据集
Parameters:
dataSet - 待划分的数据集
axis - 指定划分数据集的特征
values - 指定特征的值划
Returns:
retDataSet - 按照
"""
# 创建返回的数据集列表
retDataSet = []
# 遍历数据集的每一行
for featVec in dataSet:
if featVec[axis] == value:
# 去掉axis特征列
reducedFeatVec = featVec[:axis]
# extend() 函数用于在列表末尾一次性追加另一个序列中的多个值(用新列表扩展原来的列表)。
reducedFeatVec.extend(featVec[axis+1:])
# 将划分后的数据添加到数据集
retDataSet.append(reducedFeatVec)
# 返回划分后的数据集
return retDataSet
def chooseBestFeatureToSplit(dataSet):
"""
核心算法:
ID3:选取信息增益最大的特征(此函数用的算法)
C4.5:选取信息增益比最大的特征
函数说明:选择最优特征
Gain(D,g) = Ent(D) - SUM(|Dv|/|D|)*Ent(Dv)
Parameters:
dataSet - 数据集
Returns:
bestFeature - 信息增益最大的(最优)特征的索引值
"""
# 特征数量
numFeatures = len(dataSet[0]) - 1
# 计算数据集的香农熵
baseEntropy = calcShannonEnt(dataSet)
# 信息增益
bestInfoGain = 0.0
# 最优特征的索引值
bestFeature = -1
# 遍历数据集中各列特征
for i in range(numFeatures):
# 获取dataSet中第i个所有特征值,存放在featList列表中(列表生成式)
featList = [example[i] for example in dataSet]
# 创建set集合{},元素不可重复,重复的元素均被删掉
uniqueVals = set(featList)
# 经验条件熵
newEntropy = 0.0
# 计算信息增益
for value in uniqueVals:
# subDataSet为按照指定特征列给定的特征值进行划分后的子集
subDataSet = splitDataSet(dataSet, i, value)
# 计算子集的概率
prob = len(subDataSet) / float(len(dataSet))
# 根据公式计算经验条件熵
newEntropy += prob * calcShannonEnt(subDataSet)
# 信息增益
infoGain = baseEntropy - newEntropy
# 打印每个特征的信息增益
print("第%d个特征的增益为%.3f" % (i, infoGain))
# 计算信息增益
if(infoGain > bestInfoGain):
# 更新信息增益,找到最大的信息增益
bestInfoGain = infoGain
# 记录信息增益最大的特征的索引值
bestFeature = i
# 返回信息增益最大的特征的索引值
return bestFeature
def majorityCnt(classList):
"""
函数说明:统计classList中出现次数最多的元素(类标签)
服务于递归的第2个终止条件
Parameters:
classList - 类标签列表
Returns:
sortedClassCount[0][0] - 出现次数最多的元素(类标签)
"""
classCount = {}
# 统计classList中每个元素出现的次数
for vote in classList:
if vote not in classCount.keys():
classCount[vote] = 0
classCount[vote] += 1
# 根据字典的值降序排序
# operator.itemgetter(1)获取对象的第1列的值
sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)
# 返回classList中出现次数最多的元素
return sortedClassCount[0][0]
def createTree(dataSet, labels, featLabels):
"""
函数说明:创建决策树(ID3算法)
递归有两个终止条件:1、所有的类标签完全相同,直接返回类标签
2、用完所有标签但是得不到唯一类别的分组,即特征不够用,挑选出现数量最多的类别作为返回
Parameters:
dataSet - 训练数据集
labels - 分类属性标签
featLabels - 存储选择的最优特征标签
Returns:
myTree - 决策树
"""
# 取分类标签(是否放贷:yes or no)
classList = [example[-1] for example in dataSet]
# 递归终止条件1:如果类别完全相同则停止继续划分
if classList.count(classList[0]) == len(classList):
return classList[0]
# 递归终止条件2:遍历完所有特征时返回出现次数最多的类标签
if len(dataSet[0]) == 1:
return majorityCnt(classList)
# 选择最优特征,
bestFeat = chooseBestFeatureToSplit(dataSet)
# 最优特征的标签
bestFeatLabel = labels[bestFeat]
featLabels.append(bestFeatLabel)
# 根据最优特征的标签生成树
myTree = {bestFeatLabel: {}}
# 删除已经使用的特征标签
del(labels[bestFeat])
# 得到训练集中所有最优解特征的属性值
featValues = [example[bestFeat] for example in dataSet]
# 去掉重复的属性值
uniqueVals = set(featValues)
# 遍历特征,创建决策树
for value in uniqueVals:
myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), labels, featLabels)
return myTree
def getNumLeafs(myTree):
"""
函数说明:获取决策树叶子结点的数目
Parameters:
myTree - 决策树
Returns:
numLeafs - 决策树的叶子结点的数目
"""
# 初始化叶子
numLeafs = 0
# python3中myTree.keys()返回的是dict_keys,不是list,所以不能用
# myTree.keys()[0]的方法获取结点属性,可以使用list(myTree.keys())[0]
# next() 返回迭代器的下一个项目 next(iterator[, default])
firstStr = next(iter(myTree))
# 获取下一组字典
secondDict = myTree[firstStr]
for key in secondDict.keys():
# 测试该结点是否为字典,如果不是字典,代表此节点为叶子结点
if type(secondDict[key]).__name__ == 'dict':
numLeafs += getNumLeafs(secondDict[key])
else:
numLeafs += 1
return numLeafs
def getTreeDepth(myTree):
"""
函数说明:获取决策树的层数
Parameters:
myTree - 决策树
Returns:
maxDepth - 决策树的层数
"""
# 初始化决策树深度
maxDepth = 0
# python3中myTree.keys()返回的是dict_keys,不是list,所以不能用
# myTree.keys()[0]的方法获取结点属性,可以使用list(myTree.keys())[0]
# next() 返回迭代器的下一个项目 next(iterator[, default])
firstStr = next(iter(myTree))
# 获取下一个字典
secondDict = myTree[firstStr]
for key in secondDict.keys():
# 测试该结点是否为字典,如果不是字典,代表此节点为叶子结点
if type(secondDict[key]).__name__ == 'dict':
thisDepth = 1 + getTreeDepth(secondDict[key])
else:
thisDepth = 1
# 更新最深层数
if thisDepth > maxDepth:
maxDepth = thisDepth
# 返回决策树的层数
return maxDepth
def plotNode(nodeTxt, centerPt, parentPt, nodeType):
"""
函数说明:绘制结点
Parameters:
nodeTxt - 结点名
centerPt - 文本位置
parentPt - 标注的箭头位置
nodeType - 结点格式
Returns:
None
"""
# 定义箭头格式
arrow_args = dict(arrowstyle="<-")
# 设置中文字体
font = FontProperties(fname=r"C:\Windows\Fonts\simsun.ttc", size=14)
# 绘制结点createPlot.ax1创建绘图区
# annotate是关于一个数据点的文本
# nodeTxt为要显示的文本,centerPt为文本的中心点,箭头所在的点,parentPt为指向文本的点
createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction',
xytext=centerPt, textcoords='axes fraction',
va='center', ha='center', bbox=nodeType,
arrowprops=arrow_args, FontProperties=font)
def plotMidText(cntrPt, parentPt, txtString):
"""
函数说明:标注有向边属性值
Parameters:
cntrPt、parentPt - 用于计算标注位置
txtString - 标注内容
Returns:
None
"""
# 计算标注位置(箭头起始位置的中点处)
xMid = (parentPt[0]-cntrPt[0])/2.0 + cntrPt[0]
yMid = (parentPt[1]-cntrPt[1])/2.0 + cntrPt[1]
createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", rotation=30)
def plotTree(myTree, parentPt, nodeTxt):
"""
函数说明:绘制决策树
Parameters:
myTree - 决策树(字典)
parentPt - 标注的内容
nodeTxt - 结点名
Returns:
None
"""
# 设置结点格式boxstyle为文本框的类型,sawtooth是锯齿形,fc是边框线粗细
decisionNode = dict(boxstyle="sawtooth", fc="0.8")
# 设置叶结点格式
leafNode = dict(boxstyle="round4", fc="0.8")
# 获取决策树叶结点数目,决定了树的宽度
numLeafs = getNumLeafs(myTree)
# 获取决策树层数
depth = getTreeDepth(myTree)
# 下个字典
firstStr = next(iter(myTree))
# 中心位置
cntrPt = (plotTree.xoff + (1.0 + float(numLeafs)) / 2.0 / plotTree.totalW, plotTree.yoff)
# 标注有向边属性值
plotMidText(cntrPt, parentPt, nodeTxt)
# 绘制结点
plotNode(firstStr, cntrPt, parentPt, decisionNode)
# 下一个字典,也就是继续绘制结点
secondDict = myTree[firstStr]
# y偏移
plotTree.yoff = plotTree.yoff - 1.0 / plotTree.totalD
for key in secondDict.keys():
# 测试该结点是否为字典,如果不是字典,代表此结点为叶子结点
if type(secondDict[key]).__name__ == 'dict':
# 不是叶结点,递归调用继续绘制
plotTree(secondDict[key], cntrPt, str(key))
# 如果是叶结点,绘制叶结点,并标注有向边属性值
else:
plotTree.xoff = plotTree.xoff + 1.0 / plotTree.totalW
plotNode(secondDict[key], (plotTree.xoff, plotTree.yoff), cntrPt, leafNode)
plotMidText((plotTree.xoff, plotTree.yoff), cntrPt, str(key))
plotTree.yoff = plotTree.yoff + 1.0 / plotTree.totalD
def createPlot(inTree):
"""
函数说明:创建绘图面板
Parameters:
inTree - 决策树(字典)
Returns:
None
"""
# 创建fig
fig = plt.figure(1, facecolor="white")
# 清空fig
fig.clf()
axprops = dict(xticks=[], yticks=[])
# 去掉x、y轴
createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)
# 获取决策树叶结点数目
plotTree.totalW = float(getNumLeafs(inTree))
# 获取决策树层数
plotTree.totalD = float(getTreeDepth(inTree))
# x偏移
plotTree.xoff = -0.5 / plotTree.totalW
plotTree.yoff = 1.0
# 绘制决策树
plotTree(inTree, (0.5, 1.0), '')
# 显示绘制结果
plt.show()
def classify(inputTree, featLabels, testVec):
"""
函数说明:使用决策树分类
Parameters:
inputTree - 已经生成的决策树
featLabels - 存储选择的最优特征标签
testVec - 测试数据列表,顺序对应最优特征标签
Returns:
classLabel - 分类结果
"""
# 获取决策树结点
firstStr = next(iter(inputTree))
# 下一个字典
secondDict = inputTree[firstStr]
featIndex = featLabels.index(firstStr)
for key in secondDict.keys():
if testVec[featIndex] == key:
if type(secondDict[key]).__name__ == 'dict':
classLabel = classify(secondDict[key], featLabels, testVec)
else:
classLabel = secondDict[key]
return classLabel
def storeTree(inputTree, filename):
"""
函数说明:存储决策树
Parameters:
inputTree - 已经生成的决策树
filename - 决策树的存储文件名
Returns:
None
"""
with open(filename, 'wb') as fw:
pickle.dump(inputTree, fw)
def grabTree(filename):
"""
函数说明:读取决策树
Parameters:
filename - 决策树的存储文件名
Returns:
pickle.load(fr) - 决策树字典
"""
fr = open(filename, 'rb')
return pickle.load(fr)
def main():
# 生成数据集及各列特征的标签
dataSet, labels = createDataSet()
# 创建featLabels:决策树最佳特征划分先后顺序的列表
featLabels = []
myTree = createTree(dataSet, labels, featLabels)
print("决策树最佳特征划分先后顺序的", featLabels)
# storeTree(myTree, 'classifierStorage.txt')
# myTree = grabTree('classifierStorage.txt')
# print(myTree)
# 测试数据
testVec = [0, 1, 1, 1]
result = classify(myTree, featLabels, testVec)
if result == 'yes':
print('放贷')
if result == 'no':
print('不放贷')
print(myTree)
createPlot(myTree)
# print(dataSet)
# print(calcShannonEnt(dataSet))
print("最优特征索引值:" + str(chooseBestFeatureToSplit(dataSet)))
if __name__ == '__main__':
main()
运行结果
第0个特征的增益为0.083
第1个特征的增益为0.324
第2个特征的增益为0.420
第3个特征的增益为0.363
第0个特征的增益为0.252
第1个特征的增益为0.918
第2个特征的增益为0.474
决策树最佳特征划分先后顺序的 ['有自己的房子', '有工作']
放贷
{'有自己的房子': {0: {'有工作': {0: 'no', 1: 'yes'}}, 1: 'yes'}}
第0个特征的增益为0.083
第1个特征的增益为0.324
第2个特征的增益为0.420
第3个特征的增益为0.363
最优特征索引值:2