单层感知器的原理及代码实现

 1.原理

1.1单层感知机的第一种表达形式

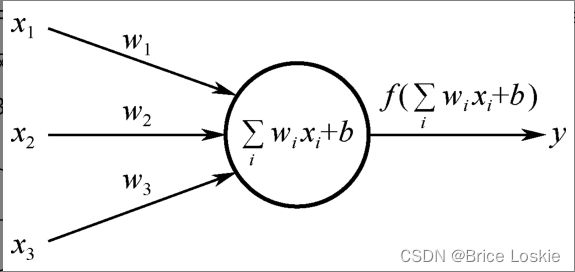
图为感知器的结构

 现在其中的数学符号做如下解释：

为输入信号。为的权值。

 表示细胞的输入信号在细胞核的位置进行汇总

b被称为偏置值，相当于神经元内部自带的信号。

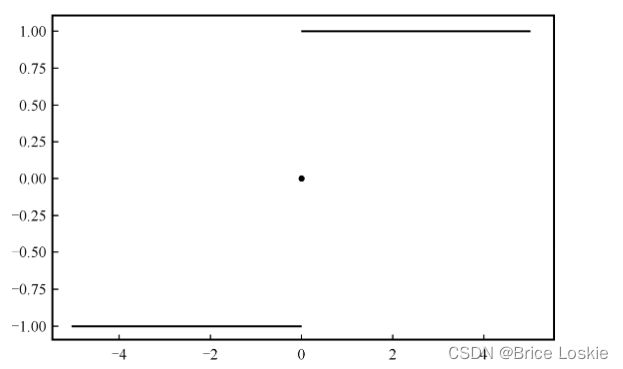
f（x）称为激活函数，理解为信号在轴突上进行的线性或非线性变化。在单层感知器中最开始使用的激活函数是sign（x）激活函数。该函数的特点是当x＞0时，输出值为1；当x=0时，输出值为0；当x＜0时，输出值为-1。函数如下图所示

 

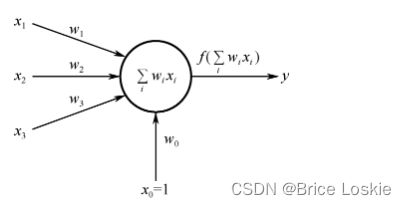
 1.2 单层感知机的另一种表达形式

即将b看作,且恒为1，原理和第一种形式相似，这里不再赘述

1.3 感知器的学习规则

 

 这是现在感知机的表达式

我们使用来对参数进行跟新

 Δwi表示第i个权值的变化，η表示学习率，；t是正确的标签（Target）。

因为单层感知器的激活函数为sign函数，所以t和y的取值都为±1。

这里举一个计算的实例(采用第二种感知机的表达式)：

=1 =0 =-1 =-5 =0 =0 学习率=1 正确的标签t=1  

我们采用代码完成感知器的学习：

1.数据准备

lr是指学习率

t是真实值

import numpy as np
x_0 = 1
x_1 = 0
x_2 = -1
w_0 = -5
w_1 = 0
w_2 = 0
t=1
lr = 1

2.模型算法

for i in range(100):
    y=np.sign(w_0*x_0+w_1*x_1+w_2*x_2)
    print("y:",y)
    if y!=t:
        w_0=w_0-lr*(y-t)*x_0
        w_1=w_1-lr*(y-t)*x_1
        w_2=w_2-lr*(y-t)*x_2
        print(w_0,w_1,w_2)
    else:
        break

代码运行结果如下：

y: -1
-3 0 -2
y: -1
-1 0 -4
y: 1

 最后更新之后的参数是 w_0 = -1,w_1 = 0, w_2=-4

3.也可以使用矩阵来做简单的感知机算法来实现运行效率：

import numpy as np
X=np.array([[1,0,-1]])
np.transpose(X)
W=np.array([[-5],[0],[0]])
t=1
lr=1
for i in range(100):
    y=np.sign(np.dot(X,W))
    print("y:",y)
    if y!=t:
        W=W+lr*(t-y)*X.T
        print(W)
    else:
        break

y: [[-1]]
[[-3]
 [ 0]
 [-2]]
y: [[-1]]
[[-1]
 [ 0]
 [-4]]
y: [[1]]

运行成功

4.学习率

（1）学习率η的取值范围一般为0～1；

（2）学习率太大，容易造成权值调整不稳定；

（3）学习率太小，模型参数调整太慢，迭代次数太多。

5.模型的收敛条件

（1）loss小于某个预先设定的较小的值；

（2）两次迭代之间权值的变化已经很小了；

（3）设定最大迭代次数，当迭代次数超过最大迭代次数时停止。

6.模型的超参数和参数的区别

 (1)前面提到的权值和偏置值则是参数

 (2)学习率和迭代次数是人为设置的超参数

1.4 单层感知器解决分类问题

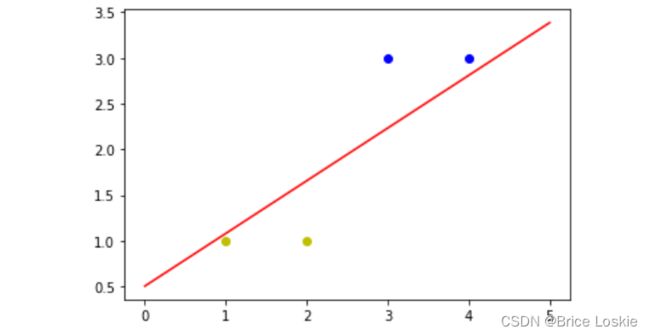
假设我们有四个二维的数据（3，3），（4，3），（1，1），（2，1）。

（3，3）和（4，3）这两个数据的标签为1，（1，1）和（2，1）这两个数据的标签为-1

我们通过此数据来构建单层感知机分类器。

我们通过单层感知器的第二种表达式来进行数据的修改

数据修改成为1，3，3），（1，4，3），（1，1，1），（1，2，1）

对应标签还是（1,1,-1,-1）

初始化权值w1，w2，w3：取0～1的随机数

学习率：取0.1

激活函数：np.sign

我们构建感知机的代码如下：

1.导包

import numpy as np
import matplotlib.pyplot as plt

2.生成数据

X=np.array([[1,3,3],[1,4,3],[1,1,1],[1,2,1]])
T=np.array([[1],[1],[-1],[-1]])
W = np.random.random([3,1])
lr =0.1
Y=0

X为样本点

T为真实的目标值

W为初始化的参数值取0-1的随机值

学习率为lr=0.1

Y为神经网络的初始化输出Y=0

for i in range(100):
    Y=np.sign(np.dot(X,W))

先得到Y的预测值

for i in range(50):
    Y=np.sign(np.dot(X,W))
    print("Y:",Y)
    E = T - Y

 对参数进行跟新

    delta_W = lr*(np.dot(X.T,E))/X.shape[0]
    W=W+delta_W

    if(Y==T).all():
        print("Finished")
        break

 当预测值全部等于真实值的时候停止跟新，函数收敛

x_1=[3,4]
y_1=[3,3]
x_2=[1,2]
y_2=[1,1]
k = -W[1]/W[2]
d = -W[0]/W[2]
xdata=(0,5)
plt.plot(xdata,xdata*k+d,'r')
plt.scatter(x_1,y_1,c='b')
plt.scatter(x_2,y_2,c='y')
plt.show()

 得到结果如图所示