MMORPG大型游戏设计与开发（服务器 游戏场景 地图和区域）

地图的数据以及区域的信息是场景的重要组成部分，这些数据同时存在客户端和服务器，而且都是由编辑器生成的。那么保存的文件数据结构是怎样的？一张3D的场景地图又是怎样处理这些数据的？同时告诉大家这里同样只是讲的理论与设计，理论和设计往往都很空洞，但是却很灵活，需要靠每个人怎么运用。

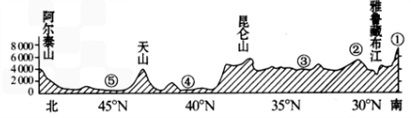
一些图片

  

区域和格子

  从上面的截图可以看出游戏场景其实是由格子来区分的，不管是矩形的格子还是其他形状的格子也好，一张地图不可能只有一个点（即多点组成一张地图）。在3D场景中似乎格子的位置总伴随着高度信息，所以让人感觉有些迷茫，其实我们可以将这些格子平铺成一张图。

  如上面的最后一张图，是地形的剖面图，不过是横切面，如果我们看一下纵切面的话，就可以将3D的地图进行2D的转换。其实地图还是由一张平面图组成，只是多了Y轴的数据，也就是我们常说的地表高度。

地图数据

  由指定格式的数据组成，在服务器和客户端的主要作用是用来寻路（点击地图走路，以及自动寻路）。

地图区域

  一个场景一般情况下会有区域的划分，因为这些区域会有自己特殊的事件，如一个玩家加入该区域会产生某个事件，就像我们玩游戏的时候忽然触发了剧情一样，这都是区域的事件。

数据结构

  有了指定的数据结构后，文件才能被正常的读取，而地图的数据一般是由编辑器生成，所以也必须规定文件的数据结构。

  1、地图

    1. 文件数据

      武侠世界/天龙八部的场景地图数据格式为：[文件头][单元数据][单元数据]…… 单元数据的数量为地图横长* 地图纵长。

       code.

typedef struct map_header_struct {
  int16_t flag; //文件标记，用来区分是不是地图数据文件
  int32_t xsize; //X方向大小 横长
  int32_t zsize; //Y方向大小 纵长 
} map_header_t; //文件头信息

typedef struct map_unit_struct {
  int16_t flag; //标识信息
                //00000000|00000000
                //               ||_ WalkDisable  -是否禁止地面上行走的OBJ穿越  [0 可穿越  1不可穿越]
                //               |__ FlyDisable   -是否禁止空中飞行的OBJ穿越    [0 可穿越  1不可穿越]
  int8_t height; //高度
  int8_t reserved; //预留字段
} map_unit_t; //单元数据信息

    2. 对象数据

     整个对象也就是整张地图的数据，在武侠世界/天龙八部中采用的是左手坐标系，而在服务器其实用不着空间的坐标也就是Y轴的数据，将地图切割后就是一张平面的图，这张平面的图一般都是矩形。

     X坐标 左为0、右为最大（也可以说是地图横长）

     Y坐标 上为0、下为最大（也可以说是地图纵长）

     code.

/* 完整的地图示意图 */
//                (0, z)   (x, z)
//                ___________
//   y  z         |         |
//   | /          |         |
//   |/           |         |
//   +-------x    |_________|
//   
//               (0, 0)    (x, 0)

  2、区域

    地图划分成一个个格子，而组成区域的也是格子，以下为一个区域的基本数据。

    1. RECT（矩形格子）

      left 左、top 高度、right 右、bottom 底部。

    2. 区域ID

    3. 脚本ID

算法（选择排序）

  1、简单选择排序

    简单选择排序基本思想是将最小的数据移动到第一个位置并交换数据，比如有N个元素，一次将最小的元素移动到第一个位置并交换数据，那么剩下的就只剩下N-1个数据，将剩下的N-1的序列的数据最小的数据移动到该剩下序列的第一个位置，这样移动N次之后，序列便成了有序的序列。

    code.

#include <stdio.h>
#include <stdint.h>
#include <inttypes.h>

/**
 * 简单选择排序基本思想是将最小的数据移动到第一个位置并交换数据，比如有N个元素，
 * 第一次将最小的元素移动到第一个位置并交换数据，那么剩下的就只剩下N-1个数据
 * 再将剩下的N-1的序列的数据最小的数据移动到该剩下序列的第一个位置，这样移动N次
 * 之后，序列便成了有序的序列。
 */

//简单选择排序
void selectsort(int32_t array[], int32_t length);
//数组打印
void displayarray(int32_t array[], int32_t length);

int32_t main(int32_t argc, char *argv[]) {
  int32_t array[] = {32, 1, 6, 9, 37, 88, 47, 35, 99};
  int32_t length = sizeof(array) / sizeof(array[0]);
  selectsort(array, length);
  printf("sort result: ");
  displayarray(array, length);
  return 0;
}

void selectsort(int32_t array[], int32_t length) {
  int32_t i, j, k;
  int32_t temp;
  //将第i个元素与第i+1...length个元素比较，将最小的元素放在第i个位置
  for (i = 0; i < length - 1; ++i) {
    j = i;
    for (k = i + 1; k < length; ++k) { //最小元素的序号为j
      if (array[k] < array[j])
        j = k;
    }
    if (j != i) { //如果序号i不等于j，则需要加序号i和序号j的元素交换
      temp = array[i];
      array[i] = array[j];
      array[j] = temp;
    }
    printf("the %d times sort result: ", i + 1);
    displayarray(array, length);
  }
}

void displayarray(int32_t array[], int32_t length) {
  int32_t i;
  for (i = 0; i < length; ++i)
    printf("%4d", array[i]);
  printf("\n");
}

    result.

  2、堆排序

    堆排序算法实现比较复杂，它主要适用于大规模的数据排序，比如在10万个数据元素中找出前10个最小或是最大的元素，使用该算法效率最高。

    code.

#include <stdio.h>
#include <stdint.h>
#include <inttypes.h>

/**
 * 堆排序算法实现比较复杂，它主要适用于大规模的数据排序，比如在10万个数据元素
 * 中找出前10个最小或是最大的元素，使用该算法效率最高。
 */

//数组打印
void displayarray(int32_t array[], int32_t length);
//调整array[pos1...pos2]，使其成为一个大顶堆
void adjustheap(int32_t array[], int32_t pos1, int32_t pos2);
//创建大顶堆
void createheap(int32_t array[], int32_t length);
//利用堆排序算法对数组进行排序
void heapsort(int32_t array[], int32_t length);

int32_t main(int32_t argc, char *argv[]) {
  int32_t array[] = {32, 1, 6, 9, 37, 88, 47, 35, 99};
  int32_t length = sizeof(array) / sizeof(array[0]);
  printf("before sort: ");
  displayarray(array, length);
  heapsort(array, length);
  printf("after sort: ");
  displayarray(array, length);
  return 0;
}

void displayarray(int32_t array[], int32_t length) {
  int32_t i;
  for (i = 0; i < length; ++i)
    printf("%4d", array[i]);
  printf("\n");
}

void adjustheap(int32_t array[], int32_t pos1, int32_t pos2) {
  int32_t i;
  int32_t temp;
  temp = array[pos1]; //临时存放根节点
  for (i = 2 * pos1 + 1; i <= pos2; i *= 2 + 1) {
    if (i < pos2 && array[i] < array[i + 1]) //从关键字较大的子节点向下筛选
      ++i; //i为关键字较大的节点的下标
    if (temp > array[i]) break; //如果子节点的值小于根节点的值，则不进行交换
    array[pos1] = array[i];
    pos1 = i;
  }
  array[pos1] = temp; //将根节点插入到正确的位置
}

void createheap(int32_t array[], int32_t length) {
  int32_t i;
  for (i = length / 2 - 1; i >= 0; --i) //从序号length / 2 - 1开始建立大顶堆
    adjustheap(array, i, length - 1);
}

void heapsort(int32_t array[], int32_t length) {
  int32_t i;
  int32_t temp;
  createheap(array, length); //创建堆
  for (i = length - 1; i > 0; --i) { //将堆顶元素与最后一个元素交换，重新调整堆
    temp = array[0];
    array[0] = array[i];
    array[i] = temp;
    printf("the %d sort times: ", length - i);
    displayarray(array, length);
    adjustheap(array, 0, i - 1); //将array[0...i-1]调整为大顶堆
  }
}

    result.