机器学习之KNN算法原理

1 KNN算法简介

KNN(K近邻) 作为最基本一种机器学习算法，其使用连续值特征。算法思想的有效性使得它能够用于分类，回归，降维，矩阵分解，聚类，异常值检测等等，其中既有监督，也有无监督算法。而我们将只从分类算法展开，理解 KNN 的具体实现过程即可。

---

2 算法思想

KNN 的算法思想是给定预测数据，在固定数据集空间中找到与它最相邻(相似)的K个数据，最后使用多数表决法决定预测数据的类别。作为一个懒惰学习算法(Lazy learning)，其本身并没有损失函数与相关参数。

---

3 多种距离度量公式

虽然 KNN 可选择距离公式有很多，但是只需知道几种比较重要的即可。
在展示以下距离公式前，假定数据集的特征序列为{$x_1,x_2...x_n$}，预测(Prediction)数据为 $P$，相对比的单个数据为 $X$。

① 欧氏距离(Euclidean distance)

欧式距离应该是最简单，最常用的距离公式了，公式为
$$D(P,X)=\sqrt{{(p_1-x_1)}^2+{(p_2-x_2)}^2+...+{(p_n-x_n)}^2}=\sqrt{\sum _{i=1}^n(p_i-x_i{)}^2}$$

② 曼哈顿距离(Manhattan distance)

曼哈顿距离使用的则是绝对值距离，公式为
$$D(P,X)=|p_1-x_1|+|p_2-x_2|+...+|p_n-x_n|=\sum _{i=1}^n|p_i-x_i|$$

推理曼哈顿距离与欧式距离的区别会发现，如果两个点之间的欧氏距离如果相同，那么越靠近坐标轴的点，其曼哈顿距离越小。

③ 闵式距离(Minkowski distance)

闵式距离又称闵可夫斯基距离，它可以看作是差值向量的 $\alpha -Norm$ ( 先前介绍的曼哈顿距离与欧氏距离则分别是特殊的 $1-Norm$ 与 $2-Norm$ )，其中 $\alpha$ 为大于 $0$ 的常数，公式有
$$D(P,X)=\sqrt[\alpha ]{\sum _{i=1}^n{|p_i-x_i|}^{\alpha }}$$

④ 标准化欧氏距离(Standardized Ed)

标准化欧式距离是针对传统距离公式无法解决各个特征维度之间的分布不同。就像由于特征之间数级尺度不同，进行梯度下降法之前要先对数据进行归一化。如果我们提前进行标准化，也能解决这个问题，而标准欧氏距离则可以通过更改内部公式，加入方差的倒数项 $s_i$ 来解决。公式为
$$D(P,X)=\sqrt{\sum _{i=1}^n(\frac{p_i-x_i}{s_i}{)}^2}$$

⑤ 余弦距离(Cosine distance)

这里为了方便余弦距离公式的书写，其中 $P$ 代表的是单个预测数据的行向量，$X^i$ 代表的是数据集中第 $i$ 个数据的列向量。公式有
$$Cos(P,X^i)=\frac{P{X}^i}{{||P||}_2{||X^i||}_2}$$

⑥ 切比雪夫距离(Chebyshev distance)

切比雪夫距离是寻求所有特征中差值绝对值最大的那一个，公式为
$$D(P,X)=\max |p_i-x_i|i\in \{x_1,x_2...x_n\}$$

---

4 三种算法实现

① Brute(蛮力)

Brute指的就是穷尽搜索，对于KNN算法，对每一个预测实力都会把所有的数据计算一遍，然后排序，取得自己想要的那 $K$ 个最相近点，最后投票表决。对于单个实例，算法预测的时间复杂度为 $O(n)$。

② KD-Tree

KD树(K-Dimension-Tree)作为一个经典的树模型，通过建立类似二叉排序树减少算法搜索时间。
此时算法可分为两个步骤，第一是建立树模型，第二是搜索邻近点进行预测。假设数据有n个特征。

第一步建立树模型，分别计算所有特征的方差，然后找到其中最大的方差所对应的特征作为分割特征，分割依据是其选择中位节点作为根节点，小于该中位节点的数据分入左子树，大于该中位节点的分入右子树。最后递归生成，直到某个节点无法再分出两个子节点为止。

下面以数据 $[(7,2),(5,4),(9,6),(4,7),(8,1),(2,3)]$为例构建KD树

1. 计算两个特征的方差，从左到右结果依次为6.97，5.37，因此选择第一个特征作为分割特征
2. 随后找到中位节点，为中位数6.5四舍五入后所靠近的（7，2）,接下来切割数据，选择(7,2)作为根节点，小于等于它的分入左子树(可能存在(7,3),因此是小于等于)，大于它的分入右子树
3. 递归生成树，知道某个节点无法分出两个子节点为止
   展示一下 wiki百科 的kd树结果图为
   
   

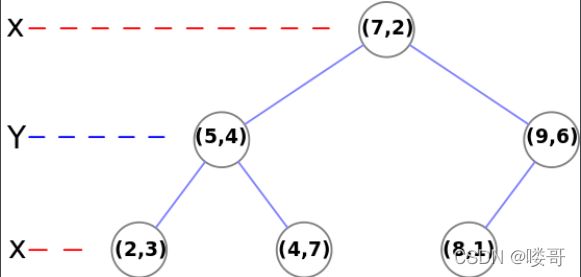
第二步则是搜索K邻近点。有幸在著名论坛 stackoverflow 中找到了一篇详细解释 KD-tree 的文章，重点在 page 3，附上文章链接book introduce

它的思想是自上而下在递归寻找到预测数据的位置的同时更新最近邻点(小于等于走左边，大于走右边)，当达到叶节点时，算作更新结束。此时得到最近邻点，以它与预测点的距离D做超球体，如果超球体相交了分类的超平面，那么就更新当前最近邻点在其另一个子节点的位置；如果超球体不相交，那么就不跟新找到的最近邻点。最后标记该最近邻点，在寻找次最近邻点时忽略它的存在。

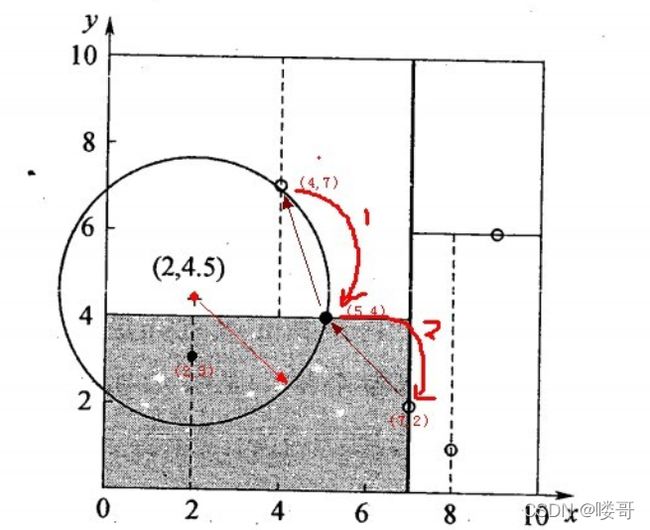
我们寻找预测点(2,4.5)的最近邻点为例

1. 从(7,2)开始，2<7：找到(5,4)。4.5>4：找到(4,7)；此时已经抵达了叶节点，停止寻找。搜索路径为 <(7,2),(5,4),(4,7)>，在此路径中寻找到的最近点为(5,4)
2. 根据(2,4.5)与(5,4)的欧氏距离做超球体，发现与其他分类超平面相交，则说明(5,4)的另一侧存在最近邻点，更新其为(2,3)
   

③ Ball-Tree

当特征数量十分多时，KD-Tree会出现沿着笛卡尔搜索数据效率低下的问题。为此出现了基于KD-Tree改进的Ball-Tree，但是其在构建球树时花费的时间会远大于KD-Tree。总的来说，Ball-Tree在高维度特征下预测时比KD-Tree更有效，但构建时间也更长。

第一步，球树的构建流程

1. 首先创造一个包含所有样本的最小超球体
2. 从超球体中选择一个离球心最远的点，然后选择另外一个点，它离第一个点最远
3. 将剩下来的所有点分配到离那两个点(聚类中心)上，离谁近就分给谁，最后已经分配好数据分别根据两个聚类中心分别构建两个最小子球体
4. 对子球体重复以上2，3步
5. 终止条件：某子球体中只剩下一或两个点时，该子球体停止划分

给出一张已划分球树的图加强理解

第二步，搜索K近邻点
博主能力有限(实际上是不想在这个上花费不必要的时间 T_T)，由于目前尚未查询到详细解释ball-tree neighbor search的资料，相关博客看的也是一知半解，较为模糊。如果日后有机会再次接触ball-tree，回来补全原理。