【吴恩达深度学习编程作业】4.1卷积神经网络——搭建卷积神经网络模型以及应用

参考文章：搭建卷积神经网络以及应用

神经网络的底层搭建

实现一个拥有卷积层CONV和池化层POOL的网络，包含前向和反向传播

• CONV模块包括：
  使用0扩充边界：没有缩小高度和宽度；保留边界的更多信息
  卷积窗口
  前向卷积
  反向卷积
• POOL模块包括：
  前向池化
  创建掩码
  值分配
  反向池化

main.py

import numpy as np
import matplotlib.pyplot as plt

plt.rcParams['figure.figsize'] = (5.0, 4.0)
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'

np.random.seed(1)


# 1.1边界填充
# constant连续一样的值填充，有constant_value=(x,y)时前面用x填充，后面用y填充，缺省参数是为constant_values=(0,0)
def zero_pad(X, pad):
    """
        把数据集X的图像边界全部用0来扩充pad个宽度和高度
    :param X:   -图像数据集，维度为（样本数，图像高度，图像宽度，图像通道数）
    :param pad: -整数，每个图像在垂直和水平维度上的填充量
    :return: X_paded    -扩充后的图像数据集，维度为（样本数，图像高度+2*pad，图像宽度+2*pad， 图像通道数）
    """

    X_paded = np.pad(X, ((0, 0),         # 样本数，不填充
                         (pad, pad),     # 图像高度，在上面填充x个，在下面填充y个（x,y）
                         (pad, pad),     # 图像宽度，在左边填充x个，在右边填充y个（x,y）
                         (0, 0)),        # 通道数，不填充
                        'constant', constant_values=0)  # 连续一样的值填充

    return X_paded

print("====================测试zero_pad===================")
np.random.seed(1)
x = np.random.randn(4, 3, 3, 2)
print(x)
x_paded = zero_pad(x, 2)
print("x.shape = ", x.shape)
print("x_paded.shape = ", x_paded.shape)
print("x[1, 1] = ", x[1, 1])
print("x_paded[1, 1] = ", x_paded[1, 1])
"""
    运行结果：
        x.shape =  (4, 3, 3, 2)
        x_paded.shape =  (4, 7, 7, 2)
        x[1, 1] =  [[ 0.90085595 -0.68372786]
                     [-0.12289023 -0.93576943]
                     [-0.26788808  0.53035547]]
        x_paded[1, 1] =  [[0. 0.]
                         [0. 0.]
                         [0. 0.]
                         [0. 0.]
                         [0. 0.]
                         [0. 0.]
                         [0. 0.]]
"""

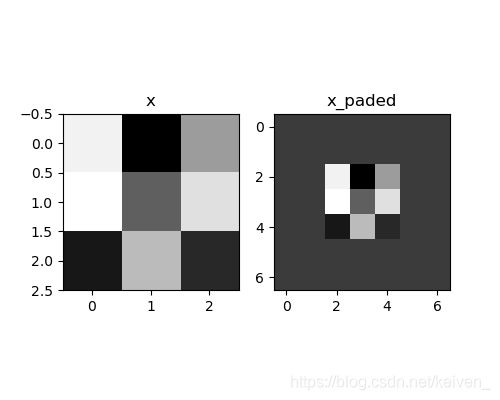
# 绘制图
fig, axarr = plt.subplots(1, 2)  # 一行两列
axarr[0].set_title('x')
axarr[0].imshow(x[0, :, :, 0])
axarr[1].set_title('x_paded')
axarr[1].imshow(x_paded[0, :, :, 0])
plt.show()


# 1.2单步卷积
def conv_single_step(a_slice_prev, W, b):
    """
    在前一层的激活输出一个片段上应用一个由参数W定义的过滤器
    这里切片大小和过滤器大小相同
    :param a_slice_prev:    -输入数据的一个片段，维度为（过滤器大小，过滤器大小，上一层通道数）
    :param W:   -权重参数，包含在一个矩阵中，维度为（过滤器大小，过滤器）
    :param b:   -偏置参数，包含在一个矩阵中，维度为（1,1,1）
    :return:Z   -在输入数据的片X上卷积滑动窗口（w,b）的结果
    """
    s = np.multiply(a_slice_prev, W) + b
    Z = np.sum(s)
    return Z

print("=================测试conv_single_step=====================")
np.random.seed(1)
# 切片大小和过滤器大小相同
a_slice_prev = np.random.randn(4, 4, 3)
W = np.random.randn(4, 4, 3)
b = np.random.randn(1, 1, 1)
Z = conv_single_step(a_slice_prev, W, b)
print("Z = " + str(Z))      # Z = -23.16021220252078


# 1.3卷积神经网络-前向传播
def conv_forward(A_prev, W, b, hparameters):
    """
    实现卷积函数的前向传播
    :param A_prev:  -上一层的激活输出矩阵，维度为(m, n_H_prev, n_W_prev, n_c_prev),(样本数量，上一层图像的高度，上一层图像的宽度，上一层过滤器数量)
    :param W:   -权重矩阵，维度为(f, f, n_c_prev, n_c),(过滤器大小，过滤器大小，上一层的过滤器数量，这一层的过滤器数量)
    :param b:   -偏置矩阵，维度为(1, 1, 1, n_c),(1, 1, 1, 这一层的过滤器数量)
    :param hparameters:     -包含了"stride"与"pad"的超参数字典
    :return: Z  -卷积输出，维度为(m. n_H, n_W, n_c),(样本数，图像的高度，图像的宽度，过滤器的数量)
             cache  -缓存了一些反向传播函数conv_backward()需要的一些数据
    """

    # 获取来自上一层数据的基本信息
    (m, n_H_prev, n_W_prev, n_c_prev) = A_prev.shape

    # 获取权重矩阵的基本信息
    (f, f, n_c_prev, n_c) = W.shape

    # 获取超参数hparameters的值
    stride = hparameters["stride"]
    pad = hparameters["pad"]

    # 计算卷积后的图像的宽度高度，使用int()进行地板除
    n_H = int((n_H_prev - f + 2 * pad) / stride) + 1
    n_W = int((n_W_prev - f + 2 * pad) / stride) + 1

    # 使用0初始化卷积输出Z
    Z = np.zeros((m, n_H, n_W, n_c))

    # 通过A_prev创建填充过的A_prev_pad
    A_prev_pad = zero_pad(A_prev, pad)

    for i in range(m):                  # 遍历样本
        a_prev_pad = A_prev_pad[i]      # 选择第i个样本的扩充后的激活矩阵
        for h in range(n_H):            # 在输出的垂直轴上循环
            for w in range(n_W):        # 在输出的水平轴上循环
                for c in range(n_c):    # 循环遍历输出的通道
                    # 定位当前的切片位置
                    vert_start = h * stride         # 竖向开始的位置
                    vert_end = vert_start + f       # 竖向结束的位置
                    horiz_start = w * stride        # 横向开始的位置
                    horiz_end = horiz_start + f     # 横向结束的位置
                    # 切片位置定位好了把它取出，“穿透”取出
                    a_slice_prev = a_prev_pad[vert_start: vert_end, horiz_start: horiz_end, :]
                    # 执行单步卷积
                    Z[i, h, w, c] = conv_single_step(a_slice_prev, W[:, :, :, c], b[0, 0, 0, c])

    # 数据处理完毕，验证数据格式是否正确
    assert (Z.shape == (m, n_H, n_W, n_c))

    # 存储一些缓存值，以便于反向传播使用
    cache = (A_prev, W, b, hparameters)

    return (Z, cache)


print("====================测试conv_forward=====================")
np.random.seed(1)

A_prev = np.random.randn(10, 4, 4, 3)
W = np.random.randn(2, 2, 3, 8)
b = np.random.randn(1, 1, 1, 8)

hparameters = {"pad": 2, "stride": 1}

Z, cache_conv = conv_forward(A_prev, W, b, hparameters)

print("np.mean(Z) = ", np.mean(Z))      # np.mean(Z) =  0.15585932488906465
# cache_conv是一个五维数组，数组的第一个索引分别包括A_prev，W，b，hparameters
print("cache_conv[0][1][2][3] = ", cache_conv[0][1][2][3])  # cache_conv[0][1][2][3] =  [-0.20075807  0.18656139  0.41005165]
print(cache_conv[3])    # {'pad': 2, 'stride': 1}
"""
    # 卷积层应该包含一个激活函数
    # 获取输出
    Z[i, h, w, c] = ...
    # 计算激活
    A[i, h, w, c] = activation(Z[i, h, w, c])
"""


# 1.4池化层的前向传播
def pool_forward(A_prev, hparameters, mode="max"):
    """
    实现池化层的前向传播
    :param A_prev:  -输入数据，维度为(m, n_H_prev, n_W_prev, n_C_prev)
    :param hparameters:     -包含了"f"和"stride"的超参数字典
    :param mode:            -模式选择【"max" | "average"】
    :return: A              -池化层的输出，维度为(m, n_H, n_W, n_C)
             cache          -存储了一些反向传播用到的值，包含输入和超参数的字典
    """

    # 获取输入数据的基本信息
    (m, n_H_prev, n_W_prev, n_c_prev) = A_prev.shape

    # 获取超参数的信息
    f = hparameters["f"]
    stride = hparameters["stride"]

    # 计算输出维度
    n_H = int((n_H_prev - f) / stride) + 1
    n_W = int((n_W_prev - f) / stride) + 1
    n_c = n_c_prev

    # 初始化输出矩阵
    A = np.zeros((m, n_H, n_W, n_c))

    for i in range(m):                  # 遍历样本
        for h in range(n_H):            # 在输出的垂直轴上循环
            for w in range(n_W):        # 在输出的水平轴上循环
                for c in range(n_c):    # 循环遍历输出的通道
                    # 定位当前的切片位置
                    vert_start = h * stride         # 竖向开始的位置
                    vert_end = vert_start + f       # 竖向结束的位置
                    horiz_start = w * stride        # 横向开始的位置
                    horiz_end = horiz_start + f     # 横向结束的位置
                    # 定位完毕，开始切割
                    a_slice_prev = A_prev[i, vert_start: vert_end, horiz_start: horiz_end, c]

                    # 对切片进行池化操作
                    if mode == "max":
                        A[i, h, w, c] = np.max(a_slice_prev)
                    elif mode == "average":
                        A[i, h, w, c] = np.mean(a_slice_prev)

    # 数据处理完毕，验证数据格式
    assert (A.shape == (m, n_H, n_W, n_c))

    # 校验完毕，存储用于反向传播的值
    cache = (A_prev, hparameters)

    return A, cache


print("=========================测试pool_forward====================")
np.random.seed(1)
A_prev = np.random.randn(2, 4, 4, 3)
hparameters = {"f": 4, "stride": 1}

A, cache = pool_forward(A_prev, hparameters, mode="max")
print("mode = max")
print("A = ", A)

A, cache = pool_forward(A_prev, hparameters, mode="average")
print("mode = average")
print("A = ", A)

"""
    运行结果：
        mode = max
        A =  [[[[1.74481176 1.6924546  2.10025514]]]
        
        
         [[[1.19891788 1.51981682 2.18557541]]]]
        mode = average
        A =  [[[[-0.09498456  0.11180064 -0.14263511]]]
        
        
         [[[-0.09525108  0.28325018  0.33035185]]]]
"""

# 1.5卷积神经网络中的反向传播：一般只需实现前向传播，反向传播由框架完成

运行结果

神经网络的应用

main.py

import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow.python.framework import ops
import Deep_Learning.test4_1.cnn_utils


# 加载数据集，数据集同test2_3
X_train_orig, Y_train_orig, X_test_orig, Y_test_orig, classes = Deep_Learning.test4_1.cnn_utils.load_dataset()
index = 6
plt.imshow(X_train_orig[index])
plt.show()
print("Y = " + str(np.squeeze(Y_train_orig[:, index])))     # Y = 2


# 对数据集进行扁平化，然后除以255归一化数据，还需要把每个标签转化为独热向量
# 归一化数据
X_train = X_train_orig / 255
X_test = X_test_orig / 255

# 转换为独热矩阵
Y_train = Deep_Learning.test4_1.cnn_utils.convert_to_one_hot(Y_train_orig, 6).T
Y_test = Deep_Learning.test4_1.cnn_utils.convert_to_one_hot(Y_test_orig, 6).T

print("训练集样本数 = " + str(X_train.shape[0]))                  # 训练集样本数 = 1080
print("测试集样本数 = " + str(X_test.shape[0]))                   # 测试集样本数 = 120
print("X_train.shape:" + str(X_train.shape))                    # X_train.shape:(1080, 64, 64, 3)
print("Y_train.shape:" + str(Y_train.shape))                    # Y_train.shape:(1080, 6)
print("X_test.shape:" + str(X_test.shape))                      # X_test.shape:(120, 64, 64, 3)
print("Y_test.shape:" + str(Y_test.shape))                      # Y_test.shape:(120, 6)
conv_layers = {}


# 2.1创建placeholders
def create_placeholders(n_H0, n_W0, n_c0, n_y):
    """
    为session创建占位符
    :param n_H0:    -实数，输入图像的高度
    :param n_W0:    -实数，输入图像的宽度
    :param n_c0:    -实数，输入的通道数
    :param n_y:     -实数，分类数
    :return: X      -输入数据的占位符，维度为[None,n_H0,n_W0,n_C0]，类型为"float"
             Y      -输入数据的标签的占位符，维度为[None,n_y],类型为"float"
    """
    X = tf.placeholder(tf.float32, [None, n_H0, n_W0, n_c0])
    Y = tf.placeholder(tf.float32, [None, n_y])

    return X, Y

print("===================测试create_placeholders===============")
X, Y = create_placeholders(64, 64, 3, 6)
print("X = " + str(X))
print("Y = " + str(Y))
"""
    运行结果：
        X = Tensor("Placeholder:0", shape=(?, 64, 64, 3), dtype=float32)
        Y = Tensor("Placeholder_1:0", shape=(?, 6), dtype=float32)
"""


# 2.2初始化参数
def initialize_parameters():
    """
    初始化权重矩阵，这里把权重矩阵硬编码：
        W1:[4, 4, 3, 8]
        W2:[2, 2, 8, 16]
    :return: 包含了tensor类型的W1和W2字典
    """
    tf.set_random_seed(1)

    W1 = tf.get_variable("W1", [4, 4, 3, 8], initializer=tf.contrib.layers.xavier_initializer(seed=0))
    W2 = tf.get_variable("W2", [2, 2, 8, 16], initializer=tf.contrib.layers.xavier_initializer(seed=0))

    parameters = {"W1": W1,
                  "W2": W2}

    return parameters


print("======================测试initialize_parameters==================")
tf.reset_default_graph()
with tf.Session() as sess_test:
    parameters = initialize_parameters()
    init = tf.global_variables_initializer()
    sess_test.run(init)
    print("W1 = " + str(parameters["W1"].eval()[1, 1, 1]))
    print("W2 = " + str(parameters["W2"].eval()[1, 1, 1]))
    sess_test.close()
"""
    运行结果：
        W1 = [ 0.00131723  0.1417614  -0.04434952  0.09197326  0.14984085 -0.03514394 -0.06847463  0.05245192]
        W2 = [-0.08566415  0.17750949  0.11974221  0.16773748 -0.0830943  -0.08058 -0.00577033 -0.14643836  
               0.24162132 -0.05857408 -0.19055021  0.1345228 -0.22779644 -0.1601823  -0.16117483 -0.10286498]
"""


# 2.3前向传播
def forward_propagation(X, parameters):
    """
    实现前向传播
        CONV2D -> RELU -> MAXPOOL -> CONV2D -> RELU -> MAXPOOL -> FLATTEN -> FULLYCONNECTED
    :param X:   -输入数据的placeholder，维度为(输入节点数量，样本数量)
    :param parameters:  -包含了"W1"和"W2"的python字典
    :return:Z3  -最后一个LINEAR节点的输出
    """
    W1 = parameters["W1"]
    W2 = parameters["W2"]

    # Conv2d: 步伐1，填充方式"SAME"
    Z1 = tf.nn.conv2d(X, W1, strides=[1, 1, 1, 1], padding="SAME")
    # Relu:
    A1 = tf.nn.relu(Z1)
    # Max pool:过滤器大小8×8，步伐8×8，填充方式"SAME"
    P1 = tf.nn.max_pool2d(A1, ksize=[1, 8, 8, 1], strides=[1, 8, 8, 1], padding="SAME")

    # Conv2d: 步伐1，填充方式"SAME"
    Z2 = tf.nn.conv2d(P1, W2, strides=[1, 1, 1, 1], padding="SAME")
    # Relu:
    A2 = tf.nn.relu(Z2)
    # Max pool:过滤器大小4×4，步伐4×4，填充方式"SAME"
    P2 = tf.nn.max_pool2d(A2, ksize=[1, 4, 4, 1], strides=[1, 4, 4, 1], padding="SAME")

    # 一维化上一层的输出
    P = tf.contrib.layers.flatten(P2)

    # 全连接层（FC）：使用没有非线性激活函数的全连接层
    Z3 = tf.contrib.layers.fully_connected(P, 6, activation_fn=None)

    return Z3

print("======================测试forward_propagation======================")
tf.reset_default_graph()
np.random.seed(1)

with tf.Session() as sess_test:
    X, Y = create_placeholders(64, 64, 3, 6)
    parameters = initialize_parameters()
    Z3 = forward_propagation(X, parameters)

    init = tf.global_variables_initializer()
    sess_test.run(init)

    a = sess_test.run(Z3, {X: np.random.randn(2, 64, 64, 3), Y: np.random.randn(2, 6)})
    print("Z3 = " + str(a))

    sess_test.close()
"""
    运行结果：
        Z3 = [[ 1.4416982  -0.24909668  5.4504995  -0.2618962  -0.20669872  1.3654671 ]
        [ 1.4070847  -0.02573182  5.08928    -0.4866991  -0.4094069   1.2624853 ]]
"""

# 2.4计算成本
def compute_cost(Z3, Y):
    """
    计算成本
    :param Z3:  -正向传播最后一个LINEAR节点的输出，维度为(6,样本数)
    :param Y:   -标签向量的placeholder,和Z3的维度相同
    :return: cost   -计算后的成本
    """

    cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=Z3, labels=Y))

    return cost

print("===================测试compute_cost==================")
tf.reset_default_graph()

with tf.Session() as sess_test:
    np.random.seed(1)
    X, Y = create_placeholders(64, 64, 3, 6)
    parameters = initialize_parameters()
    Z3 = forward_propagation(X, parameters)
    cost = compute_cost(Z3, Y)

    init = tf.global_variables_initializer()
    sess_test.run(init)
    a = sess_test.run(cost, {X: np.random.randn(4, 64, 64, 3), Y: np.random.randn(4, 6)})
    print("cost = " + str(a))

    sess_test.close()
"""
    运行结果：
        cost = 4.6648703
"""

# 2.5构建模型
"""
    创建占位符；初始化参数；前向传播；计算成本；反向传播；创建优化器
"""
def model(X_train, Y_train, X_test, Y_test, learning_rate=0.009,
          num_epochs=100, minibatch_size=64, print_cost=True, isPlot=True):
    """
    使用TensorFlow实现三层卷积神经网络
    :param X_train:     -训练数据，维度为(None,64,64,3)
    :param Y_train:     -训练数据对应的标签，维度为(None,n_y=6)
    :param X_test:      -测试数据，维度为(None,64,64,3)
    :param Y_test:      -训练数据对应的标签，维度为(None,n_y=6)
    :param learning_rate:   -学习率
    :param num_epochs:      -遍历整个数据集的次数
    :param minibatch_size:  -每个小批量数据块的大小
    :param print_cost:      -是否打印成本值，每遍历100次整个数据集打印一次
    :param isPlot:          -是否绘制图谱
    :return: train_accuracy -实数，训练集的准确度
             test_accuracy  -实数，测试集的准确度
             parameters     -学习后的参数
    """

    ops.reset_default_graph()   # 能够重新运行模型而不覆盖tf变量
    tf.set_random_seed(1)
    seed = 3
    (m, n_H0, n_W0, n_c0) = X_train.shape
    n_y = Y_train.shape[1]
    costs = []

    # 为当前维度创建占位符
    X, Y = create_placeholders(n_H0, n_W0, n_c0, n_y)

    # 初始化参数
    parameters = initialize_parameters()

    # 前向传播
    Z3 = forward_propagation(X, parameters)

    # 计算成本
    cost = compute_cost(Z3, Y)

    # 反向传播，框架已经实现了反向传播，我们只需要选择一个优化器就ok了
    optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate).minimize(cost)

    # 全局初始化所有变量
    init = tf.global_variables_initializer()

    # 开始运行
    with tf.Session() as sess:
        # 初始化参数
        sess.run(init)
        # 遍历数据集
        for epoch in range(num_epochs):
            minibatch_cost = 0
            num_minibatches = int(m / minibatch_size)   # 获取数据块的数量
            seed = seed + 1
            minibatches = Deep_Learning.test4_1.cnn_utils.random_mini_batches(X_train, Y_train, minibatch_size, seed)

            #对每个数据块进行处理
            for minibatch in minibatches:
                # 选择一个数据块
                (minibatch_X, minibatch_Y) = minibatch
                # 最小化这个数据块的成本
                _, temp_cost = sess.run([optimizer, cost], feed_dict={X: minibatch_X, Y: minibatch_Y})

                # 累加数据块的成本
                minibatch_cost += temp_cost / num_minibatches

            # 是否打印成本
            if print_cost:
                # 每5代打印一次
                if epoch % 5 == 0:
                    print("当前是第" + str(epoch) + "代，成本值为：" + str(minibatch_cost))

            # 记录成本
            if epoch % 1 == 0:
                costs.append(minibatch_cost)

        # 数据处理完毕，绘制成本曲线
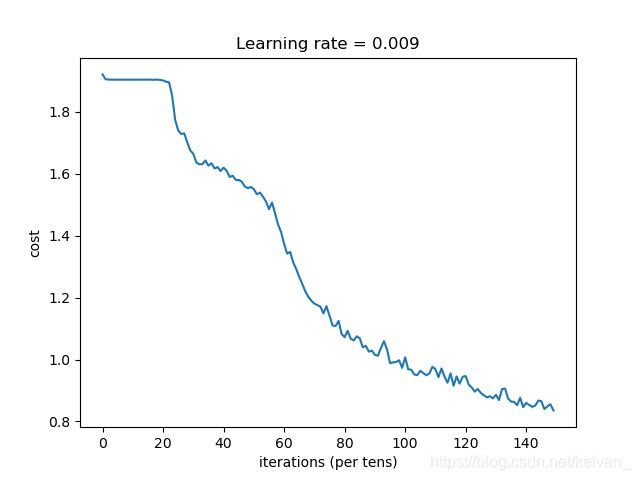
        if isPlot:
            plt.plot(np.squeeze(costs))
            plt.ylabel('cost')
            plt.xlabel('iterations (per tens)')
            plt.title("Learning rate = " + str(learning_rate))
            plt.show()

        # 开始预测数据
        ## 计算当前的预测情况
        predit_op = tf.arg_max(Z3, 1)
        corrent_prediction = tf.equal(predit_op, tf.arg_max(Y, 1))

        ## 计算准确度
        accuracy = tf.reduce_mean(tf.cast(corrent_prediction, "float"))
        print("corrent_prediction accuracy = " + str(accuracy))

        train_accuracy = accuracy.eval({X: X_train, Y: Y_train})
        test_accuracy = accuracy.eval({X: X_test, Y: Y_test})

        print("训练集的准确度：" + str(train_accuracy))
        print("测试集的准确度：" + str(test_accuracy))

        return (train_accuracy, test_accuracy, parameters)

print("=========================测试model================")
_, _, parameters = model(X_train, Y_train, X_test, Y_test, num_epochs=150)

"""
    运行结果：
        当前是第0代，成本值为：1.9213323965668678
        当前是第5代，成本值为：1.9041557759046555
        当前是第10代，成本值为：1.9043088480830193
        当前是第15代，成本值为：1.904477171599865
        当前是第20代，成本值为：1.9018685296177864
        当前是第25代，成本值为：1.7401809096336365
        当前是第30代，成本值为：1.6646495833992958
        当前是第35代，成本值为：1.626261167228222
        当前是第40代，成本值为：1.6200454384088516
        当前是第45代，成本值为：1.5801728665828705
        当前是第50代，成本值为：1.550707258284092
        当前是第55代，成本值为：1.4860153198242188
        当前是第60代，成本值为：1.3735136091709137
        当前是第65代，成本值为：1.2669073417782784
        当前是第70代，成本值为：1.1806523390114307
        当前是第75代，成本值为：1.1412195302546024
        当前是第80代，成本值为：1.0724785141646862
        当前是第85代，成本值为：1.0686000622808933
        当前是第90代，成本值为：1.0151213817298412
        当前是第95代，成本值为：0.9881901554763317
        当前是第100代，成本值为：1.0072355084121227
        当前是第105代，成本值为：0.9636502638459206
        当前是第110代，成本值为：0.9690168127417564
        当前是第115代，成本值为：0.9555537402629852
        当前是第120代，成本值为：0.946508813649416
        当前是第125代，成本值为：0.892060186713934
        当前是第130代，成本值为：0.8858786560595036
        当前是第135代，成本值为：0.8643605448305607
        当前是第140代，成本值为：0.8599357567727566
        当前是第145代，成本值为：0.8652942292392254
        corrent_prediction accuracy = Tensor("Mean_1:0", shape=(), dtype=float32)
        训练集的准确度：0.725
        测试集的准确度：0.575
"""

运行结果

cnn_utils.py

import math
import numpy as np
import h5py
import tensorflow as tf


def load_dataset():
    train_dataset = h5py.File('datasets/train_signs.h5', "r")
    train_set_x_orig = np.array(train_dataset["train_set_x"][:]) # your train set features
    train_set_y_orig = np.array(train_dataset["train_set_y"][:]) # your train set labels
    test_dataset = h5py.File('datasets/test_signs.h5', "r")
    test_set_x_orig = np.array(test_dataset["test_set_x"][:]) # your test set features
    test_set_y_orig = np.array(test_dataset["test_set_y"][:]) # your test set labels
    classes = np.array(test_dataset["list_classes"][:]) # the list of classes
    train_set_y_orig = train_set_y_orig.reshape((1, train_set_y_orig.shape[0]))
    test_set_y_orig = test_set_y_orig.reshape((1, test_set_y_orig.shape[0]))
    return train_set_x_orig, train_set_y_orig, test_set_x_orig, test_set_y_orig, classes
    
    
def random_mini_batches(X, Y, mini_batch_size = 64, seed = 0):
    """
    Creates a list of random minibatches from (X, Y)
    Arguments:
    X -- input data, of shape (input size, number of examples) (m, Hi, Wi, Ci)
    Y -- true "label" vector (containing 0 if cat, 1 if non-cat), of shape (1, number of examples) (m, n_y)
    mini_batch_size - size of the mini-batches, integer
    seed -- this is only for the purpose of grading, so that you're "random minibatches are the same as ours.
    Returns:
    mini_batches -- list of synchronous (mini_batch_X, mini_batch_Y)
    """
    m = X.shape[0]                  # number of training examples
    mini_batches = []
    np.random.seed(seed)
    # Step 1: Shuffle (X, Y)
    permutation = list(np.random.permutation(m))
    shuffled_X = X[permutation,:,:,:]
    shuffled_Y = Y[permutation,:]
    # Step 2: Partition (shuffled_X, shuffled_Y). Minus the end case.
    num_complete_minibatches = math.floor(m/mini_batch_size) # number of mini batches of size mini_batch_size in your partitionning
    for k in range(0, num_complete_minibatches):
        mini_batch_X = shuffled_X[k * mini_batch_size : k * mini_batch_size + mini_batch_size,:,:,:]
        mini_batch_Y = shuffled_Y[k * mini_batch_size : k * mini_batch_size + mini_batch_size,:]
        mini_batch = (mini_batch_X, mini_batch_Y)
        mini_batches.append(mini_batch)
    # Handling the end case (last mini-batch < mini_batch_size)
    if m % mini_batch_size != 0:
        mini_batch_X = shuffled_X[num_complete_minibatches * mini_batch_size : m,:,:,:]
        mini_batch_Y = shuffled_Y[num_complete_minibatches * mini_batch_size : m,:]
        mini_batch = (mini_batch_X, mini_batch_Y)
        mini_batches.append(mini_batch)
    return mini_batches
    
    
def convert_to_one_hot(Y, C):
    Y = np.eye(C)[Y.reshape(-1)].T
    return Y
    
    
def forward_propagation_for_predict(X, parameters):
    """
    Implements the forward propagation for the model: LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SOFTMAX
    Arguments:
    X -- input dataset placeholder, of shape (input size, number of examples)
    parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3"
                  the shapes are given in initialize_parameters
    Returns:
    Z3 -- the output of the last LINEAR unit
    """
    # Retrieve the parameters from the dictionary "parameters" 
    W1 = parameters['W1']
    b1 = parameters['b1']
    W2 = parameters['W2']
    b2 = parameters['b2']
    W3 = parameters['W3']
    b3 = parameters['b3'] 
                                                           # Numpy Equivalents:
    Z1 = tf.add(tf.matmul(W1, X), b1)                      # Z1 = np.dot(W1, X) + b1
    A1 = tf.nn.relu(Z1)                                    # A1 = relu(Z1)
    Z2 = tf.add(tf.matmul(W2, A1), b2)                     # Z2 = np.dot(W2, a1) + b2
    A2 = tf.nn.relu(Z2)                                    # A2 = relu(Z2)
    Z3 = tf.add(tf.matmul(W3, A2), b3)                     # Z3 = np.dot(W3,Z2) + b3
    return Z3


def predict(X, parameters):
    W1 = tf.convert_to_tensor(parameters["W1"])
    b1 = tf.convert_to_tensor(parameters["b1"])
    W2 = tf.convert_to_tensor(parameters["W2"])
    b2 = tf.convert_to_tensor(parameters["b2"])
    W3 = tf.convert_to_tensor(parameters["W3"])
    b3 = tf.convert_to_tensor(parameters["b3"])
    params = {"W1": W1,
              "b1": b1,
              "W2": W2,
              "b2": b2,
              "W3": W3,
              "b3": b3}
    x = tf.placeholder("float", [12288, 1])
    z3 = forward_propagation_for_predict(x, params)
    p = tf.argmax(z3)
    sess = tf.Session()
    prediction = sess.run(p, feed_dict = {x: X})
    return prediction