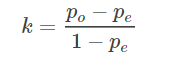分类问题的评估（二分类&多分类）

目录

 

一、准确率

二、平均准确率

三、基于相似度的评价指标

四、ROC曲线：

五、混淆矩阵（Confusion Matrix）

六、Kappa系数

七、分类报告

八、神经网络多分类问题可以用binary-crossentropy吗？

---

一、准确率

metrics.accuracy_score(y_true=y_true, y_pred=y_pred)

二、平均准确率

针对不平衡数据，对n个类，分别计算每个类别的准确率，然后求平均值。

metrics.average_precision_score(y_true=y_true, y_score=y_pred)

三、基于相似度的评价指标

3.1 log-loss

指示矩阵Y(N*K)，yi,k=1如果第i个数据属于第k类，否则yi,k=0。pi,k为预测概率。

metrics.log_loss(y_true,y_pred)

3.2 hamming_loss

metrics.hamming_loss(y_true, y_pred)

3.3 jaccard_similarity_score

metrics.jaccard_similarity_score(y_true, y_pred)

四、ROC曲线：

真正例（True Positive，TP）：真实类别为正例，预测类别为正例。
假正例（False Positive，FP）：真实类别为负例，预测类别为正例。
假负例（False Negative，FN）：真实类别为正例，预测类别为负例。
真负例（True Negative，TN）：真实类别为负例，预测类别为负例。

1、真正率（True Positive Rate , TPR）或灵敏度（sensitivity） 
TPR = TP /（TP + FN） 
正样本预测结果数 / 正样本实际数 

2、假负率（False Negative Rate , FNR） 
FNR = FN /（TP + FN） 
被预测为负的正样本结果数 / 正样本实际数 

3、假正率（False Positive Rate , FPR） 
FPR = FP /（FP + TN） 
被预测为正的负样本结果数 /负样本实际数 

4、真负率（True Negative Rate , TNR）或特指度（specificity） 
TNR = TN /（TN + FP） 
负样本预测结果数 / 负样本实际数 

目标属性的被选中的那个期望值称作是“正”（positive） 

5、准确率，又称查准率（Precision，P）：

6、召回率，又称查全率（Recall，R）：

7、F1​值：

8、F1​的一般形式：

ROC曲线是根据一系列不同的二分类方式（分界值或决定阈），以假阳性率（1-特异度）FPR为横坐标，真阳性率（灵敏度）为纵坐标绘制的曲线。传统的诊断试验评价方法有一个共同的特点：必须将试验结果分为两类，再进行统计分析。

1. 分类的类型：必须为数值型。
2. 只针对二分类问题。

ROC曲线上几个关键点的解释： 

1. ( TPR=0,FPR=0 ) 把每个实例都预测为负类的模型 
2. ( TPR=1,FPR=1 ) 把每个实例都预测为正类的模型 
3. ( TPR=1,FPR=0 ) 理想模型

一个好的分类模型应该尽可能靠近图形的左上角，而一个随机猜测模型应位于连接点（TPR=0,FPR=0）和（TPR=1,FPR=1）的主对角线上。 

AUC：ROC曲线下方的面积（AUC）提供了评价模型平均性能的另一种方法。如果模型是完美的，那么它的AUG = 1，如果模型是个简单的随机猜测模型，那么它的AUG = 0.5，如果一个模型好于另一个，则它的曲线下方面积相对较大，即值越大越好。

首先AUC值是一个概率值，介于0.1和1之间，当你随机挑选一个正样本以及负样本，当前的分类算法根据计算得到的Score值将这个正样本排在负样本前面的概率就是AUC值，AUC值越大，当前分类算法越有可能将正样本排在负样本前面，从而能够更好地分类。

常见错误：

ValueError: multiclass format is not supported
这是因为，类别数多于了两个，前面我们说过ROC只能针对二分类问题。

五、混淆矩阵（Confusion Matrix）

metrics.confusion_matrix(y_true, y_pred)

六、Kappa系数

kappa系数是用在统计学中评估一致性的一种方法，我们可以用来进行多分类模型准确度的评估，这个系数的取值范围是[-1,1]，实际应用中，一般是[0,1]，与ROC曲线中一般不会出现下凸形曲线的原理类似。
这个系数的值越高，则代表模型实现的分类准确度越高。kappa系数的计算方法可以这样来表示：

p0表示为总的分类准确度

pe表示为：

ai 代表第i类真实样本个数，

bi 代表第i类预测出来的样本个数。

def kappa(matrix):
    n = np.sum(matrix)
    sum_po = 0
    sum_pe = 0
    for i in range(len(matrix[0])):
        sum_po += matrix[i][i]
        row = np.sum(matrix[i, :])
        col = np.sum(matrix[:, i])
        sum_pe += row * col
    po = sum_po / n
    pe = sum_pe / (n * n)
    # print(po, pe)
    return (po - pe) / (1 - pe)

import numpy as np
matrix = [
    [239,21,16],
    [16,73,4]
    [6,9,280]]

matrix = np.array(matrix)
print(kappa(matrix))

七、分类报告

from sklearn.metrics import classification_report
y_true = [0, 1, 2, 2, 0]
y_pred = [0, 0, 2, 1, 0]
target_names = [‘class 0’, ‘class 1’, ‘class 2’]
print(classification_report(y_true, y_pred, target_names=target_names))

八、神经网络多分类问题可以用binary-crossentropy吗？

不能，因为binary-crossentropy > categorical_crossentropy，多分类任务应该使用categorical_crossentropy。

在多分类问题中使用binary-crossentropy，会虚假的提升的准确率。简单地说，'binary_crossentropy'不能用于多分类任务，如果使用了model.evaluate()所得到的Accuary是不对的、是没有意义的。

打个比方，我们假设多分类问题中，softmax的输出结果是 (0.1, 0.2, 0.3, 0.4)，独热编码后的结果是真值是 （0 0 0 1）。假如真值的标签是 (1, 0, 0, 0)，使用categorical_crossentropy，很明显，正确率是零；但使用binary-crossentropy，正确率是50%，因为中间的数字对了，这明显是虚假的准确率提升。

但是，model.predict()是可以用的：

y_pred = model.predict(X_test)
y_pred = y_pred.argmax(axis=1)
Y_test = Y_test.argmax(axis=1)
print('test accuracy %s' % accuracy_score(y_pred, Y_test))