并查集学习-来自leetcode
1、概念及基础
并查集是一种树形数据结构,主要用来处理一些不相交的集合合并以及查询问题。
解决图的连通性问题。
- Union – 连接两个点,
- Find – 查找所属的连同=通分量
并查集主要用来实现以下接口:
class UF{
public:
/*将p和q连接*/
public void union(int p,int q);
/*判断p和q是否连通*/
public bool connected(int p,int q);
/*返回图中有多少个连通分量*/
public int count();
/*返回当前节点的根节点*/
private int find(int x);
}
2、存储数据结构
如何表示节点与节点之间的连通性关系呢?
- 如果p和q连通,则他们有相同的根节点
用数组parent[]表示这种关系
- 如果自己就是根节点,那么parent[i]=i,即自己指向自己
- 如果自己不是根节点,则parent[i] == root id;
private int count ;
private int[] parent;
//构造函数
public UF (int n){
this.count = n;
parent = new int[n];
for(int i = 0;i < n;i++
{
//最初,每个节点均是独立的
parent[i] = i;
}
}
Union方法
介绍了存储的数据结构,将其中任意一个节点的根节点指向另一个节点的根节点即可;
//伪代码
public void unin(int p,int q){
//找到p的根节点root;
//找到q的根节点root;
//如果已经在同一个连通分中,跳过
//parent[rootP] = rootQ;
//或parent[rootQ] = rootP;
将问题转化成了如何快速找到某一个节点的根节点!!
通过数据结构parent的特点,根节点自己指向自己
private int find(int x){
while (x != parent[x]){
x = parent[x];
}
}
connected() && count()
实现代码
public bool connected(int p,int q){
int rootP = find(p);
int rootQ = find(q);
return rootQ == rootP;
}
count()需要维护一个全局变量,来记录图的连通分量的数量
另外,我们需要明确的是:只有在调用union()方法的时候,才可能改变连通分量的数量
public void union(int p,int q){
int rootP = find(p);
int rootQ = find(q);
if(rootP== rootQ) return ;
parent[rootP] = rootQ;
//联通分量 -1
count --;
}
public int count (){
return this.count;
}
瓶颈分析
从时间复杂度来讲,find()是决定并查集时间复杂度的重要因素。
对于有n个节点1个连通分量的并查集来说,最坏的时间复杂度为 O ( n ) O(n) O(n),最好的时间复杂度为 O ( 1 ) O(1) O(1).
- 最坏情况:全部只有左孩子,即根节点有n-1个孩子。
优化角度1:平衡性优化
思路:当我们每次连接两个节点的时候,不希望出现投中脚轻的情况。使用额外的一个数组size[]记录每个连通分量的中节点数,每次均把节点数少的分量接到节点数较多的分量上。

只有每个连通分量的根节点的size[]才可以代表该连通分量中的节点数
private int count;
private int parent[];
private int size[];
//构造函数
public UF (int n){
this.count = n;
parent = new int[n];
size = new int[n];
for(int i = 0;i < n;i++){
parent[i] = i;
//最初每个连通分量的个数均为1
size[i] = 1;
}
}
public void unoin(int p,int q){
int rootP = find(p);
int rootQ = find(q);
if(rootP == rootQ) return ;
/******修改部分******/
if(size[rootP] < size[rootQ]){
parent[rootP] = rootQ;
size[rootQ] += size[rootP];
}else{
parent[rootQ] = rootP;
size[rootP] += size[rootQ];
}
/******end*******/
count --;
}
优化角度2: 路径压缩
思路:使树高始终保持为常数
private int find(int x){
while (parent[x] != x){
//进行路径压缩
parent[x] = parent[parent[x]];
x = parent[x];
}
return x;
完整模板:
class UF{
private:
int count;
int parent[];
int size[];
public:
UF (int n){
this.count = n;
parent = new int[n];
size = new int[n];
for (int i = 0;i < n;i++){
parent[i] = i;
size[i] = 1;
}
}
void unoin(int p,int q){
int rootQ = find(q);
int rootP = find(p);
if(rootQ == rootP) return ;
// 平衡性优化
if (size[rootP] < size[rootQ]) {
parent[rootP] = rootQ;
size[rootQ] += size[rootP];
} else {
parent[rootQ] = rootP;
size[rootP] += size[rootQ];
}
this.count--;
}
bool conneted(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
return rootP == rootQ;
}
int count() {
return this.count;
}
int find(int x) {
while (x != parent[x]) {
// 路径压缩
parent[x] = parent[parent[x]];
x = parent[x];
}
return x;
}
}
实战题目
题目1 :被围绕的区域,题目详情可见被围绕的区域
public void solve(char[][] board){
int m = board.length;
int n = board[0].length;
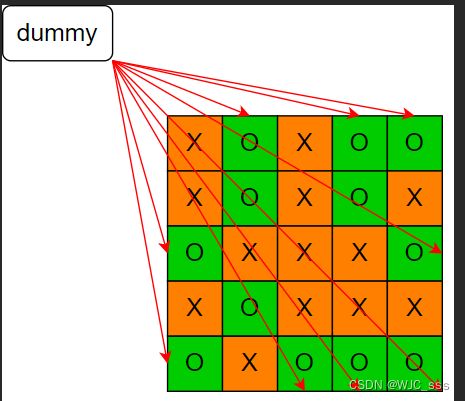
// 多一个节点用来存放 dummy
UF uf = new UF(m * n + 1);
int dummy = m * n;
// 将 dummy 和四条边的所有 'O' 相连
for (int i = 0; i < m; i++) {
if (board[i][0] == 'O') uf.union(dummy, i * n);
if (board[i][n - 1] == 'O') uf.union(dummy, i * n + n - 1);
}
for (int j = 0; j < n; j++) {
if (board[0][j] == 'O') uf.union(dummy, j);
if (board[m - 1][j] == 'O') uf.union(dummy, (m - 1) * n + j);
}
// 将内圈的所有相邻的 'O' 全部连起来
int[][] dirs = new int[][]{{1, 0}, {0, 1}, {0, -1}, {-1, 0}};
for (int i = 1; i < m - 1; i++) {
for (int j = 1; j < n - 1; j++) {
if (board[i][j] == 'O') {
for (int[] d : dirs) {
int newI = i + d[0];
int newJ = j + d[1];
if (board[newI][newJ] == 'O') {
uf.union(i * n + j, newI * n + newJ);
}
}
}
}
}
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (board[i][j] == 'O' && !uf.connected(dummy, i * n + j)) board[i][j] = 'X';
}
}
}
参考https://leetcode.cn/problems/longest-consecutive-sequence/solution/by-lfool-jdy4/