HDU 1372 Knight Moves

地址：http://acm.hdu.edu.cn/showproblem.php?pid=1372

思路：求“马”从一点到另一点的最短距离，马走日，BFS即可

分析：广度优先搜索题

题意如图所示：一个棋子（骑士）可以有八个方向走，广搜确定最小的走的步数。

 

代码如下：

 1 #include <iostream>

 2 #include <stdio.h>

 3 #include <string.h>

 4 #include <queue>

 5 using namespace std;

 6 int c[9][9];

 7 int dir[8][2] = {{-2,-1},{-2,1},{-1,2},{1,2},{2,1},{2,-1},{1,-2},{-1,-2}};

 8 typedef struct

 9 {

10     int x,y,count;

11 }node;

12 node start,finish;

13 int bfs()

14 {

15     memset(c,0,sizeof(c));

16     node pre,cur;

17     start.count = 0;

18     queue<node> q;

19     q.push(start);

20     c[start.x][start.y] = 1;

21     while(!q.empty())

22     {

23         pre = q.front();

24         q.pop();

25         if(pre.x == finish.x&&pre.y == finish.y)

26         return pre.count;

27         for(int i = 0; i < 8; i++)

28         {

29             cur.x = pre.x + dir[i][0];

30             cur.y = pre.y + dir[i][1];

31             if(cur.x<1||cur.x>8||cur.y<1||cur.y>8)continue;

32             if(c[cur.x][cur.y]==1)continue;

33             c[cur.x][cur.y] = 1;

34             cur.count = pre.count + 1;

35             q.push(cur);

36         }

37     }

38     return -1;

39 }

40 int main()

41 {

42     char row,end;

43     int col,ed;

44     int min;

45     while(scanf("%c",&row)!=EOF)

46     {

47         scanf("%d",&col);

48         getchar();

49         scanf("%c%d",&end,&ed);

50         getchar();

51         start.x = row-'a'+1;

52         start.y = col;

53         finish.x = end-'a'+1;

54         finish.y = ed;

55         if(start.x==finish.x&&start.y==finish.y)

56         min = 0;

57         else  min = bfs();

58         printf("To get from %c%d to %c%d takes %d knight moves.\n",row,col,end,ed,min);

59     }

60     return 0;

61 }

1．由原始问题引出的3个问题

（1）求任意两点间的最短步数

该问题不需要求出该两点间的路径上的点，也不需要求出拥有该最短步数的路径个数，只需将其间的最短步数求出即可；

（2）求任意两点间的所有最短路径及其全部信息

路径信息：路径上的每一点

该问题不仅需要求出两点间的最短路径，且要求出这样的最短路径有多少条和每一条路径上的每一点

（3）骑士周游世界问题

在一个8×8的方格棋盘中，按照国际象棋中马的行走规则从棋盘上的某一方格出发，开始在棋盘上周游，如果能不重复地走遍棋盘上的每一个方格，这样的一条周游路线在数学上被称为国际象棋盘上汉密尔顿链，求从任意一点出发，所有这样的汉密尔顿链及其全部信息；

 

 

2．问题分析

（1）棋盘的表示方法

可以用一个9×9的二维数组chess[9][9]来表示国际象棋的棋盘，在马还没有开始行走时，棋盘上所有的格都置为零，以后，马跳到哪个格，就将马跳跃的步数加1后的值记录在相应的空格里；开始点在行走前设为1；

注：为表示方便，取9×9，数组均下标从1开始；

 

（2）马的跳跃方向

在国际象棋的棋盘上，一匹马共有8个可能的跳跃方向，如图1所示，按顺时针分别记为1~8，设置一组坐标增量来描述这8个方向；

 

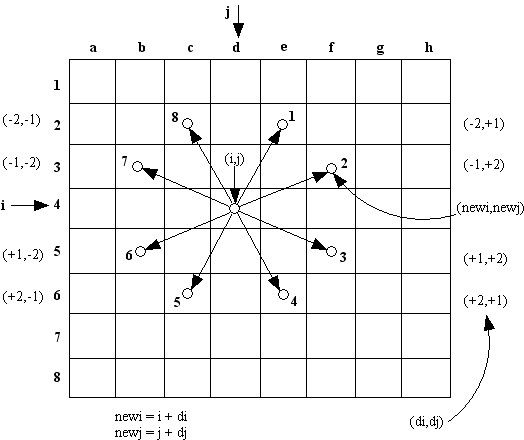
（3）马的跳跃方向的表示

设i表示行，j表示列，行增量为di，列增量为dj，设马向某个方向试探性地跳跃一步之后的新坐标为(newi,newj)，则有：

newi = i + di

newj = j + dj

其每个方向的增量如图所示，表示为(di,dj)

 

（4）基本过程

设当前点(i,j)，方向k，沿方向k跳一步后的新点(newi,newj)；每走一步，都要判断新点(newi,newj)是否还在棋盘上：

若1£newi£8且1£newj£8，则新点仍在棋盘上，则还需判断该点是否已经走过，即

若chess[newi][newj]=0，表示该步可走；

若chess[newi][newj]=1，表示该点已经走过，不能再走，放弃当前方向，并转向下一个方向试探；

否则，直接放弃当前方向，并转向下一个方向试探；

 

（5）有关两点间最短路径的定义

最短路径步数minstep：马跳的次数

拥有该步数的路径个数minstepcount：这样的路径有minstepcount条

最短路径上的点：每一条拥有该步数的路径上的点

knight 在点(i,j) 沿着 k 方向走一步,到达新点 (newi,newj)

i    : 走一步前的行下标 (i>=1 and i<=8)

j    : 走一步前的列下标 (j>=1 and j<=8)

k    : 方向 (k>=1 and k<=8)

newi : 走一步后的行下标 (newi>=1 and newi<=8)

newj : 走一步后的列下标 (newj>=1 and newj<=8)

 

3．求解算法

算法1：找出从S出发到达D的所有路径长度小于6的路径，然后再从这些路径中寻找最短路径

算法2：基于1的思想，但在搜索的过程中就开始求最短路径的长度，用变量代替回溯的值，若当前搜索的点已经超过当前最短路径长度，则从这个点回溯，从点出发的8个方向均不需要搜索，即在搜索树中，该点的儿子节点直接跳过；

注意：采用的算法不同，其数据结构就不同。