简单粗暴PyTorch之优化器
优化器
- 一、优化器属性与方法
- 二、pytorch中的优化器
一、优化器属性与方法
pytorch的优化器:
管理并更新模型中可学习参数的值,使得模型输出更接近 真实标签
导数:函数在指定坐标轴上的变化率
方向导数:指定方向上的变化率
梯度:一个向量,方向为方向导数取得最大值的方向

基本属性
• defaults:优化器超参数
• state:参数的缓存,如momentum的缓存
• params_groups:管理的参数组,list中有个字典
• _step_count:记录更新次数,学习率调整中使用
基本方法
• zero_grad():清空所管理参数的梯度
pytorch特性:张量梯度不自动清零

• zero_grad():清空所管理参数的梯度
• step():执行一步更新
• zero_grad():清空所管理参数的梯度
• step():执行一步更新
• add_param_group():添加参数组

• zero_grad():清空所管理参数的梯度
• step():执行一步更新
• add_param_group():添加参数组
常用在优化器参数的保存与加载
• state_dict():获取优化器当前状态信息字典
• load_state_dict() :加载状态信息字典

学习率(learning rate):
控制更新的步伐
Momentum(动量,冲量):
结合当前梯度与上一次更新信息,用于当前更新
让更新保持一个惯性
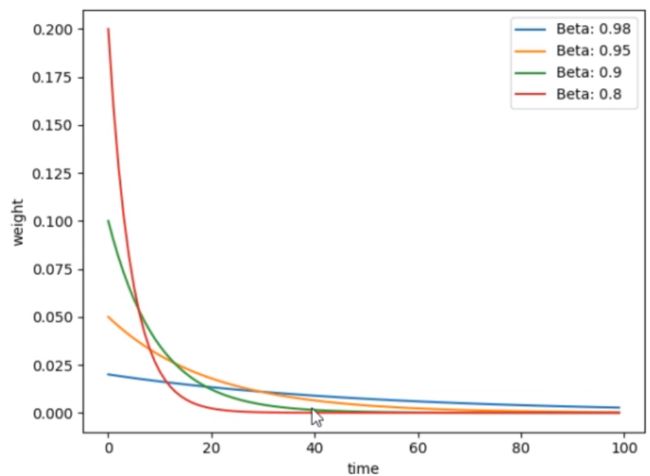
指数加权平均: v t = β ∗ v t − 1 + ( 1 − β ) ∗ θ t v 100 = β ∗ v 99 + ( 1 − β ) ∗ θ 100 = ( 1 − β ) ∗ θ 100 + β ∗ ( β ∗ v 98 + ( 1 − β ) ∗ θ 99 ) = ( 1 − β ) ∗ θ 100 + ( 1 − β ) ∗ β ∗ θ 99 + ( β 2 ∗ v 98 ) = ( 1 − β ) ∗ θ 100 + ( 1 − β ) ∗ β ∗ θ 99 + ( 1 − β ) ∗ β 2 ∗ θ 98 + ( β 3 ∗ v 97 ) = ( 1 − β ) ∗ β 0 ∗ θ 100 + ( 1 − β ) ∗ β 1 ∗ θ 99 + ( 1 − β ) ∗ β 2 ∗ θ 98 + ( β 3 ∗ v 97 ) 得到通式: = ∑ i N ( 1 − β ) ∗ β i ∗ θ N − i \begin{array}{l} \text { 指数加权平均: } \quad \mathrm{v}_{t}=\beta * v_{t-1}+(1-\beta) * \theta_{t} \\ \mathrm{v}_{100}=\beta * v_{99}+(1-\beta) * \theta_{100} \\ =(1-\beta) * \theta_{100}+\beta *\left(\beta * v_{98}+(1-\beta) * \theta_{99}\right) \\ =(1-\beta) * \theta_{100}+(1-\beta) * \beta * \theta_{99}+\left(\beta^{2} * v_{98}\right) \\ =(1-\beta) * \theta_{100}+(1-\beta) * \beta * \theta_{99}+(1-\beta) * \beta^{2} * \theta_{98}+\left(\beta^{3} * v_{97}\right) \\ =(1-\beta) * \beta^{0}* \theta_{100}+(1-\beta) * \beta^{1} * \theta_{99}+(1-\beta) * \beta^{2} * \theta_{98}+\left(\beta^{3} * v_{97}\right) \\ \text{得到通式:}\\ =\sum_{i}^{N}(1-\beta) * \beta^{i} * \theta_{N-i} \end{array} 指数加权平均: vt=β∗vt−1+(1−β)∗θtv100=β∗v99+(1−β)∗θ100=(1−β)∗θ100+β∗(β∗v98+(1−β)∗θ99)=(1−β)∗θ100+(1−β)∗β∗θ99+(β2∗v98)=(1−β)∗θ100+(1−β)∗β∗θ99+(1−β)∗β2∗θ98+(β3∗v97)=(1−β)∗β0∗θ100+(1−β)∗β1∗θ99+(1−β)∗β2∗θ98+(β3∗v97)得到通式:=∑iN(1−β)∗βi∗θN−ibeta越小记忆周期越短
原始梯度下降公式: w i + 1 = w i − l r ∗ g ( w i ) w_{i+1}=w_{i}-l r * g\left(w_{i}\right) wi+1=wi−lr∗g(wi)
pytorch中更新公式: v i = m ∗ v i − 1 + g ( w i ) w i + 1 = w i − l r ∗ v i \begin{array}{c} v_{i}=m * v_{i-1}+g\left(w_{i}\right) \\ w_{i+1}=w_{i}-l r * v_{i} \end{array} vi=m∗vi−1+g(wi)wi+1=wi−lr∗vi
+:第i+1次更新的参数
lr:学习率
:更新量
m:momentum系数
(): 的梯度
eg: v 100 = m ∗ v 99 + g ( w 100 ) = g ( w 100 ) + m ∗ ( m ∗ v 98 + g ( w 99 ) ) = g ( w 100 ) + m ∗ g ( w 99 + m 2 ∗ v 98 = g ( w 100 ) + m ∗ g ( w 99 ) + m 2 ∗ g ( w 98 ) + m 3 ∗ v 97 \begin{aligned} v_{100} &=m * v_{99}+g\left(w_{100}\right) \\ &=g\left(w_{100}\right)+m *\left(m * v_{98}+g\left(w_{99}\right)\right) \\ &=g\left(w_{100}\right)+m * g\left(w_{99}+m^{2} * v_{98}\right.\\ &=g\left(w_{100}\right)+m * g\left(w_{99}\right)+m^{2} * g\left(w_{98}\right)+m^{3} * v_{97} \end{aligned} v100=m∗v99+g(w100)=g(w100)+m∗(m∗v98+g(w99))=g(w100)+m∗g(w99+m2∗v98=g(w100)+m∗g(w99)+m2∗g(w98)+m3∗v97
二、pytorch中的优化器
- optim.SGD
pytorch中最常用也是最实用的优化器
主要参数:
• params:管理的参数组
• lr:初始学习率
• momentum:动量系数,贝塔
• weight_decay:L2正则化系数
• nesterov:是否采用NAG
optim.SGD(params, lr=<object object>, momentum=0,
dampening=0, weight_decay=0, nesterov=False)
- optim.Adagrad:自适应学习率梯度下降法
- optim.RMSprop: Adagrad的改进
- optim.Adadelta: Adagrad的改进
- optim.Adam:RMSprop结合Momentum,
《Adam: A Method for Stochastic Optimization》 - optim.Adamax:Adam增加学习率上限
- optim.SparseAdam:稀疏版的Adam
- optim.ASGD:随机平均梯度下降
- optim.Rprop:弹性反向传播
- optim.LBFGS:BFGS的改进