VAE的原理+直观理解+公式推导+去噪+异常检测
1、VAE原理的直观理解
使用(VAE)生成建模,理解可变自动编码器背后的数学原理
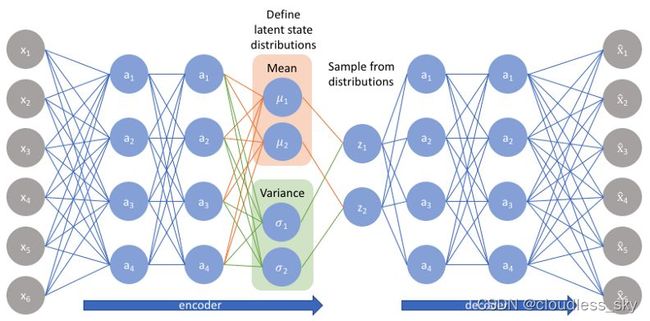


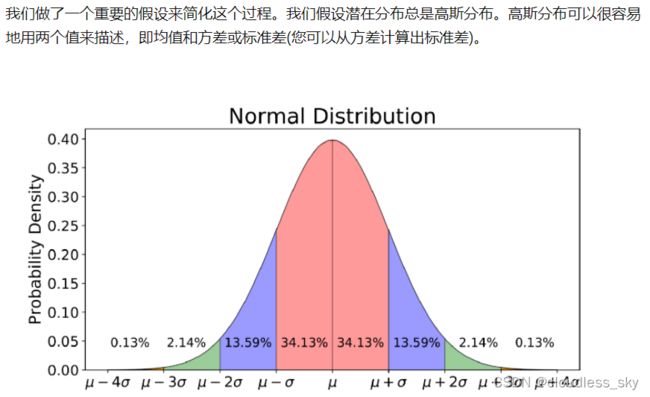
一般设先验分布为标准正态分布,但是也可以是其他分布。

KL项目的是使得q(z|x)与p(z|x)相似,只是后面ELBO经过推导转换成了q(z|x)和p(z)尽可能靠近的问题。

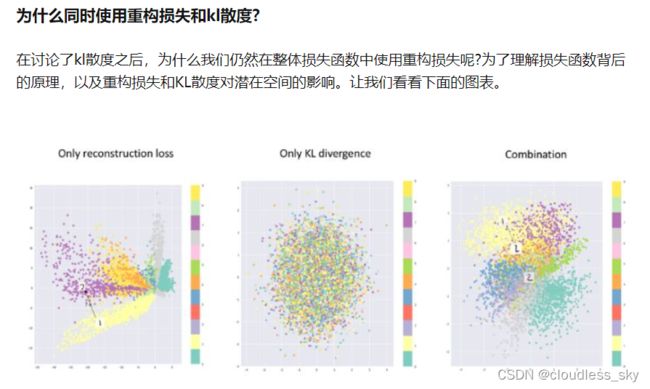


基于序列的VAE生成模型
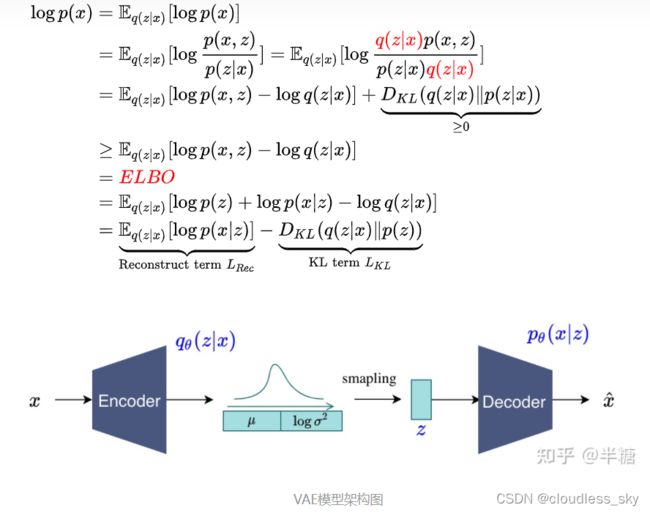
变分自编码器VAE:原来是这么一回事 | 附开源代码
VAE希望训练一个模型 X=g(Z),这个模型能够将原来的概率分布映射到训练集的概率分布,也就是说,它的目的都是进行分布之间的变换。


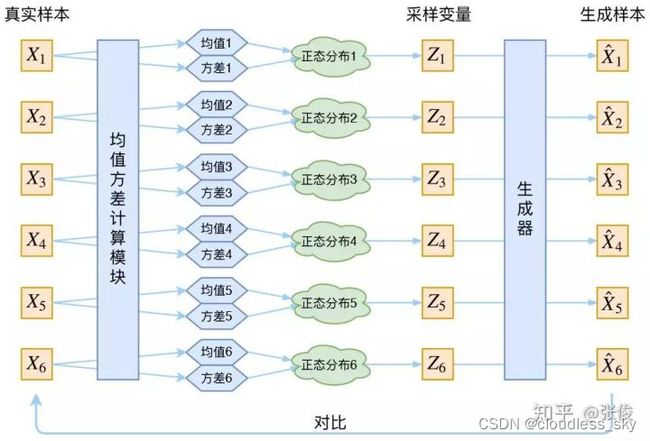
对于这张图,我感到疑惑。AE是降维,比如一张人脸图片X(一个列向量)的潜在空间Z是几个表示提取的特征的正态分布,X到Z显然是降维了;但是按照这张图的说法,每个x对应一个正态分布Z(两个参数),如果x是个图片,那就是只提取了一个特征用来表示这张图片?
如果X是个窗口为W的序列,那也是只提取一个序列的整体特征来重构它?—所以Unsupervised Anomaly Detection via Variational Auto-Encoder for Seasonal KPIs in Web Applications对于VAE能够异常检测的解释是VAE可以学习到序列整体的正常模式,但是很可能会因为维度的缩减而丢失掉异常点的特征,所以重构出来的xt……xt+w接近于正常的数据,可以用来和输入序列中的异常相比。
还有一些多元时间序列论文中是step-wise,也就是每个xt对应一个zt,但是这个xt并不是一个单值,而是D维度的一个向量,因为有D个传感器,而时间步之间的依赖则利用LSTM或者GRU去学习;另一些是block_wise,即每一个sensor的长度为W的序列对应一个VAE,如果每个VAE中的前向网络是LSTM或GRU的话,那么也能够学习时间依赖,只是无法学习sensors之间的关系了。
首先,我们希望重构 X,也就是最小化 D(X̂k,Xk)^2,但是这个重构过程受到噪声(这个噪声指的是不同于AE中直接把X编码成Z,而是编码成一个高斯分布,从高斯分布中采样就未必可以取到均值)的影响,因为Zk 是通过重新采样过的,不是直接由 encoder 算出来的。采样的过程中运用了重采样技巧,在Z的均值的基础上加了个从标准正态分布中采样的方差,便于反向梯度传播。显然噪声会增加重构的难度,不过好在这个噪声强度(也就是方差)通过一个神经网络算出来的,所以最终模型为了重构得更好,肯定会想尽办法让方差为0(试想一下,类似AE的情况,X被映射到Z分布,均值就是最能代表X的值,重构效果最好)。而方差为 0 的话,也就没有随机性了,所以不管怎么采样其实都只是得到确定的结果(也就是均值)。
说白了,模型会慢慢退化成普通的 AutoEncoder,噪声不再起作用。
这样不就白费力气了吗?说好的生成模型呢?
别急别急,其实 VAE 还让所有的 p(Z|X) 都向标准正态分布看齐,这样就防止了噪声为零,同时保证了模型具有生成能力。
怎么理解“保证了生成能力”呢?如果所有的 p(Z|X) 都很接近标准正态分布 N(0,I),那么根据定义:
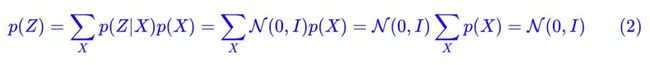
**为了使模型具有生成能力,VAE 要求每个 p(Z|X) 都向标准正态分布看齐。**那怎么让所有的 p(Z|X) 都向 N(0,I) 看齐呢?
原论文直接算了一般(各分量独立的)正态分布与标准正态分布的 KL 散度KL(N(μ,σ^2)‖N(0,I))作为这个额外的 loss,计算结果为:

这里的 d 是隐变量 Z 的维度,而 μ(i) 和 σ_{(i)}^{2} 分别代表一般正态分布的均值向量和方差向量的第 i 个分量。
这个 loss 可以分两部分理解:

从上式也可以看出,生成均值和方差的是不同的神经网络,有不同的参数。在 VAE 中,它的 Encoder 有两个,一个用来计算均值,一个用来计算方差。
KL具体推导:

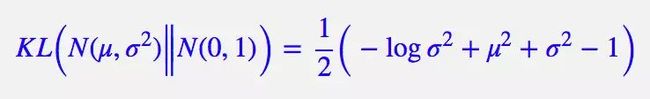
说白了,重构的过程是希望没噪声的,而 KL loss 则希望有高斯噪声的,两者是对立的。
深度学习-李宏毅GAN学习之VAE
关于VAE中的采样问题:
推断网络把高维的X映射到低维的Z,这个Z一般是个高斯混合分布,有几个分布就有几对均值方差参数,至于这个Z究竟是几维(几个混合分布)的,那就是自己规定的K。从Z分布中采样,采样几次呢?比如人脸图片的那个采样似乎是从每个Z分布中取一个点(从q(z;f(x,φ))中采样)(特征),最终经过解码构成一个完整的图片的向量表示。那么就是Z是几维(有几个分布)就采样几次。但是据上面这篇博客分析,每个X对应一个Z,重构出一个X,那么只需要采样一次就好。最终的X自然是由每一个重构的Xi组成的。采样得到Z也就可以送入解码器,训练得到解码器P(x|z)的参数,采样多少个Z就有多少个p(x|z),想要得到重构的X^,则从p(x|z)中抽样得到,一般取均值即可。
而似然考虑的是从采样得到的Z中重构x的概率,也就是p(x|z)是个高斯分布,多个点的概率高斯分布堆叠起来就是个混合高斯分布。


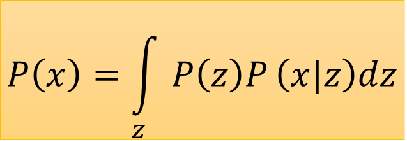
其中,q(z|x)和p(x|z)的参数都是用神经网络学到的。

本质上就是用自编码器去产生很多高斯分布,去拟合样本的分布,然后某个x对应的高斯分布里采样z,然后复原成x。这个是完全去模仿分布,只能生成数据中已有的图片,很难创造新的图片,最多也就是插值图片了。也可以理解成图片的特征向量z采样于某种高斯分布,我们要把他给找出来,我们希望这个分布贴近标准正太分布,然后通过编码器生成对应均值和方差,然后采样z,希望z又能复原图片,这样就找到了这个z背后的高斯分布。
图像去噪的自动编码器
自动编码器由两个连接的人工神经网络组成: 编码器模型和解码器模型。自动编码器的目标是找到一种将输入图像编码成压缩形式(也称为潜在空间)的方法,使得解码后的图像版本尽可能接近输入图像。下面的网络提供了原始图像 x,以及它们的噪声版本 x ~ 。网络试图重建它的输出 x’尽可能接近原始图像 x,通过这样做,它学会了如何对图像进行去噪。

如图所示,编码器模型将输入转换为小的密集表示。解码器模型可以看作是能够生成特定特征的生成模型。
编码器和解码器网络通常作为一个整体进行训练。损失函数惩罚网络以创建与原始输入 x 不同的输出 x’。
通过这样做,编码器学会在潜在空间中保存尽可能多的相关信息,尽可能的去除不相关部分(例如噪声)。解码器则学习获取潜在空间的信息并将其重构为无错的输入。
AE为何能用于时间序列的异常检测?
基于自编码器的时间序列异常检测算法
自编码器(Auto Encoder)也是一种无监督的数据压缩算法,或者说特征提取算法。其目标函数就是为了拟合一个恒等函数。并且编码器和解码器都是前馈神经网络。对于自编码器而言,它的输入层的维度等于输出层的维度,隐藏层的维度是需要小于输入层的维度的。只有这样,自编码器才可以学习到数据分布的最显著特征。对于自编码器而言,其本质上也是一个神经网络,那么它的激活函数其实不仅可以选择 sigmoid, 还可以使用 tanh,ReLU,LeakyReLU 等其余激活函数,其本质上都是为了拟合一个恒等变换,中间层则作为一个特征提取的工具。在训练的时候,同样是使用反向传播算法,可以使用不同的优化函数,例如 SGD,Momentum,AdaGrad,RMSProp,Adam 等。

在图像领域,有学者尝试使用自编码器来进行图像的重构工作,图像的特征提取等内容,整体来看也能达到不错的效果,请看下图:

从上图来看,基于均方误差的自编码器是无法重构出乒乓球的。由于该自编码器的容量有限,目标函数是均方误差,因此自编码器并没有意识到乒乓球是图片中的一个重要物品。那么根据异常检测的观点来看,小乒乓球其实就可以作为图片中的异常点。只要在图片的局部,重构出来的图片和之前的图片存在着巨大的误差,那么原始图片上的点就有理由认为是异常点。
在这个思想下,针对时间序列异常检测而言,异常对于正常来说其实是少数。如果我们使用自编码器重构出来的时间序列跟之前有所差异的话,其实我们就有理由认为当前的时间序列存在了异常。



VAE与GAN做异常检测的原理
近几年,有大量的人用VAE和GAN来做异常检测,用这两个模型做异常检测的假设都是一样的,即假定正常数据是服从某一种分布的,而异常数据是不能够拟合进这个分布的,因此我们可以用VAE和GAN来找到正常数据的分布,从而用这个分布来做异常检测。
1、VAE
VAE是变分自编码器的简称,该模型最开始提出的目的是为了找到训练数据的分布,从而用这个分布来生成数据。从另一个角度而言,如果我们能够找到正常数据的分布,那么我们就可以用这个分布来做异常检测。具体来说,我们在训练数据上训练好一个VAE,该VAE的encoder能够将输入数据X映射到隐变量Z,decoder将隐变量Z再映射回X,当我们训练好一个VAE之后,如果我们输入一个异常数据,该模型很大概率会将该异常数据重构成一个正常数据(因为原始数据经过降维之后,异常特征很可能被丢掉),因此我们就可以判别输入数据是否是一个正常数据。用一句话概括,就是正常数据重构成正常数据的概率会很高,而异常数据重构成异常数据的概率会很低,而且一般来说我们输入一个异常数据,VAE也会将其重构成一个正常数据。
2、GAN
GAN做异常检测的原理和VAE是一样的,只不过这两者得到正常数据的分布的方式不同,VAE通过变分推断来得到训练数据的分布,而GAN直接使用生成器来模拟数据的分布,用判别器来判断生成器模拟的分布的好坏。
这两者都可以用来做异常检测,也都是基于训练数据的分布,但是VAE的鲁棒性比GAN更好,但是GAN在调优之后效果比VAE更好。
经典论文:Unsupervised Anomaly Detection via Variational Auto-Encoder for Seasonal KPIs in Web Applications
这篇论文研究的是单时间序列异常检测,以滑动窗口长度为W的时间序列作为VAE的输入,输出也是W长的序列;
The philosophy is to focus on normal patterns instead of anomalies. Roughly speaking, they all first recognize “normal” regions in the original or some latent feature space,and then compute the anomaly score by measuring “how far” an observation is from the normal regions.
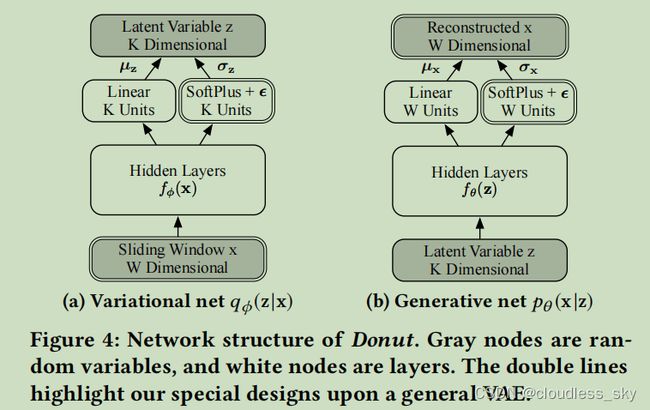
对于部分异常的x4,降维将使甜甜圈能够识别其正常模式˜x,并使qϕ(z|x)约为qϕ(z|˜x)。这种影响是由以下原因引起的。训练甜甜圈以最大的努力重建训练样本中的正常点,而降维则使甜甜圈只能从x中捕获少量的信息。因此,只有整体形状被编码为qϕ(z|x)。异常信息在此过程中很可能被丢弃。然而,如果一个x太异常,甜甜圈可能无法识别任何正常的˜x,因此qϕ(z|x)就会变得不明确。



上图运用了蒙特卡罗方法从Z中抽样L次,分别重构序列X,L次的期望就是ELBO的第二项重构概率。
下面是一篇针对这篇论文的分析博客。
AIOps探索:基于VAE模型的周期性KPI异常检测方法——VAE异常检测
VAE也实现了跟AutoEncoder类似的作用,输入一个序列,得到一个隐变量(从隐变量的分布中采样得到),然后将隐变量重构成原始输入。不同的是,VAE学习到的是隐变量的分布(允许隐变量存在一定的噪声和随机性),因此可以具有类似正则化防止过拟合的作用。基于VAE的周期性KPI异常检测方法其实跟AutoEncoder基本一致,可以使用重构误差来判断异常,下面是结果,上图是原始输入,下图是重构结果。我们检测异常是通过对比重构后的结果与原始输入的差距,通过设置异常阈值来判断是否异常。
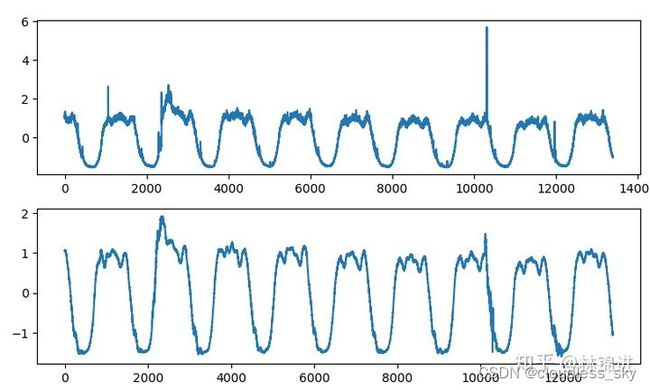
可以看出,输入序列的异常处经过重构被减轻甚至消失(降维丢失部分特征),我们认为重构出来的为近似正常数据,和原始带有异常的数据做差,差距大的地方就是异常。
论文2015:Variational Autoencoder based Anomaly Detection using Reconstruction Probability
AE:

基于自动编码器的异常检测是一种基于半监督学习的基于偏差的异常检测方法。它使用重构误差作为异常评分。具有高重建度的数据点被认为是异常的。只有具有正常实例的数据才被用于训练自动编码器。经过训练后,自动编码器将很好地重构正常数据,而自动编码器没有遇到的异常数据。算法2显示了利用自动编码器重构误差的异常检测算法。
输入和输出为长度为N的数据X;


VAE:

VAE的目标是最大化数据的边际似然值,(p(x)属于0~1越大,即log为负越大,说明重构效果越好),

单个点的边际似然为:
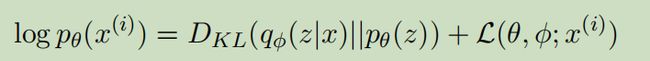
方程右边的第一项是近似后验和先验的KL散度。方程右边的第二项是数据点i的边际似然值上的变分下界。
由于KL总是大于0,上式可以写成

于是,最大化边际似然的问题转换为最大化最大化变分下界ELBO,而ELBO又包括两项。第一项是潜在可变z的近似后验和先验之间的KL散度,此项迫使后验分布类似于先验分布,作为一个正则化项。第二项可以理解为通过后验分布qφ(z|x)和似然pθ(x|z)重建x。
VAE利用神经网络对近似后验qφ(z|x)的参数进行建模。这是VAE可以与自动编码器相关联的地方。如图2所示,在自动编码器的类比中,近似的后验qφ(z|x)是编码器,有向概率图形模型pθ(x|z)是解码器。值得强调的是,VAE建模的是分布的参数,而不是值本身。也就是说,编码器中的f(x,φ)输出近似后验qφ(z|x)的参数,要获得潜在变量z的实际值,需要从q(z;f(x,φ))中采样。因此,VAE的编码器和解码器可以被称为概率编码器和解码器。f(x,φ)是一个神经网络,表示数据x和潜在变量z之间的复杂关系。为了得到重构ˆx,给定样本z,通过g(z,θ)得到pθ(x|z)的参数,其中重构ˆx从pθ(x;g(z,θ))中采样。总之,在VAE中建模的是分布参数,而不是值本身。对分布的选择适用于任何类型的参数分布。为本研究对象的分布潜变量z,即pθ(z)和qφ(z|x),常见的选择是各向同性正态,因为假设潜变量空间中变量之间的关系比原始输入数据空间要简单得多。可能性pθ(x|z)的分布取决于数据的性质。如果数据为二进制形式,则使用伯努利分布。如果数据是连续的形式,则使用多元高斯分布。z不一定要服从高斯分布,也可以是其他分布,不会有影响,因为我们的神经网络足够强大,只要通过学习,理论上可以表示任何函数。
VAE和自动编码器之间的主要区别是,VAE是一个随机生成模型,可以给出校准的概率,而自动编码器是一个没有概率基础的确定性判别模型。这很明显,VAE模拟了上述的分布参数。
反向传播用于训练VAE。此外,还运用了重参数化技巧。方程(7)上的第二项应该通过蒙特卡罗方法来计算。对于每个输入数据xi,需要采样L个Z来运用蒙特卡罗方法计算ELBO的第二项。但不要混淆,N个Xi只被映射到一个分布Z。采样L个Z只是为了在训练时求ELBO的第二项,在测试时计算重构概率(比ELBO第二项少了log,就是p(x)重构的平均概率)。

算法图中的只是单个数据Xi的重构概率;对于时间序列预测问题,我们要关注的就是单个时间步的重构概率。

异常检测任务采用半监督框架,仅使用正常实例的数据来训练VAE。概率编码器fφ和解码器gθ分别在潜在变量空间和原始输入变量空间中优化了各向同性正态分布。为了测试,从训练的VAE的概率编码器中提取一些样本。对于编码器中的每个样本,概率解码器输出均值和方差参数。利用这些参数,计算了从分布中生成原始数据的概率。平均概率被用作异常得分,被称为重建概率。这里计算的重建概率是Eqφ(z|x)(logpθ(x|z))的蒙特卡罗估计,这是方程(7)右边的第二项。重构概率高的数据点被划分为异常数据点。
利用推导出原始输入变量分布参数的随机潜变量计算重构概率。正在重建的是输入变量分布的参数,而不是输入变量本身。这本质上是从近似后验分布中提取的给定潜在变量所产生的数据的概率。由于从潜在变量分布中抽取了大量的样本,这使得重构概率可以考虑到潜在变量空间的可变性,这是所提出的方法与基于自编码器的异常检测之间的主要区别之一。可以使用适合于数据的输入变量空间的其他分布。对于连续数据,算法4可以采用正态分布。对于二进制数据,可以使用伯努利分布。在潜变量空间的分布情况下,最好采用简单的连续分布,如各向同性正态分布。
重构概率与自编码器的重构误差有两种不同。首先,潜在变量是随机变量。在自动编码器中,潜在变量被确定性映射去定义。然而,由于VAE使用概率编码器来建模潜在变量的分布,而不是潜在变量本身,因此可以从抽样过程中考虑潜在空间的可变性。与自动编码器相比,这扩展了VAE的表达能力,因为即使正常数据和异常数据可能共享相同的平均值,可变性也可能有所不同。推测异常数据将有较大的方差和较低的重建概率。由于自动编码器的确定性映射可以被认为是对dirac增量分布值的平均值的映射,因此自动编码器缺乏处理可变性的能力。
第二,重构是随机变量。重构概率不仅考虑了重构与原始输入之间的差值,而且还通过考虑分布函数的方差参数来考虑重构的变异性。这一特性使其对根据可变方差进行的重建具有选择性的敏感性。方差较大的变量可以容忍重构和原始数据的较大差异作为正常行为,而方差较小的变量可以显著降低重构概率。这也是自动编码器由于其确定性而缺乏的一个特性。
第三,重建是概率度量。基于自动编码器的异常检测将重构误差作为异常分数,如果输入变量是异构的,则难以计算。为了总结异构数据的差异,需要一个加权和。问题是,没有一种通用的客观方法来确定合适的权值,因为权值会根据您所拥有的数据而有所不同。此外,即使在确定了权值之后,确定重建误差的阈值也是很麻烦的。这将没有明确的客观门槛。相比之下,重构概率的计算不需要对异构数据的重构误差进行加权,因为每个变量的概率分布允许它们通过其自身的变异性分别计算。对于任何数据,1%的概率总是1%。因此,确定重构误差的阈值比重构误差的阈值更客观、更合理、更容易理解。
一些思考:
AE把一个长度为L的序列映射到M维的特征潜在表示,想象一下,假设编码器是简单的线性神经网络,那么M维中的每一个值可以看作是L个Xi值的加权求和,不同的权重得到不同的特征,比如人脸的眼睛,鼻子,嘴巴,Z中的每一维度都可以认为是一个特征,根据这些特征再去还原X。那么VAE呢?唯一不同的只是VAE的Z变成了概率分布,比如高斯分布,就用均值和方差来表示,一个L长度的序列对应“”“一个(并不是1个)”均值和方差,但这不仅仅是一个简单的高斯分布,而是混合高斯分布。同样地,想象一下,L个Xi映射出M个特征,每个特征对应一个高斯分布,这M个高斯分布是独立的,所以可以相乘得到最终的混合高斯分布,保存的参数,均值和方差的对数也有M对,这样看来,参数是AE的两倍。但是实际上的高斯分布波形只有一个,就是混合后的,而采样Z的时候也是从这一个波形里面采样出L个来重构X。
那么,AE为啥能够用来异常检测呢?训练中学到的正常模式是如何在测试中起作用的呢?
在训练中用的都是正常数据,通过不断的LOSS反向传播,编码器可以很好地捕捉到可以重构X的那些正常特征,也就是编码神经网络的参数W1矩阵(LXM尺寸)被训练好了,比如人脸,我知道怎么样的权重分配可以得到眼睛,鼻子这些特征了。现在我们把带有异常的测试数据送入编码器,比如其中一个Xi突然变很大,而它的权重W没变,经过加权会导致M个Zi都发生不同程度的变化(学到的眼睛鼻子变形了),而此时的解码器参数矩阵W2还是正常模式下的,这就会导致重构出来的整个X都误差较大(L个Xi中正常的因为Z的变化而不能很好地重构(把我眼睛鼻子的原材料整偏了),异常的因为没有W1无法使得它得到它的特征Z而无法很好地重构(我从丹凤眼变成了杏眼,你没捕捉到,而且重构的时候还用的原来的分配比例,重构出来就会啥也不太像))。迁移到时间序列问题,对于某个单元时间序列,[t-w,t]这个切片的所有的Xi重构误差都比较大,那整个切片得分较高,被视为异常段。我们称t时刻,第J个传感器异常。
再迁移到VAE,编码器表现为q(Z|X),本质上也有个W1矩阵,把X映射到M对均值和方差,构成混合高斯分布q(z|x),ELBO中的重构项引导者更加有效的重构,而正则化项使得q(z|x)和p(z)靠近。训练好之后,也就得到了q(z|x)和p(x|z),也就是得到了W1和W2,现在送入带有异常的测试数据,和AE道理相似,突如其来的异常波动我学不到你的特征(W1不变,调料变了,比例没变),所以尖端重构出来可能就平缓了,就导致异常点的重构概率小(重构效果不好),被视为异常。
注意,VAE的编码器和解码器网络经常被换成RNN或者GCN,此时,最终也都得经过两个线性神经网络,分别得到均值和方差,主要是实现维度的变换(L到M)。



