数据结构与算法——二叉树
二叉树
- 一、树的定义:
- 二、二叉树的概念
-
- 2.1二叉树的定义:
- 2.2二叉树的性质
- 2.3 二叉树的存储表示
- 2.4.二叉树的遍历(Binary Tree Traversal)
-
- 递归实现先、中、后序遍历:
- 构建二叉树:
- 非递归实现先、中、后序遍历
- 层次遍历:
- Z型层次遍历
- 数组形式存储,实现二叉树的中序遍历
- 2.5计算二叉树的结点个数和深度
- 三、二叉树的判定
-
- 3.1判断是否为满二叉树
- 3.2是否是完全二叉树
- 四、二叉树的查询
-
- 4.1在二叉树中查询Value值,如果存在返回结点的地址,否则返回空
- 4.2给定一个二叉树,找到该树中某个指定节点的双亲
一、树的定义:
树是由n个结点组成的优先级合。如果n=0,称为空树;如果n>0,则
- 有一个特定的称之为根(root)的结点,它只有直接后继,但没有直接前驱;
- 除根以外的其它结点划分为m(m>=0)个互不相交的有限集合T0,T1,…,Tm-1,每个集合又是一棵树,并且称为根的子树(subTree)。每棵子树的根结点有且仅有一个直接前驱,但可以有0个或多个直接后继。
- 结点的度:一个节点含有的子树的个数称为该节点的度。
- 树的度:一棵树中,最大节点的度称为树的度。
- 叶节点或终端节点:度为零的节点。
- 非终端节点或分支节点:度不为零的节点。
- 父亲节点或父节点:若一个节点含有子节点,则这个节点称之为其子节点的父节点;
- 孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点。
- 兄弟节点:具有相同父节点的节点互称为兄弟节点。
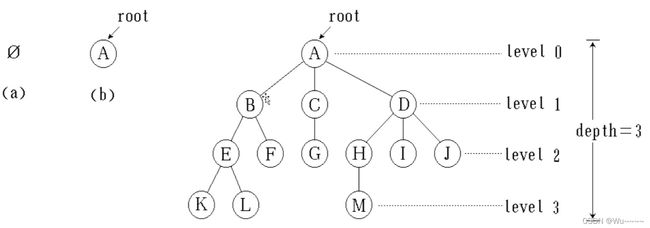
- 节点的层次:从根开始定义起,根为第一层,根的子节点为第二层,以此类推。
- 深度:对于任意节点n,n的深度为从根到n的唯一路径长,根的深度为0.
- 高度:对于任意节点n,n的高度为从n到一片树叶的最长路径长,所有树叶的高度为0.
- 堂兄弟节点:父节点在同一层的节点互为堂兄弟。
- 节点的祖先:从根到该节点所经分支上的所有结点。
- 子孙:以某节点为根的子树中任一节点都称为该节点的子孙。
- 森林:由m(m>=0)棵互不相交的树的集合称为森林。
- 树中任意节点的子节点之间没有顺序关系,这种树称为无序树,也成为自由树。反之是有序树。
二、二叉树的概念
2.1二叉树的定义:
一颗二叉树是结点的有限集合,该集合或者为空,或者是由一个根结点加上两棵分别称为左子树和右子树的互不相交的二叉树组成。
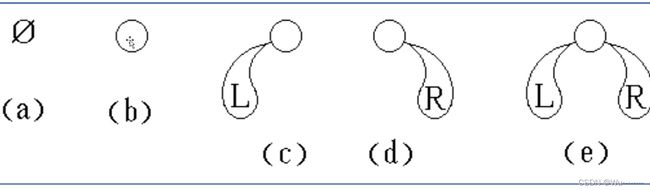
2.2二叉树的性质
- 若二叉树的层次从0开始,则在二叉树的第i层最多有2i个结点。(i>=0)
- 高度为k的二叉树最多有2^(k+1)-1个结点。(k>=-1)
- 对任何一棵二叉树,如果其叶结点个数为n0,度为2的非叶结点个数为n2,则有n0=n2+1。
定义:满二叉树(Full Binary Tree):每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。
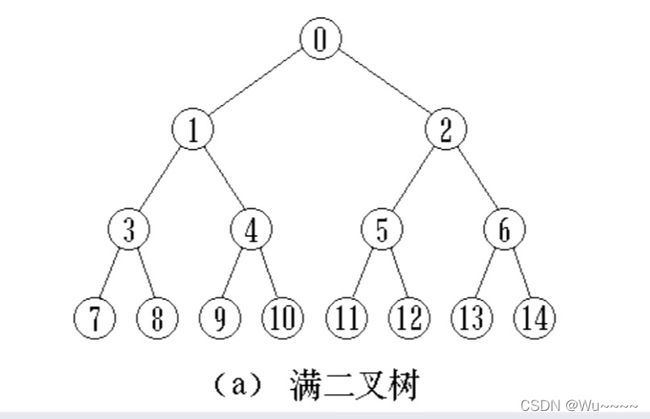
定义:完全二叉树(Complete Binary Tree):若设二叉树的高度为h,则共有h+1层。除第h层外。其他各层(0~h-1)的结点数都达到最大个数,第h层从右向左连续缺若干结点,这就是完全二叉树。
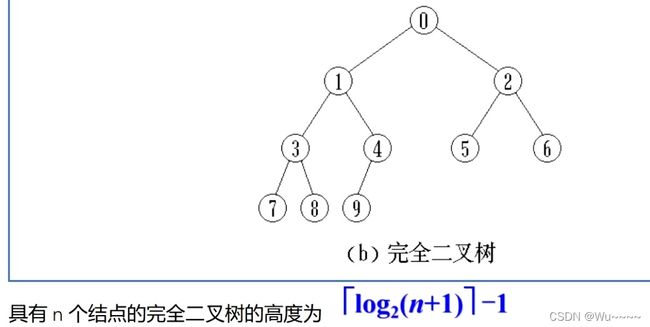

若左孩子是一颗满二叉树,右孩子是满二叉树,则这棵树不一定是满二叉树。
若左孩子是一颗完全二叉树,右孩子是完全二叉树,则这棵树不一定是完全二叉树。
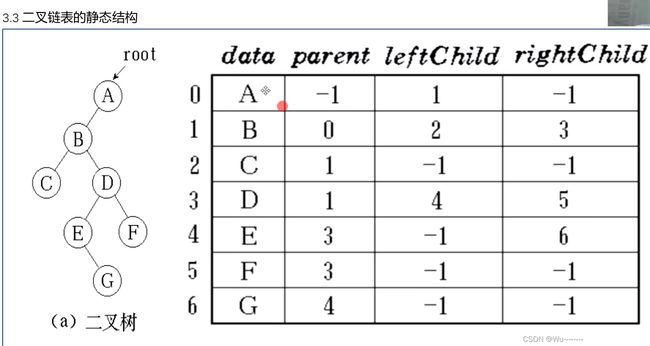
2.3 二叉树的存储表示
- 什么数据结构:Data_Structure=(D,S)。
- 数据的逻辑结构是对数据之间关系的描述,画图表示。
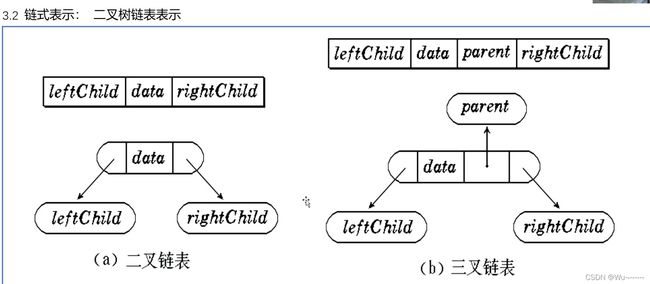
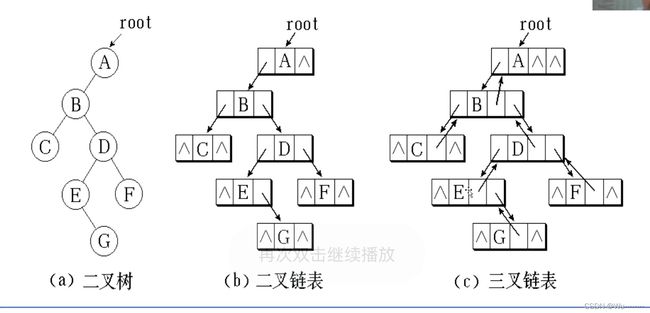
- 数据元素之间的关系有两种不同的表示方法:顺序映象和非顺序映象,并由此得到两种不同的存储结构:顺序存储结构和链式存储结构。数据的存储结构是指数据的逻辑结构在计算机中的表示。
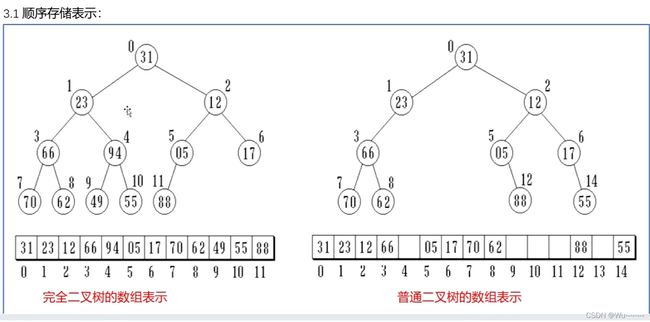
结点i,左孩子2i+1,右孩子2i+2。
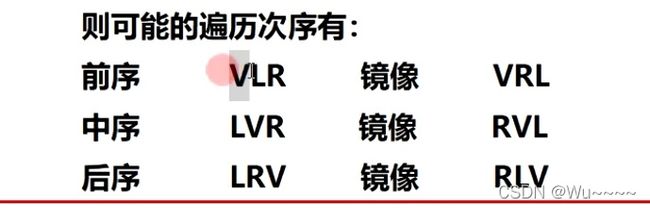
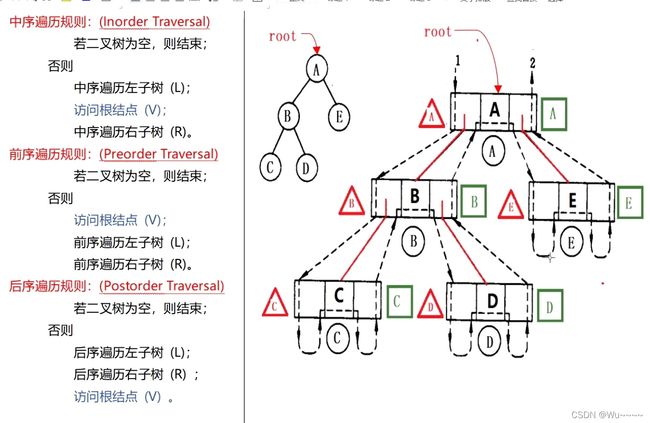
2.4.二叉树的遍历(Binary Tree Traversal)
所谓树的遍历,就是按某种次序访问树中的结点,要求每个节点访问一次且仅访问一次。
访问根节点记作V;遍历根的左子树记作L;遍历根的右子树记作R;
递归实现先、中、后序遍历:
typedef char ElemType;
typedef struct BtNode //BinaryTreeNode
{
ElemType data;
struct BtNode* leftchild;
struct BtNode* rightchild;
}BtNode,*BinaryTree;
//先序遍历
void PreOrder(BtNode* p)
{
if (p != NULL)
{
cout << p->data << " ";
PreOrder(p->leftchild);
PreOrder(p->rightchild);
}
}
//中序遍历
void InOrder(BtNode* p)
{
if (p != NULL)
{
InOrder(p->leftchild);
cout << p->data << " ";
InOrder(p->rightchild);
}
}
//后序遍历
void PastOrder(BtNode* p)
{
if (p != NULL)
{
PastOrder(p->leftchild);
PastOrder(p->rightchild);
cout << p->data << " ";
}
}
int main()
{
BinaryTree root = CBTree1();
PreOrder(root);
cout << endl;
InOrder(root);
cout << endl;
PastOrder(root);
cout << endl;
return 0;
}
构建二叉树:
BtNode* BuyNode()
{
BtNode* s = (BtNode*)malloc(sizeof(BtNode));
if (NULL == s)exit(1);
memset(s, 0, sizeof(BtNode));
}
//构建二叉树
BtNode* CBTree1()
{
BtNode* s = NULL;
ElemType elem;
cin >> elem;
if (elem != '#')
{
s = BuyNode();
s->data = elem;
s->leftchild = CBTree1();
s->rightchild = CBTree1();
}
return s;
}
int FindIs(const char* is, int n, char ch)
{
int pos = -1;
for (int i = 0; i < n; ++i)
{
if (is[i] == ch)
{
pos = i;
break;
}
}
return pos;
}
BtNode* CreatePI(const char* ps, const char* is, int n)
{
BtNode* s = NULL;
if (n > 0)
{
s = BuyNode();
s->data=ps[0];
int pos = FindIs(is, n, ps[0]);
if (pos == -1)exit(1);
s->leftchild = CreatePI(ps+1,is,pos);
s->rightchild = CreatePI(ps+1+pos,is+1+pos,n-pos-1);
}
return s;
}
BtNode* CreateIL(const char* is, const char* ls, int n)
{
BtNode* s = NULL;
if (n > 0)
{
s = BuyNode();
s->data = ls[n-1];
int pos = FindIs(is, n, ls[n-1]);
if (pos == -1)exit(1);
s->leftchild = CreateIL(is, ls, pos);
s->rightchild = CreateIL(is + pos+1, ls+pos, n - pos - 1);
}
return s;
}
//中序和后序构建
BtNode* CreateBinaryTreePI(const char* is, const char* ls, int n)
{
if (is == NULL || ls == NULL || n <= 0) return NULL;
else return CreatePI(is, ls, n);
}
//先序和中序构建
BtNode* CreateBinaryTreeIL(const char* ps, const char* is, int n)
{
if (ps == NULL || is == NULL || n <= 0) return NULL;
else return CreateIL(ps, is, n);
}
int main()
{
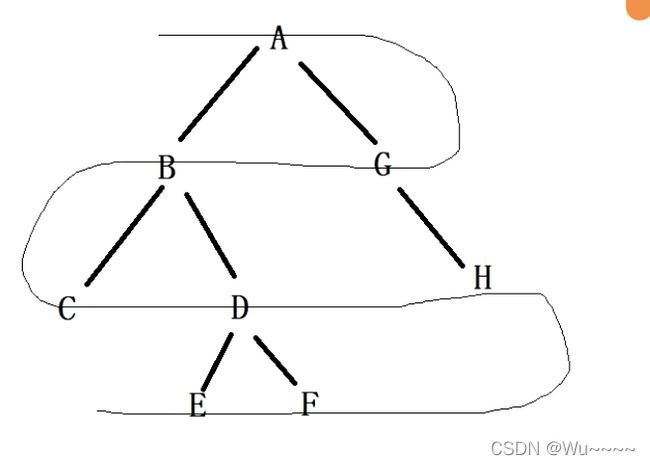
char ps[] = { "ABCDEFGH" };
char is[] = { "CBEDFAGH" };
char ls[] = { "CEFDBHGA" };
int n = strlen(ps);
BinaryTree root = NULL;
root = CreateBinaryTreePI(ps, is, n);
PreOrder(root);
cout << endl;
InOrder(root);
cout << endl;
PastOrder(root);
cout << endl;
return 0;
}
== s->leftchild = CreatePI(ps+1,is,pos);
s->rightchild = CreatePI(ps+1+pos,is+1+pos,n-pos-1);==
== s->leftchild = CreateIL(is, ls, pos);
s->rightchild = CreateIL(is + pos+1, ls+pos, n - pos - 1);==
非递归实现先、中、后序遍历
非递归的中序遍历1:
void NiceInOrder(BtNode* ptr)
{
if (ptr == NULL)return;
std::stack<BtNode*>st;
while (ptr != NULL || !st.empty())
{
while (ptr != NULL)
{
st.push(ptr);
ptr = ptr->leftchild;
}
ptr = st.top(); st.pop();
cout << ptr->data;
ptr = ptr->rightchild;
}
cout << endl;
}
非递归的后序遍历1:
void NicePastOrder(BtNode* ptr)
{
if (ptr == NULL) return;
std::stack<BtNode*> st;
BtNode* tag = NULL;
while (ptr != NULL || !st.empty())
{
while (ptr != NULL)
{
st.push(ptr);
ptr = ptr->leftchild;
}
ptr = st.top(); st.pop();
if (ptr->rightchild == NULL || ptr->rightchild == tag)
{
cout << ptr->data;
tag = ptr;
ptr = NULL; //?
}
else
{
st.push(ptr);
ptr = ptr->rightchild;
}
}
cout << endl;
}
非递归的后序遍历2:
struct StkNode
{
BtNode* pnode;
int pos;
public:
StkNode(BtNode* p) :pnode(p), pos(0) {}
};
void StkNicePastOrder(BtNode* ptr)
{
if (ptr == NULL) return;
stack<StkNode> st;
st.push(StkNode(ptr));
while (!st.empty())
{
StkNode node = st.top(); st.pop();
if (++node.pos == 3)
{
cout << node.pnode->data;
}
else
{
st.push(node);
if (node.pos == 1 && node.pnode->leftchild != NULL)
{
st.push(StkNode(node.pnode->leftchild));
}
else if (node.pos == 2 && node.pnode->rightchild != NULL)
{
st.push(StkNode(node.pnode->rightchild));
}
}
}
cout << endl;
}
非递归的中序遍历2:
void StkNiceInOrder(BtNode* ptr)
{
if (ptr == NULL) return;
stack<StkNode> st;
st.push(StkNode(ptr));
while (!st.empty())
{
StkNode node = st.top(); st.pop();
if (++node.pos == 2)
{
cout << node.pnode->data;
if (node.pnode->rightchild != NULL)
{
st.push(StkNode(node.pnode->rightchild));
}
}
else
{
st.push(node);
if (node.pnode->leftchild != NULL)
{
st.push(StkNode(node.pnode->leftchild));
}
}
}
cout << endl;
}
非递归的先序遍历:
void NicePreOrder(BtNode* ptr)
{
if (ptr == NULL) return;
stack<BtNode*> st;
st.push(ptr);
while (!st.empty())
{
ptr = st.top(); st.pop();
cout << ptr->data;
if (ptr->rightchild != NULL)
{
st.push(ptr->rightchild);
}
if (ptr->leftchild != NULL)
{
st.push(ptr->leftchild);
}
}
cout << endl;
}
层次遍历:
void LevelOrder(BtNode* ptr)
{
if (ptr == NULL) return;
queue<BtNode*> qu;
qu.push(ptr);
while (!qu.empty())
{
ptr = qu.front(); qu.pop();
cout << ptr->data;
if (ptr->leftchild != NULL)
{
qu.push(ptr->leftchild);
}
if (ptr->rightchild != NULL)
{
qu.push(ptr->rightchild);
}
}
cout << endl;
}
Z型层次遍历
void ZLevelOrder(BtNode* ptr)
{
if (ptr == NULL) return;
stack<BtNode*> ast;
stack<BtNode*> bst;
ast.push(ptr);
while (!ast.empty() || !bst.empty())
{
while (!ast.empty())
{
ptr = ast.top(); ast.pop();
cout << ptr->data;
if (ptr->leftchild != NULL)
{
bst.push(ptr->leftchild);
}
if (ptr->rightchild != NULL)
{
bst.push(ptr->rightchild);
}
}
while (!bst.empty())
{
ptr = bst.top(); bst.pop();
cout << ptr->data;
if (ptr->rightchild != NULL)
{
ast.push(ptr->rightchild);
}
if (ptr->leftchild != NULL)
{
ast.push(ptr->leftchild);
}
}
}
}
数组形式存储,实现二叉树的中序遍历
void InOrder(int* tree, int i, int n)
{
if (i < n && tree[i] != -1)
{
InOrder(tree, i * 2 + 1, n); // leftchild;
cout << tree[i] << " ";
InOrder(tree, i * 2 + 2, n); // rightchild
}
}
int main()
{
int tree[] = { 31,23,12,66,-1,5,17,70,62,-1,-1,-1,88,-1,55 };
int n = sizeof(tree) / sizeof(tree[0]);
InOrder(tree, 0, n);
return 0;
}
2.5计算二叉树的结点个数和深度
/二叉树的个数
int Count(BtNode* ptr)
{
if (ptr == NULL) return 0;
else return Count(ptr->leftchild) + Count(ptr->rightchild) + 1;
}
//二叉树的深度
int Depth(BtNode* ptr)
{
if (ptr == NULL) return 0;
else return std::max(Depth(ptr->leftchild), Depth(ptr->rightchild)) + 1;
}
三、二叉树的判定
3.1判断是否为满二叉树
bool Is_FullBinaryTree(BtNode* ptr)
{
bool tag = true;
if (ptr == NULL) return tag;
queue<BtNode*> aqu;
queue<BtNode*> bqu;
int s = 1;
aqu.push(ptr);
while (!aqu.empty() || !bqu.empty())
{
if (s != aqu.size())
{
tag = false;
break;
}
while (!aqu.empty())
{
ptr = aqu.front(); aqu.pop();
if (ptr->leftchild != NULL) bqu.push(ptr->leftchild);
if (ptr->rightchild != NULL) bqu.push(ptr->rightchild);
}
s += s;
if (s != bqu.size())
{
tag = false;
break;
}
while (!bqu.empty())
{
ptr = bqu.front(); bqu.pop();
if (ptr->leftchild != NULL) aqu.push(ptr->leftchild);
if (ptr->rightchild != NULL) aqu.push(ptr->rightchild);
}
s += s;
}
return tag;
}
typedef char ElemType;
typedef struct BtNode
{
ElemType data = '\0';
std::shared_ptr<BtNode> leftchild = nullptr; //BtNode* leftchild;
std::shared_ptr<BtNode> rightchild = nullptr;
};
BtNode* Buynode()
{
BtNode* s = (BtNode*)malloc(sizeof(BtNode));
if (NULL == s)exit(1);
memset(s, 0, sizeof(BtNode));
return s;
}
int FindIs(const char* is, int n, char ch)
{
int pos = -1;
for (int i = 0; i < n; ++i)
{
if (is[i] == ch)
{
pos = i;
break;
}
}
return pos;
}
std::shared_ptr<BtNode> CreatePI(const char* ps, const char* is, int n)
{
std::shared_ptr<BtNode> s(NULL);
if (n >= 1)
{
s = std::make_shared<BtNode>();
s->data = ps[0];
int pos = FindIs(is, n, ps[0]);
if (pos == -1) exit(1);
s->leftchild = CreatePI(ps + 1, is, pos);
s->rightchild = CreatePI(ps + pos + 1, is + pos + 1, n - pos - 1);
}
return s;
}
std::shared_ptr<BtNode> CreateBinartTreePI(const char* ps, const char* is, int n)
{
if (ps == NULL || is == NULL || n <= 0) return NULL;
else return CreatePI(ps, is, n);
}
void InOrder(std::shared_ptr<BtNode>& ptr)
{
if (ptr != NULL)
{
InOrder(ptr->leftchild);
cout << ptr->data << " ";
InOrder(ptr->rightchild);
}
}
int main()
{
char ps[] = { "ABCDEFGH" };
char is[] = { "CBEDFAGH" };
char ls[] = { "CEFDBHGA" };
int n = strlen(ps);
std::shared_ptr<BtNode> root = CreateBinartTreePI(ps, is, n);
InOrder(root);
}
void ClearBinaryTree(BtNode* ptr)
{
if (ptr != NULL)
{
ClearBinaryTree(ptr->leftchild);
ClearBinaryTree(ptr->rightchild);
delete[]ptr;
}
}
3.2是否是完全二叉树
typedef char ElemType;
typedef struct BtNode
{
ElemType data;
struct BtNode* leftchild;
struct BtNode* rightchild;
}BtNode, * BinaryTree;
bool Is_CompBinaryTree(BtNode* ptr)
{
bool tag = true;
if (ptr == NULL) return tag;
queue<BtNode*> qu;
qu.push(ptr);
while (!qu.empty())
{
ptr = qu.front(); qu.pop();
if (NULL == ptr) break;
qu.push(ptr->leftchild);
qu.push(ptr->rightchild);
}
while (!qu.empty())
{
if (qu.front() != NULL)
{
tag = false;
break;
}
qu.pop();
}
}
四、二叉树的查询
4.1在二叉树中查询Value值,如果存在返回结点的地址,否则返回空
typedef int ElemType;
typedef struct BtNode
{
ElemType data;
struct BtNode* leftchild;
struct BtNode* rightchild;
}BtNode, * BinaryTree;
BtNode* FindValue(BtNode* ptr, ElemType val)
{
if (ptr == NULL || ptr->data == val)
{
return ptr;
}
else
{
BtNode* p = FindValue(ptr->leftchild, val);
if (NULL == p)
{
p = FindValue(ptr->rightchild, val);
}
return p;
}
}
4.2给定一个二叉树,找到该树中某个指定节点的双亲
BtNode* FindPa(BtNode* ptr, BtNode* child)
{
if (ptr == NULL || ptr->leftchild == child || ptr->rightchild == child)
{
return ptr;
}
else
{
BtNode* p = FindPa(ptr->leftchild, child);
if (NULL == p)
{
p = FindPa(ptr->rightchild, child);
}
return p;
}
}
BtNode* FindParent(BtNode* ptr, BtNode* child)
{
if (ptr == NULL || child == NULL || ptr == child) return NULL;
else return FindPa(ptr, child);
}