机器学习：详细推导支持向量机SVM原理+Python实现

0 写在前面

机器学习强基计划聚焦深度和广度，加深对机器学习模型的理解与应用。“深”在详细推导算法模型背后的数学原理；“广”在分析多个机器学习模型：决策树、支持向量机、贝叶斯与马尔科夫决策、强化学习等。

详情：机器学习强基计划(附几十种经典模型源码合集)

1 什么是支持向量机？

支持向量机(Support Vector Machine, SVM)是基于训练集在样本空间或其映射空间中寻找一个最鲁棒的划分超平面将不同类别样本划分开的分类方法。

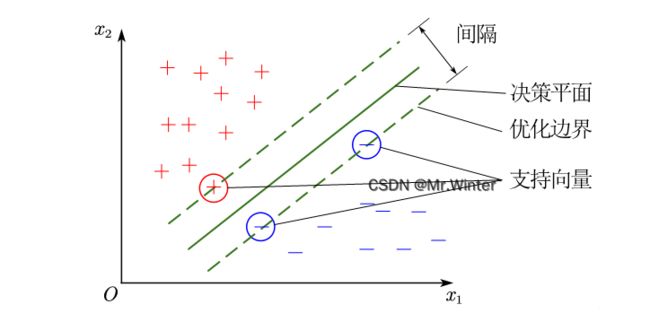
定义两个异类样本集到划分超平面最小距离之和为间隔(margin)，如图所示。直观地，间隔越大则划分对训练样本局部扰动的容忍性越好，泛化能力与鲁棒性越强。间隔并非由所有训练样本决定，而是由距离分类决策超平面最近的少量样本决定，这些样本称为支持向量(Support Vector)。

设划分超平面方程为$\pi :{\mathbf{w}}^T\mathbf{x}+b=0$，根据机器学习强基计划3-1：图文详解超平面、函数间隔、几何间隔可以计算间隔

$$d=2\underset{i}{\min }\frac{\left|{\mathbf{w}}^T{\mathbf{x}}_i+b\right|}{\Vert \mathbf{w}\Vert }=2\underset{i}{\min }\frac{y_i\left({\mathbf{w}}^T{\mathbf{x}}_i+b\right)}{\Vert \mathbf{w}\Vert }$$

即样本到超平面最小几何间隔的两倍——也就是正负支持向量之间的几何间隔，优化目标是最大化间隔${\max }_{\mathbf{w},b}d$

2 支持向量机的优化目标

原始优化目标的形式较为复杂，注意到给定一个超平面，样本的几何间隔随之确定，但函数间隔却具有冗余的尺度自由度，函数间隔的取值并不影响优化问题的解，不妨通过增加约束来降低问题复杂度——令函数间隔${\min }_i\left|{\mathbf{w}}^T{\mathbf{x}}_i+b\right|=1$，优化目标变为

$$\{\begin{array}{l}\underset{\mathbf{w},b}{\max }\frac{2}{\Vert \mathbf{w}\Vert }\iff \underset{\mathbf{w},b}{\min }\frac{1}{2}{\Vert \mathbf{w}\Vert }^2\\ \mathrm{s}.\mathrm{t}.y_i\left({\mathbf{w}}^T{\mathbf{x}}_i+b\right)⩾1\left(i=1,2,\cdots ,m\right)\end{array}$$

所以一句话总结SVM的核心：以函数间隔为约束，最大化几何间隔。

用拉格朗日乘数法化约束优化问题为无约束优化，设拉格朗日函数为

$$L\left(\mathbf{w},b,\mathbf{\alpha }\right)=\frac{1}{2}{\Vert \mathbf{w}\Vert }^2+\sum _{i=1}^m{\alpha }_i\left(1-y_i\left({\mathbf{w}}^T{\mathbf{x}}_i+b\right)\right)$$

则优化目标变为

$$\{\begin{array}{l}\underset{\mathbf{w},b}{\mathrm{argmin}}L\left(\mathbf{w},b,\mathbf{\alpha }\right)\\ \begin{array}{r}{\nabla }_{\mathbf{w}}L\left(\mathbf{w},b,\mathbf{\alpha }\right)=\mathbf{w}-{\sum }_{i=1}^m{\alpha }_i{y}_i{\mathbf{x}}_i=0\\ {\nabla }_{b}L\left(\mathbf{w},b,\mathbf{\alpha }\right)=-{\sum }_{i=1}^m{\alpha }_i{y}_i=0\\ {\alpha }_i⩾0\\ 1-y_i\left({\mathbf{w}}^T{\mathbf{x}}_i+b\right)⩽0\\ {\alpha }_i\left(1-y_i\left({\mathbf{w}}^T{\mathbf{x}}_i+b\right)\right)=0\end{array}\}\left(i=1,2,\cdots ,m\right),KKT\text{约束}\end{array}$$

将${\nabla }_{\mathbf{w}}L\left(\mathbf{w},b,\mathbf{\alpha }\right)$、${\nabla }_{b}L\left(\mathbf{w},b,\mathbf{\alpha }\right)$约束代入$L\left(\mathbf{w},b,\mathbf{\alpha }\right)$消去$\mathbf{w},b$得到原问题的对偶形式

$$\{\begin{array}{l}\underset{\mathbf{\alpha }}{\mathrm{argmax}}\Gamma \left(\mathbf{\alpha }\right)\\ \begin{array}{r}{\alpha }_i⩾0\\ 1-y_i\left({\mathbf{w}}^T{\mathbf{x}}_i+b\right)⩽0\\ {\alpha }_i\left(1-y_i\left({\mathbf{w}}^T{\mathbf{x}}_i+b\right)\right)=0\end{array}\}\left(i=1,2,\cdots ,m\right),KKT\text{约束}\end{array}$$

其中

$$\Gamma \left(\mathbf{\alpha }\right)=\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{\mathbf{x}}_i^T{\mathbf{x}}_j$$

这些公式让人看得头皮发麻，但却是理解SVM底层逻辑不可缺少的。简单解释一下上面在做什么：

• 对偶问题，在凸优化理论中，对偶问题是一种常见的技巧，它可以使原本复杂的问题变简单。在SVM中，原问题需要同时优化$\mathbf{w},b$两个变量，但对偶问题只需要优化$\mathbf{\alpha }$一个变量，问题复杂度显著下降
• 将不等式约束优化问题化为无约束优化问题时会产生KKT(Karush-Kuhn-Tucker)条件，对偶问题计算的最优解一般不如原问题最优解，只有在满足KKT条件时才能保证二者相同

综上所述，上面的复杂推导实际上是为了更好地解决问题。

3 KKT条件计算支持向量

根据KKT条件

• 若${\alpha }_i=0$则该样本无约束作用，处于正确的分类域内
• 若${\alpha }_i>0$则样本满足$1=y_i\left({\mathbf{w}}^T{\mathbf{x}}_i+b\right)$，处于优化边界构成支持向量集$\mathcal{S}$。因此SVM在训练完成后，大部分在间隔外不受约束的训练样本都无需保留，最终模型只与支持向量有关。解得后即得

$$\{\begin{array}{l}\mathbf{w}={\sum }_{i=1}^m{\alpha }_i{y}_i{\mathbf{x}}_i\\ b=\frac{1}{|\mathcal{S}|}{\sum }_{{\mathbf{x}}_i,y_i\in \mathcal{S}}\left(\frac{1}{y_i}-{\mathbf{w}}^T{\mathbf{x}}_i\right)\end{array}$$

4 软间隔策略

前述严格满足$y_i\left({\mathbf{w}}^T{\mathbf{x}}_i+b\right)⩾1\left(i=1,2,\cdots ,m\right)$的策略称为硬间隔(hard margin)，在硬间隔下模型可能会因为噪点的存在产生过拟合(甚至因为异常值无法计算满足硬间隔的超平面)，如图(b)所示

因此允许SVM在部分样本上分类出错但约束误分类的样本尽量少以提高鲁棒性的策略称为软间隔(soft margin)，如图(c)所示

与硬间隔相比，软间隔SVM多引入了松弛变量${\xi }_i⩾0$表征样本不满足硬间隔约束的程度

$$\{\begin{array}{l}\underset{\mathbf{w},b,{\xi }_i}{\min }\frac{1}{2}{\Vert \mathbf{w}\Vert }^2+C{\sum }_{i=1}^m{\xi }_i\\ \mathrm{s}.\mathrm{t}.\{\begin{array}{l}{y}_i\left({\mathbf{w}}^T{\mathbf{x}}_i+b\right)⩾1-{\xi }_i\\ {\xi }_i⩾0\end{array}\left(i=1,2,\cdots ,m\right)\end{array}$$

其中$C$称为惩罚因子，$C$越大软间隔代价越大，误分类样本越少，模型越趋近硬间隔SVM

松弛变量的几何意义如图所示。正确的分类且处于优化边界外的样本${\xi }_i=0$，正确分类但处于优化边界内的样本$0<{\xi }_i<1$，错误分类的样本${\xi }_i⩾1$。

5 Python实现支持向量机

SVM背后实现的SMO算法非常复杂，另开一篇文章详细推导序列最小优化SMO算法+Python实现叙述。本文采用sklearn库模型来体验一下支持向量机。

5.1 构造数据集

使用sklearn.datasets的make_blobs构造二分类数据集，并打印正负样本散点

# 原始数据
X, y = make_blobs(n_samples=80, centers=2, cluster_std=1.2, random_state=6)

# 添加噪声
noise_x = np.array([[5, -5]])
X = np.vstack([X, noise_x])
noise_y = np.array([1])
y = np.hstack([y, noise_y])

data = []
for i in range(len(X)):
    index = np.where(y == i)[0]
    data.append(X[index, :])
plt.scatter(data[0][:, 0], data[0][:, 1], marker='o', s=40, cmap=plt.cm.Paired)
plt.scatter(data[1][:, 0], data[1][:, 1], marker='s', s=40, cmap=plt.cm.Paired)

5.2 构造软硬间隔SVM

硬间隔支持向量机

clf = svm.SVC(kernel='linear', C=1000)
clf.fit(X, y)
Z4 = clf.decision_function(xy).reshape(XX.shape)
plt.contour(XX, YY, Z4, colors='black', levels=[-1, 0, 1], alpha=0.8, linestyles=['--', '-', '--'])
plt.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], s=140,
            linewidth=1, facecolors='none', edgecolors='k')

软间隔支持向量机

clf = svm.SVC(kernel='linear', C=1)
clf.fit(X, y)
Z4 = clf.decision_function(xy).reshape(XX.shape)
plt.contour(XX, YY, Z4, colors='black', levels=[-1, 0, 1], alpha=0.8, linestyles=['--', '-', '--'])
plt.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], s=140,
            linewidth=1, facecolors='none', edgecolors='k')

可以看到区别仅仅在于惩罚因子的大小

5.3 可视化

上面代码运行后得到如下的结果

---

更多精彩专栏：

• 《ROS从入门到精通》
• 《机器人原理与技术》
• 《机器学习强基计划》
• 《计算机视觉教程》
• …

源码获取 · 技术交流 · 抱团学习 · 咨询分享 请联系