机器学习基础|多项式朴素贝叶斯算法及实战
文章目录
-
- 朴素贝叶斯
-
- 朴素贝叶斯的概念
- 概率的计算
- 朴素贝叶斯的种类
- 多项式朴素贝叶斯
- Sklearn朴素贝叶斯API
- 朴素贝叶斯实战案例
-
- 问题背景
- 解题流程
- 完整代码
- 总结
朴素贝叶斯
朴素贝叶斯的概念
朴素贝叶斯法是一种基于贝叶斯定理与特征条件独立假设的分类方法。其中朴素指的就是条件独立 。
朴素贝叶斯在分类的时候不是直接返回分类,而是返回属于某个分类的概率。
例如对文章的类别进行判断:
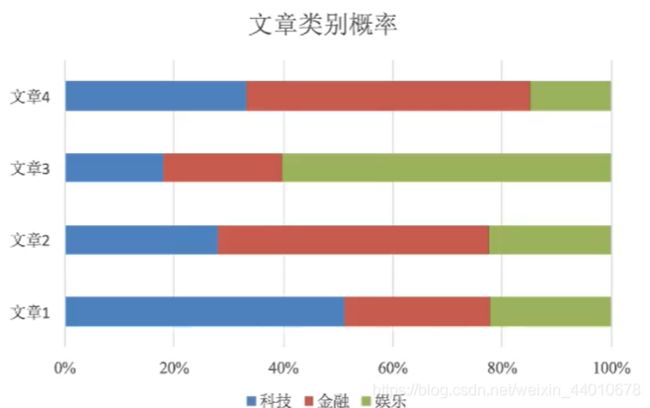
计算出的是每篇文章属于某个类别的概率,哪个类别占的比例比较大,则将文章归为哪一类。简单地说,朴素贝叶斯是根据概率的大小进行分类。
概率的计算
朴素贝叶斯需要用到一些概率知识,即联合概率和条件概率。
联合概率:包含多个条件,且所有条件同时成立的概率。
P(A,B)=P(A)P(B)
条件概率:事件A在另一个时间B已经发生条件下的概率。
P(A1,A2|B)=P(A1|B)P(A2|B)
但是需要注意上述的求概率公式只适用于各个特征之间是条件独立(每个特征之间没有必然关系)的。
朴素贝叶斯的种类
在sklearn中提供了三种不同类型的贝叶斯模型算法
- 高斯朴素贝叶斯
- 多项式朴素贝叶斯
- 伯努利朴素贝叶斯
多项式朴素贝叶斯
多项式朴素贝叶斯主要适用于离散特征的概率计算,且sklearn的多项式模型不接受输入负值。 若处理连续性变量要选择高斯模型。多项式朴素贝叶斯多用于文档分类,它可以计算出一篇文档为某些类别的概率,最大概率的类型就是该文档的类别。举个例子,比如判断一个文档属于体育类别还是财经类别,那么只需要判断P(体育|文档)和P(财经|文档)的大小。而文档中其实就是一个个关键词(提取出的文档关键词),所以我们需要计算的P(体育|词1,词2,词3......)和P(财经|词1,词2,词3.....)。我们之前求得都是一个条件下多类别的公式,例如P(A1,A2|B)=P(A1|B)P(A2|B)。而我们现在求的是多个条件一个类别,那么该如何求呢?这就需要用到朴素贝叶斯公式
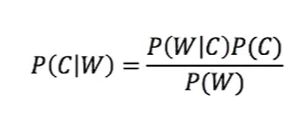
其中F1,F2为文档中的关键词。
所以可得
P(体育|词1,词2,词3)=P(词1,词2,词3|体育)*P(体育)/P(词1,词2,词3)
P(财经|词1,词2,词3)=P(词1,词2,词3|财经)*P(财经)/P(词1,词2,词3)
上式中因为分母都有P(词1,词2,词3),故可以消去。只需要比较P(词1,词2,词3|体育)*P(体育)和P(词1,词2,词3|财经)*P(财经)即可。
其中
P( C):每个文档类别的概率(某个文档类别文章的数量/总文档数量)
P(F1,F2,F3|C):给定类别下特征的概率,此处的特征就是预测文档中出现的词语
- P(F1|C)=Ni/N:F1为预测文档中的某一个词,C为指定的类别
- Ni:F1这个词在C类别所有文档中出现的次数
- N:所属类别C下的文档所有词出现的次数和
举个例子:
下图中的训练集中一共有30篇科技文章,60篇娱乐文章,共计90篇文章。这些文章中根据tf-idf提取出重要的词语分别有商场、影院、支付宝和云计算,并统计了在不同类别文章中出现的次数。
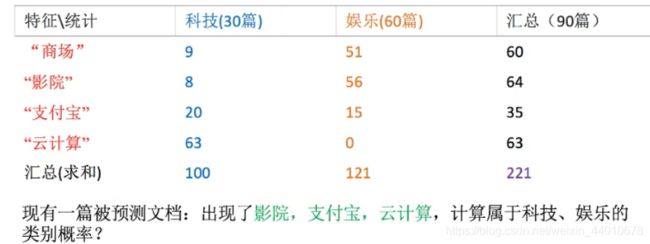
现在有一个将要被预测的文章,该文章中出现重要的词为影院,支付宝和云计算,则计算该文章属于科技、娱乐的概率分别是多少?
那么我们可以直接带入式子中进行计算。
P(科技|影院,支付宝,云计算)=P(影院,支付宝,云计算|科技)*P(科技)=(8/100)(20/100)(63/100)(30/90)=0.005
P(娱乐|影院,支付宝,云计算)=P(影院,支付宝,云计算|娱乐)*P(娱乐)=(56/121)(15/121)(0/121)(60/90)=0
我们发现预测文章属于娱乐的概率为0,合适吗?
肯定不合适,不能因为一个词不出现而否定了其他关键词。那么如何解决呢?
需要引入拉普拉斯平滑系数
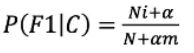
![]()
那么原来的式子就变成了
P(科技|影院,支付宝,云计算)=P(影院,支付宝,云计算|科技)*P(科技)=((1+8)/(100+1*4))((1+20)/(100+1*4))((1+63)/(100+1*4))(30/90)=
P(娱乐|影院,支付宝,云计算)=P(影院,支付宝,云计算|娱乐)*P(娱乐)=((1+56)/(121+1*4))((1+15)/(121+1*4))((1+0)/(121+1*4))(60/90)
这样就不会出现等于0的情况了。
Sklearn朴素贝叶斯API
MultinomialNB(alpha=1.0, fit_prior=True, class_prior=None)
#alpha:拉普拉斯平滑系数,默认为1.0。注意拉普拉斯平滑系数不是超参数,并不会影响最后的结果。
朴素贝叶斯实战案例
问题背景
使用sklearn自带的数据集。使用fetch_20newsgroups中的数据,包含了20个主题的18000个新闻组的帖子,利用多项式朴素贝叶斯进行分类。
解题流程
1、导入20类新闻数据
from sklearn.datasets import fetch_20newsgroups
news = fetch_20newsgroups(subset='all')
type(news)
sklearn.utils.Bunch
sklearn.utils.Bunch本质上的数据类型是dict,有以下属性:
- DESCR:数据描述。
- target_names:标签名。可自定义,默认为文件夹名。
- filenames:文件名。
- target:文件分类。如猫狗两类的话,与filenames一一对应为0或1。
- data:数据数组。
我们可以查看一下data和target
news.data
news.target
from sklearn.model_selection import train_test_split
#进行训练集和测试集切分
x_train, x_test, y_train, y_test = train_test_split(news.data,news.target,test_size=0.25)
3、特征的提取
from sklearn.feature_extraction.text import TfidfVectorizer
#对数据集进行提取
tf = TfidfVectorizer()
x_train = tf.fit_transform(x_train)
x_test = tf.transform(x_test)
print(tf.get_feature_names())
from sklearn.naive_bayes import MultinomialNB
mlt = MultinomialNB(alpha=1.0)
mlt.fit(x_train,y_train)
y_predict = mlt.predict(x_test)
print(x_train.toarray())#默认为sparse形式,转化为array形式
print("预测的文章类别为:",y_predict)
#得出准确率
print("准确率为:",mlt.score(x_test,y_test))
准确率为: 0.8518675721561969
6、召回率的计算
from sklearn.metrics import classification_report
print("每个类别的精确率和召回率:",classification_report(y_test,y_predict,target_names=news.target_names))
完整代码
from sklearn.datasets import fetch_20newsgroups#自带数据集
from sklearn.model_selection import train_test_split#切分测试集
from sklearn.feature_extraction.text import TfidfVectorizer#tf-idf
from sklearn.naive_bayes import MultinomialNB#贝叶斯
from sklearn.metrics import classification_report#召回率
news = fetch_20newsgroups(subset='all')
#进行训练集和测试集切分
x_train, x_test, y_train, y_test = train_test_split(news.data,news.target,test_size=0.25)
#对数据集进行提取
tf = TfidfVectorizer()
x_train = tf.fit_transform(x_train)
x_test = tf.transform(x_test)
#print(tf.get_feature_names())
mlt = MultinomialNB(alpha=1.0)
mlt.fit(x_train,y_train)
y_predict = mlt.predict(x_test)
#print(x_train.toarray())#默认为sparse形式,转化为array形式
#得出准确率
print("准确率为:",mlt.score(x_test,y_test))
#得出召回率
print("每个类别的精确率和召回率:",classification_report(y_test,y_predict,target_names=news.target_names))
那么准确率能不能提高呢,其实不好提高,因为朴素贝叶斯中没有超参数,不需要调参。所以训练集就决定了结果的好坏。
总结
朴素贝叶斯的优点:
- 朴素贝叶斯模型发源于古典数学理论,有稳定的分类效率。
- 对缺失数据不太敏感,算法也比较简单,常用于文本分类。
- 分类准确度高,速度快。
朴素贝叶斯的缺点:
- 由于使用了样本属性独立性的假设,所以如果样本属性有关联时其效果不好




