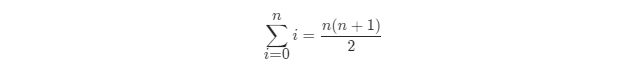循环排序（Cyclic Sort）

Pattern: Cyclic Sort，循环排序

介绍部分来自：https://www.zhihu.com/question/36738189/answer/908664455 作者：穷码农

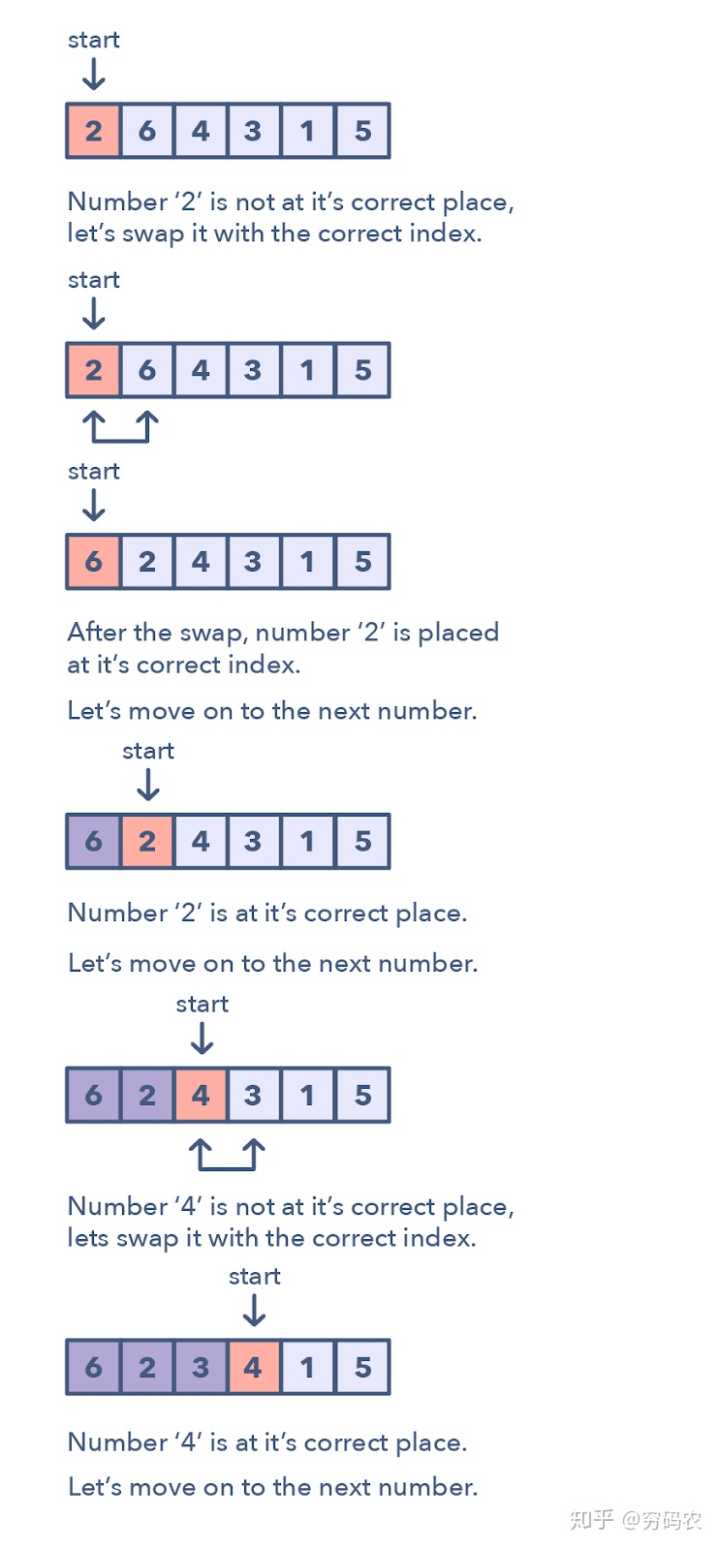
这种模式讲述的是一直很好玩的方法：可以用来处理数组中的数值限定在一定的区间的问题。这种模式一个个遍历数组中的元素，如果当前这个数它不在其应该在的位置的话，咱们就把它和它应该在的那个位置上的数交换一下。你可以尝试将该数放到其正确的位置上，但这复杂度就会是O(n^2)。这样的话，可能就不是最优解了。因此循环排序的优势就体现出来了。

咋鉴别这种模式？

• 这些问题一般设计到排序好的数组，而且数值一般满足于一定的区间
• 如果问题让你需要在排好序/翻转过的数组中，寻找丢失的/重复的/最小的元素

总结: 关键是要理解和应用 数组值与下标 之间存在的关系。

经典题目：

1、Cyclic Sort (easy)

​ Cyclic Sort

2、Find the Missing Number (easy)

268. 丢失的数字

描述：

​ 给定一个包含 [0, n] 中 n 个数的数组 nums ，找出 [0, n] 这个范围内没有出现在数组中的那个数。

​ 进阶：

​ 你能否实现线性时间复杂度、仅使用额外常数空间的算法解决此问题?

示例：

示例 1：

输入：nums = [3,0,1]
输出：2
解释：n = 3，因为有 3 个数字，所以所有的数字都在范围 [0,3] 内。2 是丢失的数字，因为它没有出现在 nums 中。

示例 2：

输入：nums = [0,1]
输出：2
解释：n = 2，因为有 2 个数字，所以所有的数字都在范围 [0,2] 内。2 是丢失的数字，因为它没有出现在 nums 中。

示例 3：

输入：nums = [9,6,4,2,3,5,7,0,1]
输出：8
解释：n = 9，因为有 9 个数字，所以所有的数字都在范围 [0,9] 内。8 是丢失的数字，因为它没有出现在 nums 中。

示例 4：

输入：nums = [0]
输出：1
解释：n = 1，因为有 1 个数字，所以所有的数字都在范围 [0,1] 内。1 是丢失的数字，因为它没有出现在 nums 中。

提示：

n == nums.length
1 <= n <= 104
0 <= nums[i] <= n
nums 中的所有数字都 独一无二

可以看官方的解答：https://leetcode-cn.com/problems/missing-number/solution/que-shi-shu-zi-by-leetcode/

异或运算^(两位相等为0，不相等为1)可以进行抵消，例如

• 0^4=4

    0000 = 0
  ^ 0100 = 4 
  ------------
    0100 = 4			

• 4^4=0

    0100 = 4
  ^ 0100 = 4
  -----------
    0000 = 0

将结果的初始值设为 n，再对数组中的每一个数以及它的下标进行一个异或运算，没有抵消掉的数就是缺失的数字：

class Solution {
    public int missingNumber(int[] nums) {
        if (nums.length == 0)
            return 0;
        int res = nums.length;
        for (int i = 0; i < nums.length; i++) {
            res ^= nums[i];
            res ^= i;
        }
        return res;
    }
}

可以用 高斯求和公式 求出 [0…n][0…n] 的和，减去数组中所有数的和，就得到了缺失的数字。高斯求和公式即

class Solution {
    public int missingNumber(int[] nums) {
        if (nums.length == 0)
            return 0;

        int sum = 0;
        for (int i = 1; i <= nums.length; i++) {
            sum += i;
            sum -= nums[i-1];
        }
        
        return sum;
    }
}

3、Find all Missing Numbers (easy)

448. 找到所有数组中消失的数字

描述：

​ 给定一个范围在 1 ≤ a[i] ≤ n ( n = 数组大小 ) 的 整型数组，数组中的元素一些出现了两次，另一些只出现一次。

​ 找到所有在 [1, n] 范围之间没有出现在数组中的数字。

​ 您能在不使用额外空间且时间复杂度为O(n)的情况下完成这个任务吗? 你可以假定返回的数组不算在额外空间内。

示例:

输入:
[4,3,2,7,8,2,3,1]

输出:
[5,6]

看官方解题吧，淦

做完下面的第 4 题后，突然理解。

1 ≤ a[i] ≤ n。可以从 0 开始遍历。将下标为 nums[0...i]-1 的数组的值置为负数。

当走完一遍后，那些没有出现的数字的对应的下标为 nums[i]-1 的值一定为正数。

例如上例中 nums[i] = 5 不存在，所以下标为 nums[i] - 1 即 5-1 = 4 的数即 nums[4] = 8 一定为正数，由此可知道消失的数。

class Solution {
    public List<Integer> findDisappearedNumbers(int[] nums) {
        List<Integer> res = new ArrayList<>();      // 结果

        //  1 ≤ a[i] ≤ n, 将下标为 nums[i]-1 的数全部置为负数
        for (int i = 0; i < nums.length; i++) {
            int index = Math.abs(nums[i]) - 1;      // 重复数字会将 nums[i] 置为负数过了，所以要取绝对值
            if (nums[index] > 0)                    // 大于 0 的数全部置为负数
                nums[index] = -nums[index];
        }
        
        // 找出 正数下标 + 1的值，即为消失的的数字
        for (int i = 0; i < nums.length; i++) {
            if (nums[i] > 0)
                res.add(i + 1);
        }
        
        return res;
    }
}

4、Find the Duplicate Number (easy)

287. 寻找重复数

描述：

​ 给定一个包含 n + 1 个整数的数组 nums，其数字都在 1 到 n 之间（包括 1 和 n），可知至少存在一个重复的整数。假设只有一个重复的整数，找出这个重复的数。

示例：

示例 1:

输入: [1,3,4,2,2]
输出: 2

示例 2:

输入: [3,1,3,4,2]
输出: 3

说明：

​ 不能更改原数组（假设数组是只读的）。
​ 只能使用额外的 O(1) 的空间。
​ 时间复杂度小于 O(n2) 。
​ 数组中只有一个重复的数字，但它可能不止重复出现一次。

详细可参考：双指针

​ 建立数组下标 i 和数值 nums[i] 的映射函数 f(i)。

​ 数组[1,2,4,2,3] ,其映射关系 i -> f(i) 为：

0->1
1->2
2->4
3->2
4->3

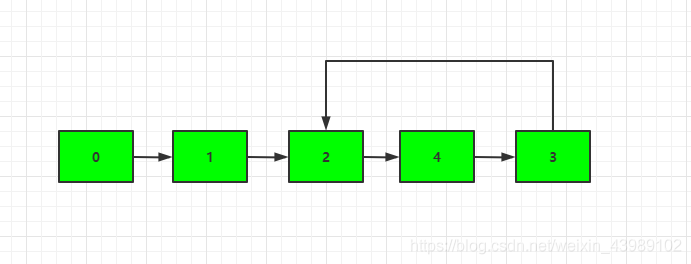
从下标 0 出发，根据 f(i) 计算出一个值，以这个值为新的下标，再计算函数值，如此重复。可得到：

0->1->2->4->3->2->4->3->2->4.....

这样一来，就可以用到之前的理论了。快慢指针类型 中的第 2 题：判断链表是否有环并且返回环入口点。也就是找到相遇点后，再用一个指针从起点和慢指针一起走，他们最终在环入口点相遇。

class Solution {
    public int findDuplicate(int[] nums) {
        int slow = 0;       // 慢指针，做一次映射
        int fast = 0;       // 快指针，做两次映射

        // 至少存在一个重复的整数，所以一定有环。找到相遇点
        do {
            slow = nums[slow];
            fast = nums[nums[fast]];
        }while (slow != fast);

        // 找出环入口点。
        int head = 0;
        while (slow != head){
            head = nums[head];
            slow = nums[slow];
        }

        return head;
    }
}

5、Find all Duplicate Numbers (easy)

442. 数组中重复的数据

描述：

​ 给定一个整数数组 a，其中1 ≤ a[i] ≤ n （n为数组长度）, 其中有些元素出现两次而其他元素出现一次。

​ 找到所有出现两次的元素。

​ 你可以不用到任何额外空间并在O(n)时间复杂度内解决这个问题吗？

示例：

输入:
[4,3,2,7,8,2,3,1]

输出:
[2,3]

由题目 1 ≤ a[i] ≤ n ,可以从0开始遍历，逐一将下标为 nums[0...i]-1 上的值置为负数。

如果有下标为 nums[i]-1 的值已经为负数，则重复出现了。即num[i] = nums[i+n]。

class Solution {
    public List<Integer> findDuplicates(int[] nums) {
        List<Integer> res = new ArrayList<>();  // 结果
        int index = 0;  // 置换的数组下标: num[i] - 1
        for (int i = 0; i < nums.length; i++) {
            index = Math.abs(nums[i]) - 1;  // 置换的下标
            if (nums[index] < 0){           // 该下标的值前面已经置换过了，则为重复出现
                res.add(index + 1);         // index + 1 即为该数
            }
            nums[index] = -nums[index];     // 置换为负数
        }

        return res;
    }
}