备战数学建模15-灰色关联分析与灰色预测模型
目录
一、灰色系统理论与灰色关联分析
1-灰色预测的概念
2-灰色关联度与优势分析
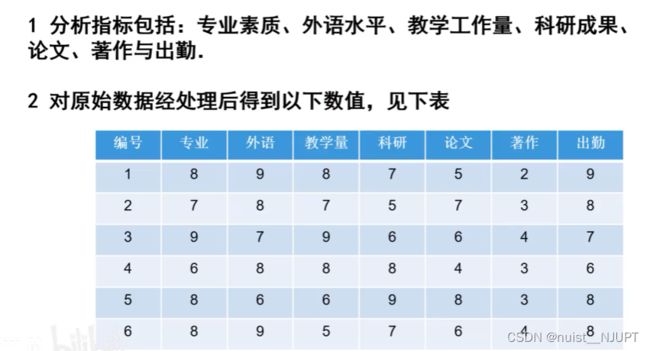
3-灰色关联分析案例分析
4-灰色生成数列
二、灰色预测模型
1-灰色模型GM
2-灰色模型GM的建模步骤
3-灰色预测经典案例1
4-灰色预测模型经典案例2
一、灰色系统理论与灰色关联分析
1-灰色预测的概念
灰色系统的起源及简单介绍如下所示：
灰色系统主要应用于如下四个方面，具体如下：
我们进一步看一下灰色系统的相关概念，具体如下：
我们继续学习一下，什么是灰色预测法 ，具体如下：
灰色预测的常见四种类型如下：
即灰色时间序列预测，畸变预测，系统预测，拓扑预测
2-灰色关联度与优势分析
下面看一下灰色关联度分析的基本步骤，具体如下：
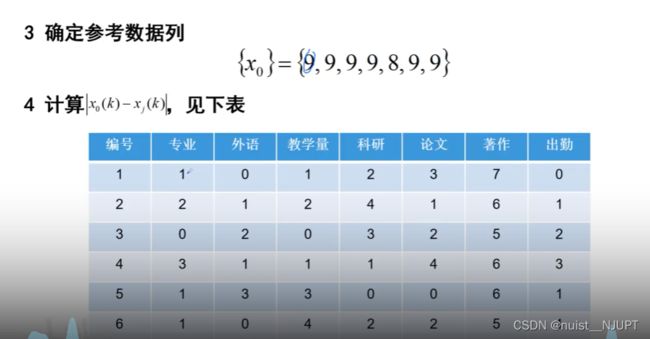
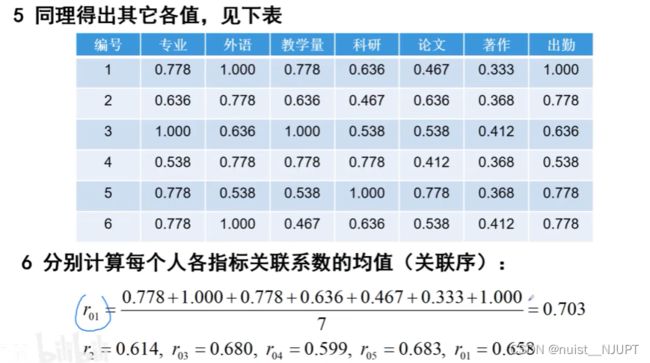
3-灰色关联分析案例分析
有下面的结果r可以发现，编号为1的老师整体评价最高的，编号3和编号5的老师评价相差很近，编号4的老师评价最差。
上述灰色关联分析MATLAB代码如下：
clear; clc
x1 = [8, 9, 8, 7, 5, 2, 9;
7, 8, 7, 5, 7, 3, 8;
9, 7, 9, 6, 6, 4, 7;
6, 8, 8, 8, 4, 3, 6;
8, 6, 6, 9, 8, 3, 8;
8, 9, 5, 7, 6, 4, 8] ;
[n,m] = size(x1) ;
x0 = [9,9,9,9,8,9,9] ;
%数据处理
for i = 1 : n
for j = 1 : m
x(i,j) = abs(x1(i,j) - x0(1,j)) ;
end
end
%计算灰色关联度系数
max = x(1,1) ;
min = x(1,1) ;
for i = 1 : n
for j = 1 : m
if x(i,j)>=max
max=x(i,j) ;
end
end
end
for i = 1 : n
for j = 1 : m
if x(i,j)<=min
min=x(i,j) ;
end
end
end
k=0.5; %分辨系数取值
l=(min+k*max)./(x+k*max);%求关联系数矩阵
disp('关联系数矩阵如下所示：') ;
disp(l) ;
%计算灰色加权关联度，此处默认各个指标的权重一样，直接求均值了
g = sum(l,2) / m ;
[rs,rind]=sort(g,'descend'); %对关联度进行排序
disp('加权关联度如下：') ;
disp(rs) ;
disp('关联度排名如下：') ;
disp(rind) ;
运行结果如下：
总结一下：
灰色关联分析：
【1】确定比较对象（评价对象）(就是数据，并且需要进行规范化处理，就是标准化处理)和参考数列（评价标准，一般该列数列都是1，就是最优的的情况）
【2】确定各个指标权重，可用层次分析确定
【3】计算灰色关联系数
【4】计算灰色加权关联度
【5】评价分析
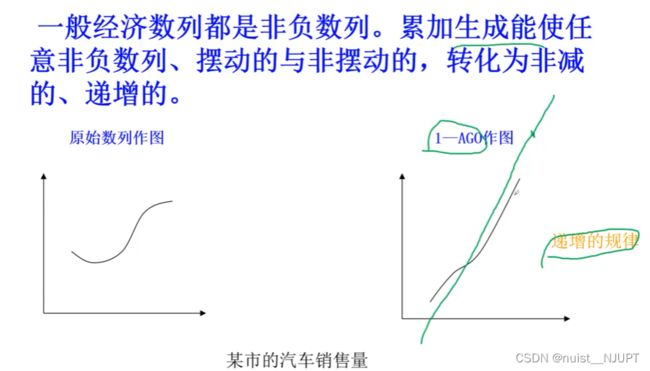
4-灰色生成数列
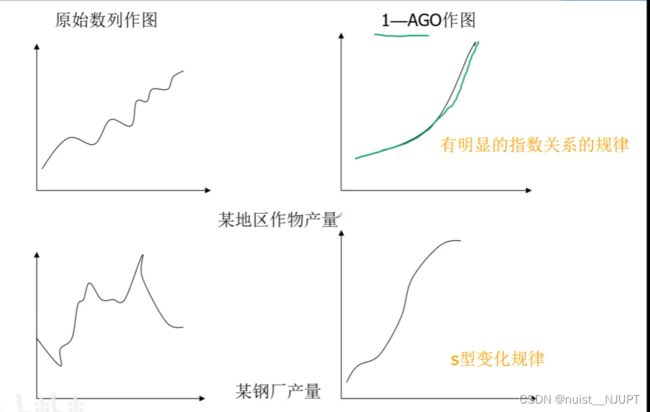
数据生成的意义在于：将数据变成有规律的数列，可以发现其中的规律。
我们看一下累加生成的一般特点，通过累加函数后得到规律性的函数，通过拟合进行预测，具体如下：
二、灰色预测模型
1-灰色模型GM
2-灰色模型GM的建模步骤
灰色预测的前提是必须是通过级别检验，直接用很可能出错。
3-灰色预测经典案例1
如果级别检验不通过，需要累加了一个数，后面再减掉。
注意：这个残差数据有误，具体看代码给出的结果数据。
灰度预测和误差检验MATLAB代码如下所示:
clear; clc
x0 = [71.1, 72.4, 72.4, 72.1, 71.4, 72.0, 71.6] ;
x0 = x0' ;
n = length(x0) ; %数据的维度，n=7
x1 = cumsum(x0) ;
flag = 1 ;
%第一步：级比检验
for k = 2 : n
lamda(k) = x0(k-1) / x0(k) ;
if (lamda(k) < exp(-2 / (n+1)) || lamda(k) > exp(2 / (n+1)))
disp('不通过级比检验！！！') ;
flag = 0 ;
end
end
%第2步：建模并求解
if flag == 1
disp('通过级比检验！！！') ;
alpha = 0.5 ;
z1 = alpha * x1(2:n) + (1 - alpha) * x1(1:n-1) ; %求邻域生成数
Y = x0(2:n) ;
B = [-z1, ones(n-1, 1)] ;
ab = B \ Y ; %求出a，b
disp('a和b的值分别为：') ;
disp(ab(1));
disp(ab(2));
for k = 1 : n
r1(k) = (x0(1) - ab(2) / ab(1)) * exp(-ab(1)*k) + ab(2) / ab(1) ;
if k == 1
r0(k) = x0(k);
else
r0(k) = r1(k) - r1(k-1) ;
end
end
disp('预测的结果如下：') ;
disp(r0) ;
%第3步：模型的2种检验方式
%残差检验
for k = 1 : n
c(k) = (x0(k) - r0(k)) / x0(k);
if k > 1
rou(k) = 1 - (((1-0.5*ab(1)) / (1+0.5*ab(1))) * lamda(k)) ;
end
end
disp('残差如下：') ;
disp(c) ;
%级比偏差检验
disp('级比检验值如下：') ;
disp(rou) ;
end
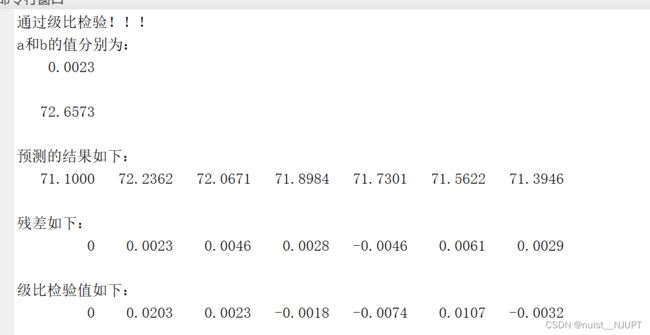
运行结果如下所示：
4-灰色预测模型经典案例2
预测SARS疫情对某些经济指标的影响，准确的说是预测没发生疫情的指标与已经发生疫情的实际指标进行对比，可以得到疫情对经济指标的影响情况。
可以根据月度预测，直接得到每个月的；也可以根据月度总和，即年度预测，根据占比，推出每个月的值。
根据商品的零售预测结果，会发现疫情对商品的零售额影响不大。
模型的结果分析
对商品零售，接待海外旅游，综合服务的灰度预测MATLAB代码如下所示：
未发生疫情的情况下，2003年商品零售额预测代码：
clear; clc
han1 = [83.0, 79.8, 78.1, 85.1, 86.6, 88.2, 90.3, 86.7, 93.3, 92.5, 90.9, 96.9;
101.7, 85.1, 87.8, 91.6, 93.4, 94.5, 97.4, 99.5, 104.2, 102.3, 101, 123.5;
92.2, 114, 93.3, 101, 103.5, 105.2, 109.5, 109.2, 109.6, 111.2, 121.7, 131.3;
105, 125.7, 106.6, 116, 117.6, 118, 121.7, 118.7, 120.2, 127.8, 121.8, 121.9;
139.3, 129.5, 122.5, 124.5, 135.7, 130.8, 138.7, 133.7, 136.8, 138.9, 129.6, 133.7;
137.5, 135.3, 133, 133.4, 142.8, 141.6, 142.9, 147.3, 159.6, 162.1, 153.5, 155.9;
163.2, 159.7, 158.4, 145.2, 124, 144.1, 157, 162.6, 171.8, 180.7, 173.5, 176.5] ;
han = han1(7,:) ;
flag = 1 ;
han1(end,:) = [] ; %最后一行不用，也就是2003年的不用
m = size(han1,2) ; %计算列数，即12个月份
x0 = mean(han1, 2) ; %求每一行12个月的均值
n = length(x0) ; %数据的维度，n=6，也就是6年
for k = 2 : n
lamda(k) = x0(k-1) / x0(k) ;
if (lamda(k) < exp(-2 / (n+1)) || lamda(k) > exp(2 / (n+1)))
disp('不通过级比检验！！！') ;
flag = 0 ;
end
end
if flag == 1
disp('通过级比检验！！！') ;
x1 = cumsum(x0) ; %做一次累加
alpha = 0.4 ;
z1 = alpha * x1(2:n) + (1 - alpha) * x1(1:n-1) ; %求邻域生成数
Y = x0(2:n) ;
B = [-z1, ones(n-1, 1)] ;
ab = B \ Y ; %求出a，b
k = 6 ;
x7hat = (x0(1) - ab(2) / ab(1)) * (exp(-ab(1)*k) - exp(-ab(1)*(k-1))) ; %预测结果的均值
z = m * x7hat ; %总的预测结果
u = sum(han1) / sum(sum(han1)) ;
v = z * u ; %最终的预测结果
disp('未发生SARS疫情的2003年12个月商品零售额预测结果：') ;
disp(v) ;
disp('发生SARS疫情的2003年12个月商品零售额实际情况：') ;
disp(han) ;
end
%级比偏差值检验
flag1 = 1 ;
for k = 2 : n
rou(k) = 1 - (((1-0.5*ab(1)) / (1+0.5*ab(1))) * lamda(k)) ;
end
disp('级比检验结果：') ;
disp(rou) ;
运行结果如下所示：
未发生疫情的情况下，2003年接待海外旅游人数预测MATLAB代码：
clear; clc
han1 = [9.4, 11.3, 16.8, 19.8, 20.3, 18.8, 20.9, 24.9, 24.7, 24.3, 19.4, 18.6;
9.6, 11.7, 15.8, 19.9, 19.5, 17.8, 17.8, 23.3, 21.4, 24.5, 20.1, 15.9;
10.1, 12.9, 17.7, 21, 21, 20.4, 21.9, 25.8, 29.3, 29.8, 23.6, 16.5;
11.4, 26, 19.6, 25.9, 27.6, 24.3, 23, 27.8, 27.3, 28.5, 32.8, 18.5;
11.5, 26.4, 20.4, 26.1, 28.9, 28, 25.2, 30.8, 28.7, 28.1, 22.2, 20.7;
13.7, 29.7, 23.1, 28.9, 29, 27.4, 26, 32.2, 31.4, 32.6, 29.2, 22.9;
15.4, 17.1, 23.5, 11.6, 1.78, 2.61, 8.8, 16.2, 20.1, 24.9, 26.5, 21.8] ;
han = han1(7,:) ;
flag = 1 ;
han1(end,:) = [] ; %最后一行不用，也就是2003年的不用
m = size(han1,2) ; %计算列数，即12个月份
x0 = mean(han1, 2) ; %求每一行12个月的均值
n = length(x0) ; %数据的维度，n=6，也就是6年
for k = 2 : n
lamda(k) = x0(k-1) / x0(k) ;
if (lamda(k) < exp(-2 / (n+1)) || lamda(k) > exp(2 / (n+1)))
disp('不通过级比检验！！！') ;
flag = 0 ;
end
end
if flag == 1
disp('通过级比检验！！！') ;
x1 = cumsum(x0) ; %做一次累加
alpha = 0.5 ;
z1 = alpha * x1(2:n) + (1 - alpha) * x1(1:n-1) ; %求邻域生成数
Y = x0(2:n) ;
B = [-z1, ones(n-1, 1)] ;
ab = B \ Y ; %求出a，b
k = 6 ;
x7hat = (x0(1) - ab(2) / ab(1)) * (exp(-ab(1)*k) - exp(-ab(1)*(k-1))) ; %预测结果的均值
z = m * x7hat ; %总的预测结果
u = sum(han1) / sum(sum(han1)) ;
v = z * u ; %最终的预测结果
disp('未发生SARS疫情的2003年12个月旅游人数预测结果：') ;
disp(v) ;
disp('发生SARS疫情的2003年12个月旅游人数实际情况：') ;
disp(han) ;
end
%级比偏差值检验
flag1 = 1 ;
for k = 2 : n
rou(k) = 1 - (((1-0.5*ab(1)) / (1+0.5*ab(1))) * lamda(k)) ;
end
disp('级比检验结果：') ;
disp(rou) ;
运行结果如下：
未发生疫情的情况下，2003年综合服务业类及情况MATLAB代码，与上面的一样，只需要将数据录入就可以，不再赘述。
总结一下：
灰色预测模型：
【1】数据检验与处理
【2】GM模型建立与求解
【3】残差检验和级比偏差检验