SVM支持向量机之证明SVM (三)
转载:
https://blog.csdn.net/ajianyingxiaoqinghan/article/details/73087304
https://blog.csdn.net/v_july_v/article/details/7624837
本文为个人学习所记,详情请移驾转载出处。
1、线性学习器
感知机算法
感知机算法是1956年提出的,年代久远,依然影响着当今,当然,可以肯定的是,此算法亦非最优,后续会有更详尽阐述。
不过有一点必须清楚,这个算法的作用很简单:不断的训练试错,以期寻找一个合适的超平面。
感知机算法的伪代码如下所示:
给定线性可分的数据集S和学习率η∈R+;
w0←0;b0←0;k←0
R←max i≤i≤l ∥xi∥
重复:
for i=1 to l
if yi[(wk⋅xi)+bk]≤0
then
wk+1 ← wk+ηyixi
bk+1 ← bk+ηyiR2
k ← k+1
end if
end for
直到在for循环中没有错误发生
返回(wk,bk),这里k是错误次数
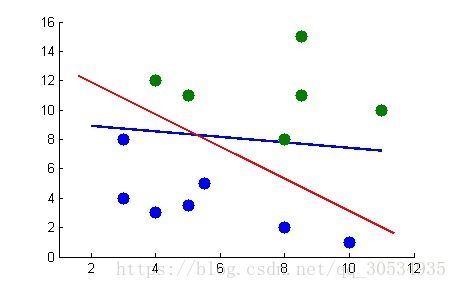
下面举个例子:
如上图1所示,凭我们的直觉可以看出,图中的红线是最优超平面,蓝线则是根据感知机算法在不断的训练中,最终,若蓝线能通过不断的训练移动到红线位置上,则代表训练成功。
既然需要通过不断的训练以让蓝线最终成为最优分类超平面,那么,到底需要训练多少次呢?这个问题可以用Novikoff定理解释。
Novikoff定理:如果分类超平面存在, 仅需在序列S上迭代几次,在界为(2Rγ)2的错误次数下就可以找到分类超平面,算法停止。
- R=max 1≤i≤l ∥xi∥
- γ :扩充间隔(即前文第一章中提到的最大分类间隔;根据误分次数公式可知,迭代次数与对应于扩充(包括偏置)权重的训练集的间隔有关)
Novikoff定理告诉我们当间隔是正的时候感知机算法会在有限次数的迭代中收敛,也就是说Novikoff定理证明了感知机算法的收敛性,即能得到一个界,不至于无穷循环下去。
2、非线性学习器
Mercer定理
Mercer定理:如果函数K是Rn×Rn→R上的映射(也就是从两个n维向量映射到实数域)。
那么如果K是一个有效核函数(也称为Mercer核函数),那么当且仅当对于训练样例{x1,x2,…,xm},其相应的核函数矩阵是对称半正定的。 要理解Mercer定理,先要了解什么是半正定矩阵;要了解半正定矩阵,需要了解什么是正定矩阵。
关于正定与半正定矩阵,内容基本上是大学矩阵论中的内容,可以重新复习一下。下面给出一些正定矩阵和半正定矩阵的简单介绍。
正定矩阵:设M是n阶方阵,如果对任何非零向量zz,都有zTMz>0,其中zT表示z的转置,就称M正定矩阵。
正定矩阵的判定定理:
定理1:对称阵A为正定的充分必要条件是:A的特征值全为正。
定理2:对称阵A为正定的充分必要条件是:A的各阶顺序主子式都为正。
定理3:任意阵A为正定的充分必要条件是:A合同于单位阵。
正定矩阵的性质:
性质1:正定矩阵的任一主子矩阵也是正定矩阵。
性质2:若A为n阶对称正定矩阵,则存在唯一的主对角线元素都是正数的下三角阵L,使得A=LLT,此分解式称为 正定矩阵的楚列斯基(Cholesky)分解。
性质3:若A为n阶正定矩阵,则A为n阶可逆矩阵。
半正定矩阵的概念与正定矩阵比较相似:
半正定矩阵:一个n×n的埃尔米特矩阵M是正定的,当且仅当对于每个非零的复向量z,都有zTMz>0,则称M为正定矩阵,其中zT表示z的转置矩阵。当zTMz>0弱化为zTM≥0时,称M是半正定矩阵;
半正定矩阵的判定:若矩阵A的特征值大于等于0,则半正定。否则矩阵A为非正定。
Mercer定理的证明在下面的网址中可以查询:
http://ftp136343.host106.web522.com/a/biancheng/matlab/2013/0120/648.html
3、损失函数
支持向量机(SVM)是90年代中期发展起来的基于统计学习理论的一种机器学习方法,通过寻求结构化风险最小来提高学习机泛化能力,实现经验风险和置信范围的最小化,从而达到在统计样本量较少的情况下,亦能获得良好统计规律的目的。
可能很多人并不了解结构化风险、经验风险是什么,要了解这两种风险,还得从监督学习说起。
监督学习实际上就是一个经验风险或者结构风险函数的最优化问题。风险函数度量平均意义下模型预测的好坏,模型每一次预测的好坏用损失函数来度量。
监督学习从假设空间F中,选择模型ff作为决策函数,对于给定的输入X,由输入f(X)给出相应的输出Y。参数的具体意义如下:
X:输入的数据;
f(X):输入数据后,根据模型输出的预测值;
Y:实际的输出数据;
预测值f(X)可能与真实值Y一致,也可能不一致。预测值与真实值之间的差别成都用一个损失函数来度量。损失函数被记为L(Y,f(X))。
(1) 常用损失函数
0-1损失函数
L(Y,f(X))=1,Y≠f(X)
L(Y,f(X))=0,Y=f(X)
平方损失函数
L(Y,f(X))=(Y−f(X))^2
绝对损失函数
L(Y,f(X))=|Y−f(X)|
对数损失函数
L(Y,P(Y|X))=−logP(Y|X)
(2) 经验风险与结构风险
如果给定一个训练数据集如下:
T={(x1,y1),(x2,y2),...(xi,yi)...,(xN,yN)} (3.1)
模型f(X)f(X)关于训练数据集的平均损失,称为经验风险,公式如下:
Remp(f)=1N∑i=1NL(yi,f(xi)) (3.2)
关于如何选择模型,监督学习有两种策略:经验风险最小化、结构风险最小化。
经验风险最小化的策略认为:经验风险最小的模型就是最优模型,即按照经验风险最小化的标准求取最优模型,就是求解如下最优化问题:
minf∈F1N∑i=1NL(yi,f(xi)) (3.3)
然而当样本容量很小时,经验风险最小化的策略容易产生过拟合现象。
结构风险最小化可以防止过拟合。结构风险实在经验风险的基础上,加上表示模型复杂度的惩罚项,结构风险的定义如下:
Rsrm(f)=1/N∑i=1-N L(yi,f(xi)) + λJ(f) (3.4)
式(3.4)中参数说明如下:
J(f):模型的复杂度
模型f越复杂,J(f)越大;模型越简单,J(f)越小;
也就是说,J(f)是对复杂模型的惩罚;
λ≥0:权衡经验风险和模型复杂度的系数
结构风险最小化的策略认为结构风险最小的模型就是最优模型,所以求最优模型就是求解如下所示的最优化问题:
min f∈F 1/N∑i=1-N L(yi,f(xi)) + λJ(f) (3.5)
这样监督学习问题就变成了经验风险或结构风险函数的最优化问题,如式(3.4)与(3.5)。
于是,SVM也有了第二种理解,即最优化+损失最小。如果从损失函数和优化算法角度看SVM, boosting, LR等算法,可能会有不同收获。
4、最小二乘法
(1) 最小二乘法的说明
最小二乘法(又称最小平方法)是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。用函数表示为下式:
minx→∑i=1-n (ym−yi)^2 (4.1)
误差可以被定义为预测值与实际真实值的差量,所以最小二乘法就是使误差平方和达到最小,以寻求估计值的方法。用最小二乘法得到的估计,就叫做最小二乘估计。当然,取平方和作为目标函数只是众多可取的方法之一。
最小二乘法的一般形式,可以表示成下式:
minx→ ∥ym−→−y→∥2 (4.2)
有效的最小二乘法,基本思想就是认为测量中有误差,所以所有方程的累计误差为:
累积误差=∑(观测值−理论值)^2
我们求解出导致累计误差最小的参数即可:
β^= argminβ∑i=1-n ei^2
= β^ = argminβ∑i=1-n [yi−(β0+β1x1i+...+βpxpi)]^2 (4.3)
最小二乘法的优点如下:
最小二乘使得误差平方和最小,并在各个方程的误差之间建立了平衡,防止某一个极端误差取得支配地位;
计算中只要求偏导后求解线性方程组,计算过程明确便捷;
最小二乘可以导出算术平均值作为估计值;
对于上面的最后一点,从统计学角度来看,是很重要的一个性质。推理如下:
假设真值为θ,x1,…,xn是测量值。每次测量的误差为ei=xi−θ,那么按照最小二乘法,累计误差为:
L(θ)=∑i=1-n ei^2 = ∑i=1-n (xi−θ)^2 (4.4)
求解θ使L(θ)最小,结果正好是其算术平均值:x¯=(∑i−1-n xi)/n。
由于算术平均是一个历经考验的方法,而以上的推理说明,算术平均是最小二乘的一个特例,所以从另一个角度说明了最小二乘方法的优良性,使我们对最小二乘法更加有信心。
最小二乘法发表之后很快得到了大家的认可接受,并迅速的在数据分析实践中被广泛使用。不过历史上又有人把最小二乘法的发明归功于高斯,这又是怎么一回事呢。高斯在1809年也发表了最小二乘法,并且声称自己已经使用这个方法多年。高斯发明了小行星定位的数学方法,并在数据分析中使用最小二乘方法进行计算,准确的预测了谷神星的位置。
说了这么多,貌似跟本文主题SVM没有关系。后文会将最小二乘法与SVM联系在一起。本质上说,最小二乘法即是一种参数估计方法,说到参数估计,咱们得从一元线性模型说起。
(2) 最小二乘法的解法
什么是一元线性模型呢? 这里引用一元线性模型的一篇博客,来梳理下几个基本概念:
参考地址:《一元线性回归模型与最小二乘法及其C++实现 》
监督学习中,如果预测的变量是离散的,我们称其为分类(如决策树,支持向量机等);如果预测的变量是连续的,我们称其为回归;
回归分析中,如果只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析;
如果回归分析中包括两个或两个以上的自变量,且因变量和自变量之间是线性关系,则称为多元线性回归分析。
对于二维空间线性是一条直线;对于三维空间线性是一个平面,对于多维空间线性是一个超平面;
对于一元线性回归模型,假设从总体中获取了n组观察值(X1,Y1),(X2,Y2),…,…,(Xn,Yn)。对于平面中的这n个点,可以使用无数条曲线来拟合。要求样本回归函数尽可能好地拟合这组值。综合起来看,这条直线处于样本数据的中心位置最合理。
选择最佳拟合曲线的标准可以确定为:使总的拟合误差(即总残差)达到最小。有以下三个标准可以选择:
用“残差和最小”确定直线位置是一个途径。但很快发现计算“残差和”存在相互抵消的问题;
用“残差绝对值和最小”确定直线位置也是一个途径,但绝对值的计算比较麻烦;
最小二乘法的原则是以“残差平方和最小”确定直线位置,用最小二乘法除了计算比较方便外,得到的估计量还具有优良特性。这种方法对异常值非常敏感。
最常用的是普通最小二乘法(Ordinary Least Square, OLS):所选择的回归模型应该使所有观察值的残差平方和达到最小,即采用平方损失函数。
我们定义样本回归模型为:
Yi=β0^+β1^Xi+ei
转换上式为:
ei=Yi−β0^−β1^Xi (4.5)
其中,ei为样本(Xi,Yi)的误差。
接着,我们定义平方损失函数Q:
Q = ∑i=1-n ei^2 = ∑i=1-n (Yi−Yi^)2 = ∑i=1-n (Yi−β0^−β1^Xi)^2 (4.6)
则我们通过Q最小确定这条直线,就可以确定β0^ , β1^ ,以β0^ ,β1^ 为变量,把它们看做是Q的函数,就变成了一个求极值的问题。β0^ ,β1^可以通过求导得到。
令Q对β0^ ,β1^求偏导得到:
∂Q∂β0^ = 2∑i=1-n (Yi−β0^−β1^Xi)(−1) = 0
∂Q∂β1^ = 2∑i=1-n (Yi−β0^−β1^Xi)(−Xi) = 0 (4.7)
解得:
∂Q∂β0^ = (n∑ni=1-n XiYi + ∑i=1-n Xi∑i=1-n Yi ) / (n∑i=1-n Xi^2−(∑i=1-n Xi)^2)
∂Q∂β1^ = (n∑ni=1-n XiYi − ∑i=1-n Xi∑ni=1Yi ) / (n∑i=1-n Xi^2−(∑i=1-n Xi)^2) (4.8)
这就是最小二乘法的解法,求得平方损失函数的极值点。
自此,你看到求解最小二乘法与求解SVM问题何等相似,尤其是定义损失函数,而后通过偏导求得极值。
5、SMO算法
上文中,我们提到了求解对偶问题的序列最小最优化算法SMO算法,但并未提到其具体解法。
首先回到之前没有解决的问题,即式(3.5):
max α∑i=1-n αi − 1/2∑i=1-n αiαjyiyj⟨xi,xj⟩
s.t.,0≤αi≤C,i=1,...,n
∑i=1-n αiyi=0
实际上,上式最终等价于求解:
minα Ψ(α→) = min α 1/2 ∑i=1-n ∑j=1-n yiyjK(xi→,xj→)αiαj−∑i=1-n αi
s.t.,0≤αi≤C,i=1,...,n
∑i=1-n αiyi=0 (5.1)
下面介绍上式(5.1)的推导过程。
(1) SMO算法的推导
推导SMO算法之前,我们首先定义特征到结果的输出函数如下:
u=ω→⋅x→−b (5.2)
注:其实上式(5.2)中的u和我们之前定义的f(x)=ωTx+b实质是一样的。
接着我们回顾一下在第一章第4节,最大间隔分类器部分设定的原始优化问题。由于函数间隔γ=1,所以改写式(1.1)如下式(5.3)所示:
min1/2∥ω∥^2
s.t.,yi(ωTxi+b)≥1,i=1,...,n (5.3)
按照第二章第1节的方法,对上式(5.3)的目标函数求拉格朗日函数,并令拉格朗日函数对ω,α求偏导,得到:
ω→=∑i=1-n yiαixi→
b=ω→⋅xk→−yk(对于αk>0) (5.4)
将上式(5.4)代入到(5.2)中,得到:
u = ∑i=1-n yjαjK(xj→,x→)−b (5.5)
回顾前文第二章第2节第(2)小节中的讲解,拉格朗日函数的目标函数可以转化成式(2.12),即:
max α∑i=1-n αi − 1/2∑i=1-n αiαjyiyjK(xi,xj)
s.t.,αi≥0,i=1,...,n
∑i=1-n αiyi = 0
上式也可以从max函数转化成min函数,变成:
minΨ(α→)=minα1/2∑i=1-n αiαjyiyjK(xi,xj) − ∑i=1-n αi
s.t.,αi≥0,i=1,...,n
∑i=1-n αiyi = 0 (5.6)
按照前文第二章第3节,加入松弛变量后,模型修改成式(3.3):
min1/2∥ω∥^2 + C∑i=1-n ξi
s.t.,yi(ωTxi+b)≥1−ξi,i=1,...,n
0≤ξi≤C,i=1,...,n
从而,我们的问题最终变为下式:
minΨ(α→) = min α1/2∑i=1-n αiαjyiyjK(xi,xj) − ∑i=1-n αi
s.t.,0≤ξi≤C,i=1,...,n
∑i=1-n αiyi = 0 (5.7)
下面,我们要解决的问题是在αi={α1,α2,…,αn}上求取上式(5.7)中目标函数的最小值。
为了求解这些乘子,每次从中任意抽取两个乘子α1,α2,然后固定α1,α2和以外的其它乘子{α3,α4,…,αn},使得目标函数只是关于和的函数,使得目标函数只是关于α1,α2的函数。这样不断的从一堆乘子中任意抽取两个求解,不断的迭代求解子问题,最终达到求解原问题的目的。
上式(5.7)中的Ψ(⋅)即为原对偶问题的子问题目标函数,它可以表达为:
Ψ=1/2K11α1^2 + K22α2^2 + sK12α1α2 + y1α1v1 + y2α2v2 − α1 − α2 + Ψconstant (5.8)
上式(5.8)的参数含义如下所示:
Kij=K(xi→,xj→)
vi→=∑j=3-n yjα∗jKij = ui+b∗−y1α∗1K1i−y2α∗2K2i
s=y1⋅y2
即s的值为-1或1,具体由y1,y2共同决定。
为了解决这个子问题,首要问题便是每次如何选取α1,α2。
实际上,选取的两个乘子α1,α2中,一个乘子是违反KKT条件最严重的,另外一个乘子由另外一个约束条件选取。
首先选取第一个乘子,即违反KKT条件最严重的乘子。
根据KKT条件,可以得出目标函数中αiαi取值的含义:
αi=0 ⟺ yiui≥1
0<αi注:上式(5.9)中的αi还是拉格朗日乘子。
对于上式(5.9)的解释如下:
第一种情况,表明αi是正常分类,在间隔边界内部;
第二种情况,表明αi是支持向量,在间隔边界之上;
第三种情况,表明αi在两条间隔边界之间;
而我们求的最优解需要满足KKT条件,也就是说上述三个条件全都要满足。
反过来看,以下几种情况出现时,KKT条件将不能满足: 上述三种情况,都不满足KKT条件。对于这些不满足KKT条件的αi,那么就需要对其进行更新。这可以理解成式(5.7)的第一个约束条件。 另外更新的同时还需要第二个约束条件,即∑i=1-n αiyi = 0的限制。 根据∑i=1-nαiyi = 0的限制,如果假设选择两个乘子α1,α2,并设它们更新之前分别是αold1,αold2,更新之后分别是αnew1,αnew2,那么更新前后的值需要满足以下等式,才能保证前面和为0的约束条件: 上式(5.10)中,ξ是常数。 上面两个因子不容易同时求解,所以我们可以先求第二个乘子α2的解(αnew2),得到αnew2之后,然后再用αnew2表示α1的解(αnew1)。为了求解αnew2,首先需要确定αnew2的取值范围。 假设αnew2的上下边界分别为H,LH,L,那么就有: 接下来,我们就可以综合0≤αi≤C, αnew1y1+αnew2y2=αold1y1+αold2y2=ξ这两个约束条件求取αnew2的取值范围。 当y1=y2即y1,y2同号时,同样根据αnew1y1+αnew2y2=αold1y1+αold2y2=ξ,可以得到αold1+αold2=ξ,所以有: 如此总结,根据y1,y2异号或同号,可以得到αnew2的上下界分别为: 回顾前面第二个约束条件αnew1y1+αnew2y2=αold1y1+αold2y2=ξ,令等式两边同时乘以y1,可得到: 上式(5.15)的参数说明如下: 即s的值为-1或1,具体由y1,y2共同决定。 上式(5.16)对α2求导,得到: 化简上式得到: 然后,将: 代入上式(5.17),可得到: 注:其中αnew,unc2的unc是指unclipped,意思是未剪辑,后面会有解释。 令Ei=ui−yi,表示预测值与真实值之差,再令η=K(x1→,x1→)+K(x2→,x2→)−2K(x1→,x2→),然后在上式(5.18)两端同时除以η,得到一个关于单变量α2的解: 关于α2的这个解,其实没有考虑到其约束条件0≤α2≤C,即此时的解是未经剪辑的解。此时考虑约束条件0≤α2≤C,可得到经过剪辑后的αnew2的解析解为: 求出αnew2后,便可以根据αnew1y1+αnew2y2=αold1y1+αold2y2求出α1, 第一个乘子α1,可以通过刚刚说的那三种不满足KKT条件来找; 更新的b值为: 且每次更新完两个乘子的优化后,都需要再重新计算b,以及对应的EiEi值。 (2) SMO算法的步骤 综上,总结SMO的主要步骤: 选取一对αi,αj,选取方法使用启发式方法; 那么每次迭代中,应该如何更新乘子?具体步骤如下: 计算上下界H,L: 计算Ls的二阶导数 更新Ls 计算变量α2 更新α1 知道了如何更新乘子,那么选取哪些乘子进行更新呢?具体选择方法有以下两个步骤: 第一个乘子α1,可以通过刚刚说的那三种不满足KKT条件来找;
yiui≤1(原本等价于αi=C),然而实际上αi
yiui=1(原本等价于0<αiα1newy1+α2newy2 = α1oldy1+α2oldy2 = ξ (5.10)
L≤αnew2≤H (5.11)
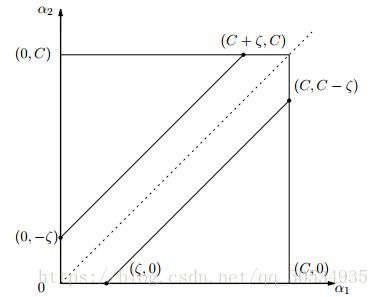
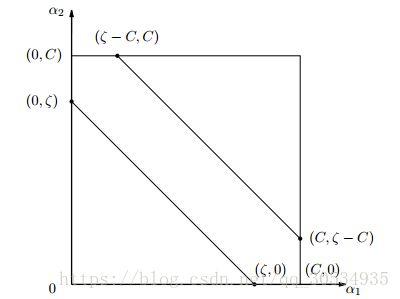
当y1≠y2即y1,y2异号时,根据αnew1y1+αnew2y2=αold1y1+αold2y2=ξ,可以得到αold1−αold2=ξ,所以有:L=max(0,−ξ),H=min(C,C−ξ) (5.12)
L=max(0,ξ−C),H=min(C,ξ) (5.13)
L=max(0,αold2−αold1),H=min(C,C+αold2−αold1),y1≠y2
L=max(0,αold2+αold1−C),H=min(C,αold2+αold1),y1=y2 (5.14)
α1+sα2=α∗1+sα∗2=w (5.15)
w=−y1∑i=3-n yiαi*
s=y1⋅y2
所以通过上式,我们可以用α2表示α1:α1=w−s⋅α2
从而把子问题的目标函数转换为只含α2的问题:Ψ=12K11(w−sα2)^2+12K22α2^2+sK12(w−sα2)α2
+ y1(w−sα2)v1−w+sα2+y2α2v2−α2+Ψconstant (5.16)
dΨ/dα2 = −sK11(w−sα2)+K22α2−K12α2+sK12(w−sα2)−y1v1+s+y2v2−1 = 0
α2(K11+K22−2K12)=s(K11−K12)w+y2(v1−v2)+1−s (5.17)
s=y1⋅y2
α1+sα2=α1∗+sα2∗=w
Kij=K(xi→,xj→)
vi→=∑j=3-n yjαj∗Kij=ui+b∗−y1α1∗K1i−y2α2∗K2i
α2new,unc(K11+K22−2K12) = α2old(K11+K22−2K12) + y2(u1−u2+y2−y1) (5.18)
α2new,unc = α2old+y2(E1−E2)η (5.19)
α2new={H,α2new,unc>H α2new,unc,L≤α2new,unc≤H L,α2new,unc
即αnew1=αold1+y1y2(αold2−αnew2)。
说到这里,那么具体应该如何选择乘子α1,α2呢?总结如下:
第二个乘子α2,可以寻找满足条件max|Ei−Ej|的乘子。
而b在满足下述条件时更新:b={b1,0<α1newb1new=bold−E1−y1(α1new−α1old)K(x1→,x1→)−y2(α2new−α2old)K(x1→,x2→)
b2new=bold−E2−y1(α1new−α1old)K(x1→,x2→)−y2(α2new−α2old)K(x2→,x2→) (5.22)
最后更新所有的αi,y,b,这样模型就出来了。从而我们就得到最开始提出的分类函数式(1.17):f(x)=∑i=1nαiyi⟨xi→,x→⟩+b
固定除αi,αj之外的其他参数,确定W极值条件下的αi,αi由αj表示。
假设某一次迭代中,需要更新x1,x2对应的拉格朗日乘子α1,α2,那么这个小规模的二次规划问题写为:Ls = maxα{(α1+α2) + ∑i=3-n αi−1/2|α1y1ϕ(x1) + α2y2ϕ(x2) + ∑i=3-n αiyiϕ(xi)|^2}
s.t.,α1y1+α2y2=−∑i=3-n αiyi,0<αiL=max(0,αold2−αold1),H=min(C,C+αold2−αold1),y1≠y2
L=max(0,αold2+αold1−C),H=min(C,αold2+αold1),y1=y2
η=2ϕ(x1)Tϕ(x2)−ϕ(x1)Tϕ(x1)−ϕ(x2)Tϕ(x2)
αnew2=αold2−y2(e1−e2)η
ei=gold(xi)−yi
如式(5.20)
αnew1=αold1+y1y2(αold2−αnew2)
第二个乘子α2,可以寻找满足条件max|Ei−Ej|的乘子。
最后,每次更新完两个乘子的优化后,都需要再重新计算b,及对应的Ei值。