梯度下降法

我们要学习一个机器学习的重要方法——梯度下降法（Gradient Descent）梯度下降法并不是一个机器学习的算法，它既不能解决回归问题，也不能解决分类问题。

那么它是什么呢？梯度下降是一种基于搜索的最优化的方法，它的目标是用于优化一个目标函数。

在机器学习中，梯度下降法的作用就是：最小化一个损失函数。

梯度下降法的模拟与可视化

 

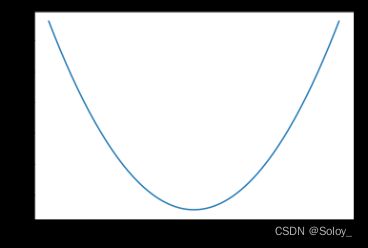
上图描述的是一个损失函数在函数不同参数取值的情况下(x轴)，对应变化值(y轴)。

对于损失函数，应该有一个最小值。对于最小化损失函数这样一个目标，实际上就是在上图所示的坐标系中，寻找合适的参数，使得损失函数的取值最小。

在这个例子是在2维平面空间上的演示，所以参数只有1个(x轴的取值)。意味着每个参数，都对应着一个损失函数值。实际上模型的参数往往不止一个，所以这个图像描述的只是损失函数优化过程的一种简单表达。

我们用代码来绘制一张这样的图

import numpy as np
import matplotlib.pyplot as plt

# 创建等差数列x,代表模型的参数取值,共150个
plot_x = np.linspace(-1., 6., 150)
print(plot_x)

[-1. -0.95302013 -0.90604027 -0.8590604 -0.81208054 -0.76510067 -0.71812081 -0.67114094 -0.62416107 -0.57718121 -0.53020134 -0.48322148 -0.43624161 -0.38926174 -0.34228188 -0.29530201 -0.24832215 -0.20134228 …… 略 …… 5.20134228 5.24832215 5.29530201 5.34228188 5.38926174 5.43624161 5.48322148 5.53020134 5.57718121 5.62416107 5.67114094 5.71812081 5.76510067 5.81208054 5.8590604 5.90604027 5.95302013 6. ]

# 通过二次方程来模拟一个损失函数的计算,plot_y值就是图形上弧线所对应的点
plot_y = (plot_x-2.5)**2 - 1

绘制图形

plt.plot(plot_x, plot_y)
plt.show()

 

下面，我们来尝试一下实现我们的梯度下降法。

首先定义一个函数，来计算损失函数对应的导数。目标就是计算参数theat的导数

def derivative(theta):
	return 2*(theta-2.5)

还需要定义一个函数来计算theat值对应的损失函数

def loss(theta):
	return (theta-2.5)**2 - 1

计算梯度值

# 以0作为theta的初始点
theta = 0.
eta = 0.1
epsilon = 1e-8
while True:
	# 计算当前theta对应点的梯度(导数)
    gradient = derivative(theta)

	# 更新theta前,先积累下上一次的theta值
    last_theta = theta

		# 更新theta,向导数的负方向移动一步，步长使用eta(学习率)来控制
    theta = theta - eta * gradient

	# 理论上theta最小值应当为0是最佳。但实际情况下，theta很难达到刚好等于0的情况
	# 所以我们可以设置一个最小值spsilon来表示我们的需要theta达到的最小值目标
    # 判断theta每次更新后,和上一个theta的差值是否已满足小于epsilon(最小值)的条件
	# 满足的话就终止运算
    if(abs(loss(theta) - loss(last_theta)) < epsilon):
        break

print(theta)
print(loss(theta))

2.499891109642585 -0.99999998814289

通过结果可以看出，当theta取2.5时候，损失函数的最小值正好对应着截距-1

学习率对梯度的影响

为了能够计算不同学习率下，theta的每一步变更值。我们对代码进行一些补充。

theta = 0.0
eta = 0.1
epsilon = 1e-8

# 添加一个记录每一步theta变更的list
theta_history = [theta]
while True:
    gradient = derivative(theta)
    last_theta = theta
    theta = theta - eta * gradient
	# 更新theta后记录它们的值
    theta_history.append(theta)
    
    if(abs(loss(theta) - loss(last_theta)) < epsilon):
        break

绘制theta每一步的变更

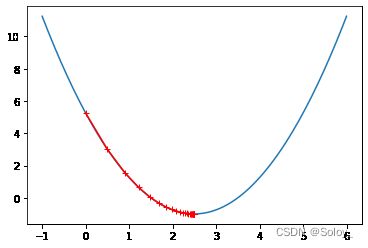
plt.plot(plot_x, loss(plot_x))
plt.plot(np.array(theta_history), loss(np.array(theta_history)), color="r", marker='+')
plt.show()

 

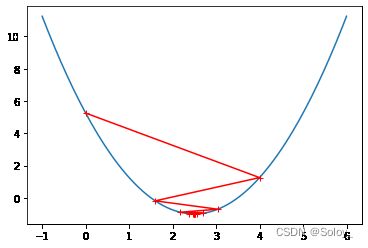
可以看到theta在下降过程中，每一步都在逐渐变小(逐渐逼近)，直到满足小于epsilon的条件。

查看一下theta_history的长度

len(theta_history)

46

我们通过梯度下降法，经过了45次查找，最终找到了theta的最小值。

为了更方便的调试eta(学习率)的值，我们对代码进行进一步的封装。把梯度下降方法和绘图分别封装为两个函数。

theta_history = []

def gradient_descent(initial_theta, eta, epsilon=1e-8):
    theta = initial_theta
    theta_history.append(initial_theta)

    while True:
        gradient = derivative(theta)
        last_theta = theta
        theta = theta - eta * gradient
        theta_history.append(theta)
    
        if(abs(loss(theta) - loss(last_theta)) < epsilon):
            break
            
def plot_theta_history():
    plt.plot(plot_x, loss(plot_x))
    plt.plot(np.array(theta_history),loss(np.array(theta_history)), color="r", marker='+')
    plt.show()

尝试更小的eta值

eta = 0.01
theta_history = []
gradient_descent(0, eta)
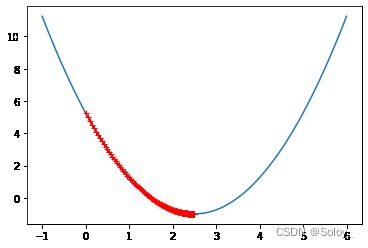
plot_theta_history()

 

theta下降的路径中，每一步的长度更短了，步数也更多了。

len(theta_history)

424

这次经过了424步才得到theta的最小值。

eta就是梯度下降中我们常常谈到的学习率learn rate(lr)。学习率的大小直接影响到梯度更新的步数。很明显，学习率越小，theta下降的步长越小。所需要的步数(计算次数)也就越多。

试试更小的学习率

eta = 0.001
theta_history = []
gradient_descent(0, eta)
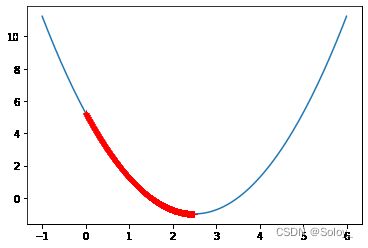
plot_theta_history()

 

步长已经短到几乎连成一条粗线

len(theta_history)

3682

共经过了3682步

那么学习率调大一些是不是更好呢？

eta = 0.8
theta_history = []
gradient_descent(0, eta)
plot_theta_history()

 

theta变成了从曲线的左侧跳到了右侧，由于eta还是够小。最终我们还是计算得到了theta的最小值。

如果更大一些的学习率，会是什么效果呢？

eta = 1.1
theta_history = []
gradient_descent(0, eta)

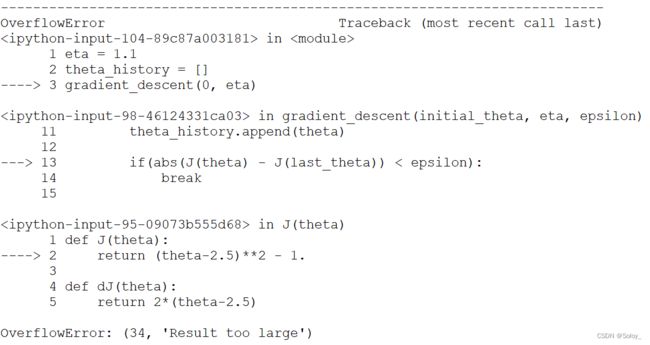
直接报错！

错误描述信息是：结果值太大了。

---

为什么会产生这样的原因呢？

原因是eta太大所导致的，theta在每次更新也会变得越来越大。梯度非但没有收敛，反而在向着反方向狂奔。直到结果值最终超出了计算机所能容纳的最大值，错误类型OverflowError(计算溢出错误)。

---

为避免计算值的溢出，我们改造损失值计算方法

def loss(theta):
    try:
        return (theta-2.5)**2 - 1.
    except:
        return float('inf') # 计算溢出时，直接返回一个float的最大值

给梯度更新方法添加一个最大循环次数

def gradient_descent(initial_theta, eta, n_iters = 1e4, epsilon=1e-8):
    
    theta = initial_theta
    i_iter = 0 # 初始循环次数
    theta_history.append(initial_theta)

    while i_iter < n_iters: # 小于最大循环次数
        gradient = derivative(theta)
        last_theta = theta
        theta = theta - eta * gradient
        theta_history.append(theta)
    
        if(abs(loss(theta) - loss(last_theta)) < epsilon):
            break
            
        i_iter += 1  # 循环次数+1

重新执行刚刚会报错的

eta = 1.1
theta_history = []
gradient_descent(0, eta)

没有错误了~

len(theta_history)

10001

达到最大循环次数后，梯度计算就停止了。

为了观察eta=1.1时，theta到底是如何更新的。我们指定一个有限的梯度更新次数(10次)

eta = 1.1
theta_history = []
gradient_descent(0, eta, n_iters=10)
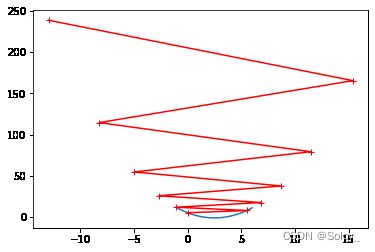
plot_theta_history()

 

theta的值从曲线出发，逐渐向外。最终越变越大……

学习率的最佳取值

学习率eta的取值，是不是1就是极限值呢？

实际上eta的取值是和损失函数相关的，或者说时和theta的导数相关的。所以没有一个固定标准。

所以，学习率对于梯度下降法来说也是一个超参数。也需要网格搜索来寻找。

保险的方法，是把eta先设置为0.01，然后逐渐寻找它的最佳取值。大多数函数，都是可以胜任的。

如果出现了参数值过大，也可以用上面的方法绘制图形来查看哦~