深度学习——目标检测基础知识

一，anchors

所谓 anchors，实际上就是一组由 generate_anchors.py 生成的矩形框。其中每行的4个值 (x1,y1,x2,y2) 表矩形左上和右下角点坐标。9 个矩形共有 3 种形状，长宽比为大约为 {1:1, 1:2, 2:1} 三种, 实际上通过anchors就引入了检测中常用到的多尺度方法。给模型提供一种尺寸先验。
generate_anchors.py` 的代码如下：

def generate_anchor_base(base_size=16, ratios=[0.5, 1, 2],
                         anchor_scales=[8, 16, 32]):
    """Generate anchor base windows by enumerating aspect ratio and scales.

    Generate anchors that are scaled and modified to the given aspect ratios.
    Area of a scaled anchor is preserved when modifying to the given aspect
    ratio.

    :obj:`R = len(ratios) * len(anchor_scales)` anchors are generated by this
    function.
    The :obj:`i * len(anchor_scales) + j` th anchor corresponds to an anchor
    generated by :obj:`ratios[i]` and :obj:`anchor_scales[j]`.

    For example, if the scale is :math:`8` and the ratio is :math:`0.25`,
    the width and the height of the base window will be stretched by :math:`8`.
    For modifying the anchor to the given aspect ratio,
    the height is halved and the width is doubled.

    Args:
        base_size (number): The width and the height of the reference window.
        ratios (list of floats): This is ratios of width to height of
            the anchors.
        anchor_scales (list of numbers): This is areas of anchors.
            Those areas will be the product of the square of an element in
            :obj:`anchor_scales` and the original area of the reference
            window.

    Returns:
        ~numpy.ndarray:
        An array of shape :math:`(R, 4)`.
        Each element is a set of coordinates of a bounding box.
        The second axis corresponds to
        :math:`(x_{min}, y_{min}, x_{max}, y_{max})` of a bounding box.

    """
    import numpy as np
    py = base_size / 2.
    px = base_size / 2.

    anchor_base = np.zeros((len(ratios) * len(anchor_scales), 4),
                           dtype=np.float32)
    for i in six.moves.range(len(ratios)):
        for j in six.moves.range(len(anchor_scales)):
            h = base_size * anchor_scales[j] * np.sqrt(ratios[i])
            w = base_size * anchor_scales[j] * np.sqrt(1. / ratios[i])

            index = i * len(anchor_scales) + j
            anchor_base[index, 0] = px - w / 2.
            anchor_base[index, 1] = py - h / 2.

            anchor_base[index, 2] = px + h / 2.
            anchor_base[index, 3] = py + w / 2.
    return anchor_base
    if __name__ == "__main__":
    bbox_list = generate_anchor_base()
    print(bbox_list)

交并比IOU

$$IoU=\frac{\mathrm{area}(C)\cap \mathrm{area}(G)}{\mathrm{area}(C)\cup \mathrm{area}(G)}$$
交并比（Intersection-over-Union，IoU），目标检测中使用的一个概念，是产生的候选框（candidate bound）与原标记框（ground truth bound）的交叠率，即它们的交集与并集的比值。最理想情况是完全重叠，即比值为1。计算公式如下：

代码实现如下：

# _*_ coding:utf-8 _*_
# 计算iou

"""
bbox的数据结构为(xmin,ymin,xmax,ymax)--(x1,y1,x2,y2),
每个bounding box的左上角和右下角的坐标
输入：
    bbox1, bbox2: Single numpy bounding box, Shape: [4]
输出：
    iou值
"""
import numpy as np
import cv2

def iou(bbox1, bbox2):
    """
    计算两个bbox(两框的交并比)的iou值
    :param bbox1: (x1,y1,x2,y2), type: ndarray or list
    :param bbox2: (x1,y1,x2,y2), type: ndarray or list
    :return: iou, type float
    """
    if type(bbox1) or type(bbox2) != 'ndarray':
        bbox1 = np.array(bbox1)
        bbox2 = np.array(bbox2)

    assert bbox1.size == 4 and bbox2.size == 4, "bounding box coordinate size must be 4"
    xx1 = np.max((bbox1[0], bbox2[0]))
    yy1 = np.max((bbox1[1], bbox1[1]))
    xx2 = np.min((bbox1[2], bbox2[2]))
    yy2 = np.min((bbox1[3], bbox2[3]))
    bwidth = xx2 - xx1
    bheight = yy2 - yy1
    area = bwidth * bheight  # 求两个矩形框的交集
    union = (bbox1[2] - bbox1[0])*(bbox1[3] - bbox1[1]) + (bbox2[2] - bbox2[0])*(bbox2[3] - bbox2[1]) - area  # 求两个矩形框的并集
    iou = area / union

    return iou


if __name__=='__main__':
    rect1 = (461, 97, 599, 237)
    # (top, left, bottom, right)
    rect2 = (522, 127, 702, 257)
    iou_ret = round(iou(rect1, rect2), 3) # 保留3位小数
    print(iou_ret)

    # Create a black image
    img=np.zeros((720,720,3), np.uint8)
    cv2.namedWindow('iou_rectangle')
    """
    cv2.rectangle 的 pt1 和 pt2 参数分别代表矩形的左上角和右下角两个点,
    coordinates for the bounding box vertices need to be integers if they are in a tuple,
    and they need to be in the order of (left, top) and (right, bottom). 
    Or, equivalently, (xmin, ymin) and (xmax, ymax).
    """
    cv2.rectangle(img,(461, 97),(599, 237),(0,255,0),3)
    cv2.rectangle(img,(522, 127),(702, 257),(0,255,0),3)
    font  = cv2.FONT_HERSHEY_SIMPLEX
    cv2.putText(img, 'IoU is ' + str(iou_ret), (341,400), font, 1,(255,255,255),1)
    cv2.imshow('iou_rectangle', img)
    cv2.waitKey(0)

三，NMS 算法

在目标检测中，常会利用非极大值抑制算法(NMS，non maximum suppression)对生成的大量候选框进行后处理，去除冗余的候选框，得到最佳检测框，以加快目标检测的效率。其本质思想是其思想是搜素局部最大值，抑制非极大值。非极大值抑制，在计算机视觉任务中得到了广泛的应用，例如边缘检测、人脸检测、目标检测（DPM，YOLO，SSD，Faster R-CNN）等。即如下图所示实现效果，消除多余的候选框，找到最佳的 bbox。NMS过程如下图所示：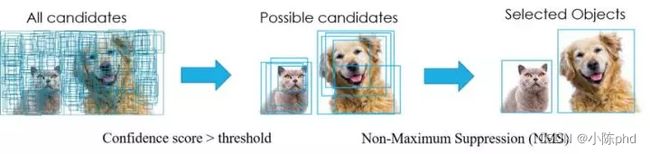
NMS 主要就是通过迭代的形式，不断地以最大得分的框去与其他框做 IoU 操作，并过滤那些 IoU 较大的框。

其实现的思想主要是将各个框的置信度进行排序，然后选择其中置信度最高的框 A，将其作为标准选择其他框，同时设置一个阈值，当其他框B与A的重合程度超过阈值就将 B 舍弃掉，然后在剩余的框中选择置信度最大的框，重复上述操作。算法过程如下：

1. 根据候选框类别分类概率排序：F>E>D>C>B>A，并标记最大概率的矩形框F作为标准框。
2. 分别判断 A~E 与 F 的重叠度 IOU (两框的交并比)是否大于某个设定的阈值，假设 B、D 与 F 的重叠度超过阈值，那么就扔掉 B、D；
3. 从剩下的矩形框 A、C、E中，选择概率最大的 E，标记为要保留下来的，然后判读 E 与 A、C 的重叠度，扔掉重叠度超过设定阈值的矩形框；
4. 对剩下的 bbox，循环执行(2)和(3)直到所有的 bbox 均满足要求（即不能再移除 bbox）

import numpy as np

def py_nms(dets, thresh):
    """Pure Python NMS baseline.注意，这里的计算都是在矩阵层面上计算的
    greedily select boxes with high confidence and overlap with current maximum <= thresh
    rule out overlap >= thresh
    :param dets: [[x1, y1, x2, y2 score],] # ndarray, shape(-1,5)
    :param thresh: retain overlap < thresh
    :return: indexes to keep
    """
    # x1、y1、x2、y2、以及score赋值
    x1 = dets[:, 0]
    y1 = dets[:, 1]
    x2 = dets[:, 2]
    y2 = dets[:, 3]

    # 计算每一个候选框的面积, 纯矩阵加和乘法运算,为何加1？
    areas = (x2 - x1 + 1) * (y2 - y1 + 1)
    # order是将confidence降序排序后得到的矩阵索引
    order = np.argsort(dets[:, 4])[::-1]
    keep = []
    while order.size > 0:
        i = order[0]
        keep.append(i)
        # 计算当前概率最大矩形框与其他矩形框的相交框的坐标，会用到numpy的broadcast机制，得到的是向量
        xx1 = np.maximum(x1[i], x1[order[1:]])
        yy1 = np.maximum(y1[i], y1[order[1:]])
        xx2 = np.minimum(x2[i], x2[order[1:]])
        yy2 = np.minimum(y2[i], y2[order[1:]])

        # 计算相交框的面积,注意矩形框不相交时w或h算出来会是负数，用0代替
        w = np.maximum(0.0, xx2 - xx1 + 1)
        h = np.maximum(0.0, yy2 - yy1 + 1)
        inter = w * h
        # 计算重叠度IOU：重叠面积/（面积1+面积2-重叠面积）
        iou = inter / (areas[i] + areas[order[1:]] - inter)
        # 找到重叠度不高于阈值的矩形框索引
        inds = np.where(iou < thresh)[0]
        # 将order序列更新，由于前面得到的矩形框索引要比矩形框在原order序列中的索引小1，所以要把这个1加回来
        order = order[inds + 1]
    return keep

# test
if __name__ == "__main__":
    dets = np.array([[30, 20, 230, 200, 1],
                     [50, 50, 260, 220, 0.9],
                     [210, 30, 420, 5, 0.8],
                     [430, 280, 460, 360, 0.7]])
    thresh = 0.35
    keep_dets = py_nms(dets, thresh)
    print(keep_dets)
    print(dets[keep_dets])

Soft NMS算法

Soft NMS算法是对NMS算法的改进，是发表在ICCV2017的文章中提出的。NMS算法存在一个问题是可能会把一些目标框给过滤掉，从而导致目标的recall指标比较低。原来的NMS可以描述如下：将IOU大于阈值的窗口的得分全部置为0，计算公式如下：$$s_i=\{\begin{array}{ll}{s}_i,& \mathrm{iou}\left(\mathcal{M},b_i\right)<N_t\\ 0,& \mathrm{iou}\left(\mathcal{M},b_i\right)\ge N_t\end{array}$$

改进有两种形式，一种是线性加权的。设 si 为第 i 个 box 的 score, 则在应用 SoftNMS 时各个 box score 的计算公式如下：
$$s_i=\{\begin{array}{ll}{s}_i,& \mathrm{iou}\left(\mathcal{M},b_i\right)<N_t\\ s_i\left(1-\mathrm{iou}\left(\mathcal{M},b_i\right)\right),& \mathrm{iou}\left(\mathcal{M},b_i\right)\ge N_t\end{array}$$
另一种是高斯加权的，高斯惩罚系数(与上面的线性截断惩罚不同的是, 高斯惩罚会对其他所有的 box 作用)，计算公式图如下：
$$s_i=s_i{e}^{-\frac{\mathrm{iou}{\left(\mathcal{M},b_i\right)}^2}{\sigma }},\forall b_i\notin \mathcal{D}$$
注意，这两种形式，思想都是M为当前得分最高框，$b_i$为待处理框， $b_i$和M的IOU越大，bbox的得分$s_i$就下降的越厉害($N_t$为给定阈值)。

def soft_nms(dets, thresh, type='gaussian'):
    x1 = dets[:, 0]
    y1 = dets[:, 1]
    x2 = dets[:, 2]
    y2 = dets[:, 3]
    scores = dets[:, 4]

    areas = (x2 - x1 + 1) * (y2 - y1 + 1)
    order = scores.argsort()[::-1]
    scores = scores[order]

    keep = []
    while order.size > 0:
        i = order[0]
        dets[i, 4] = scores[0]
        keep.append(i)

        xx1 = np.maximum(x1[i], x1[order[1:]])
        yy1 = np.maximum(y1[i], y1[order[1:]])
        xx2 = np.minimum(x2[i], x2[order[1:]])
        yy2 = np.minimum(y2[i], y2[order[1:]])

        w = np.maximum(0.0, xx2 - xx1 + 1)
        h = np.maximum(0.0, yy2 - yy1 + 1)
        inter = w * h
        # 计算重叠度IOU：重叠面积/（面积1+面积2-重叠面积）
        ovr = inter / (areas[i] + areas[order[1:]] - inter)

        order = order[1:]
        scores = scores[1:]
        if type == 'linear':
            inds = np.where(ovr >= thresh)[0]
            scores[inds] *= (1 - ovr[inds])
        else:
            scores *= np.exp(- ovr ** 2 / thresh)
        inds = np.where(scores > 1e-3)[0]
        order = order[inds]
        scores = scores[inds]

        tmp = scores.argsort()[::-1]
        order = order[tmp]
        scores = scores[tmp]
    return keep

评价指标

mAP定义及相关概念

评价指标	定义及理解
mAP	mean Average Precision, 即各类别AP的平均值
AP	PR曲线下面积，后文会详细讲解
PR曲线	Precision-Recall曲线
Precision	TP / (TP + FP)
Recall	TP / (TP + FN)
TP	IoU>0.5的检测框数量（同一Ground Truth只计算一次）
FP	IoU<=0.5的检测框，或者是检测到同一个GT的多余检测框的数量
FN	没有检测到的GT的数量

一，评价标准的基本概念

为了了解模型的泛化能力，即判断模型的好坏，我们需要用某个指标来衡量，有了评价指标，就可以对比不同模型的优劣，并通过这个指标来进一步调参优化模型。对于分类和回归两类监督模型，分别有各自的评判标准。

1.1，准确率、精确率、召回率、F1

准确率

准确率 – Accuracy，预测正确的结果占总样本的百分比，公式如下：$准确率=(TP+TN)/(TP+TN+FP+FN)$.

虽然准确率可以判断总的正确率，但是在样本不平衡 的情况下，并不能作为很好的指标来衡量结果。举个简单的例子，比如在一个总样本中，正样本占 90%，负样本占 10%，样本是严重不平衡的。对于这种情况，我们只需要将全部样本预测为正样本即可得到 90% 的高准确率，但实际上我们并没有很用心的分类，只是随便无脑一分而已。这就说明了：由于样本不平衡的问题，导致了得到的高准确率结果含有很大的水分。即如果样本不平衡，准确率就会失效。

精确率、召回率

精确率（查准率）P、召回率（查全率）R 的计算涉及到混淆矩阵的定义，混淆矩阵表格如下：

名称	定义
True Positive(真正例, TP)	将正类预测为正类数
True Negative(真负例, TN)	将负类预测为负类数
False Positive(假正例, FP)	将负类预测为正类数 → 误报 (Type I error)
False Negative(假负例子, FN)	将正类预测为负类数 → 漏报 (Type II error)

查准率与查全率计算公式：

• 查准率（精确率）P = TP/(TP+FP)
• 查全率（召回率）R = TP/(TP+FN)

精准率和准确率看上去有些类似，但是完全不同的两个概念。精准率代表对正样本结果中的预测准确程度，而准确率则代表整体的预测准确程度，既包括正样本，也包括负样本。

精确率描述了模型有多准，即在预测为正例的结果中，有多少是真正例；召回率则描述了模型有多全，即在为真的样本中，有多少被我们的模型预测为正例。精确率和召回率的区别在于分母不同，一个分母是预测为正的样本数，另一个是原来样本中所有的正样本数。

1.2，PR曲线图

精准率和召回率的关系可以用一个 P-R 图来展示，以查准率 P 为纵轴、查全率 R 为横轴作图，就得到了查准率－查全率曲线，简称P-R曲线，PR 曲线下的面积定义为 AP:

1.3，如何理解 P-R曲线

可以从排序型模型或者分类模型理解。以逻辑回归举例，逻辑回归的输出是一个 0 到 1 之间的概率数字，因此，如果我们想要根据这个概率判断用户好坏的话，我们就必须定义一个阈值 。通常来讲，逻辑回归的概率越大说明越接近 1，也就可以说他是坏用户的可能性更大。比如，我们定义了阈值为 0.5，即概率小于 0.5 的我们都认为是好用户，而大于 0.5 都认为是坏用户。因此，对于阈值为 0.5 的情况下，我们可以得到相应的一对查准率和查全率。
但问题是：这个阈值是我们随便定义的，我们并不知道这个阈值是否符合我们的要求。 因此，为了找到一个最合适的阈值满足我们的要求，我们就必须遍历 0 到 1 之间所有的阈值，而每个阈值下都对应着一对查准率和查全率，从而我们就得到了这条曲线。

有的朋友又问了：如何找到最好的阈值点呢？ 首先，需要说明的是我们对于这两个指标的要求：我们希望查准率和查全率同时都非常高。 但实际上这两个指标是一对矛盾体，无法做到双高。图中明显看到，如果其中一个非常高，另一个肯定会非常低。选取合适的阈值点要根据实际需求，比如我们想要高的查全率，那么我们就会牺牲一些查准率，在保证查全率最高的情况下，查准率也不那么低。

1.4，PR、ROC曲线与AUC面积

• PR 曲线是以 Recall 为横轴，Precision 为纵轴；而 ROC曲线则是以 FPR 为横轴，TPR 为纵轴**。P-R 曲线越靠近右上角性能越好。
• PR 曲线展示的是Precision vs Recall 的曲线，ROC 曲线展示的是 FPR（x 轴：False positive rate） vs TPR（True positive rate, TPR）曲线。
• P、R 和 F1 指标评价在信息检索中用的比较多，在机器学习中还有一种 ROC 曲线来评价性能。
• PR 曲线与 ROC 曲线的相同点是都采用了 TPR (Recall)，都可以用 AUC 来衡量分类器的效果。不同点是 ROC 曲线使用了 FPR，而 PR 曲线使用了 Precision，因此PR曲线的两个指标都聚焦于正例。类别不平衡问题中由于主要关心正例，所以在此情况下PR曲线被广泛认为优于ROC曲线。### 1.5，F1-Score

如果想要找到 $P$ 和 $R$ 二者之间的一个平衡点，我们就需要一个新的指标：$F1$ 分数。$F1$ 分数同时考虑了查准率和查全率，让二者同时达到最高，取一个平衡。$F1$ 计算公式如下：

$$F1=\frac{2\ast P\ast R}{P+R}=\frac{2\ast TP}{样例总数+TP-TN}$$

$F1$ 度量的一般形式：$F_{\beta }$，能让我们表达出对查准率/查全率的偏见，$F_{\beta }$计算公式如下：

$$F_{\beta }=\frac{1+{\beta }^2\ast P\ast R}{({\beta }^2\ast P)+R}$$

其中 $\beta >1$ 对查全率有更大影响，$\beta <1$ 对查准率有更大影响。

不同的计算机视觉问题，对两类错误有不同的偏好，常常在某一类错误不多于一定阈值的情况下，努力减少另一类错误。在目标检测中，mAP（mean Average Precision）作为一个统一的指标将这两种错误兼顾考虑。

1.6，二分类、多分类指标计算

二分类

$$F1score=\frac{2\times P\times R}{(P+R)}$$
其中，准确率(precise) $P=TP/(TP+FP)$，召回率(recall) $R=TP/(TP+FN)$.

多分类

• Macro F1: 将 n 分类的评价拆成 n 个二分类的评价，计算每个二分类的 F1 score，n 个 F1 score 的平均值即为 Macro F1。
• Micro F1: 将 n 分类的评价拆成 n 个二分类的评价，将 n 个二分类评价的TP、FP、RN对应相加，计算评价准确率和召回率，由这 2 个准确率和召回率计算的F1 score 即为 Micro F1。
• 一般来讲，Macro F1、Micro F1 值高的分类效果好。Macro F1受样本数量少的类别影响大。

1.7，mAP指标理解

AP 衡量的是训练好的模型在每个类别上的好坏，mAP 衡量的是模型在所有类别上的好坏，得到 AP 后 mAP 的计算就变得很简单了，就是取所有 AP 的平均值。AP 的计算公式比较复杂（所以单独作一章节内容），详细内容参考下文。

mAP 这个术语有不同的定义。此度量指标通常用于信息检索、图像分类和目标检测领域。然而这两个领域计算 mAP 的方式却不相同。这里我们只谈论目标检测中的 mAP 计算方法。

mAP 常作为目标检测算法的评价指标，具体来说就是，对于每张图片检测模型会输出多个预测框（远超真实框的个数），我们使用 IoU (Intersection Over Union，交并比)来标记预测框是否预测准确。标记完成后，随着预测框的增多，查全率 R 总会上升，在不同查全率 R 水平下对准确率 P 做平均，即得到AP，最后再对所有类别按其所占比例做平均，即得到 mAP 指标。

• 目标检测评价标准-AP mAP
• 目标检测的性能评价指标
• Soft-NMS
• Recent Advances in Deep Learning for Object Detection
• A Simple and Fast Implementation of Faster R-CNN
• 分类模型评估指标——准确率、精准率、召回率、F1、ROC曲线、AUC曲线
• 一文让你彻底理解准确率，精准率，召回率，真正率，假正率，ROC/AUC