scikit-learn机器学习九(特征工程)
sk-learn机器学习之特征工程
- 特征选择
- 过滤法
-
- 低方差特征
- 卡方检验
- 包装法
-
- 递归特征消除
- 嵌入法
-
- 基于惩罚的特征选择
- 基于树模型的特征选择
- 降维
-
- PCA
- LDA
特征选择
当我们完成了数据预处理之后,我们就可以根据需要选择合适的特征带入机器学习算法和模型中训练,一般我们从两个方面来考虑: 特征的相关性和特征的离散程度
基于以上两个基本思想,我们一般有三种特征选择的方法:
- 过滤法:通过对离散程度和相关性的评分,来选择特征
- 包装法:根据预测结果,我们每次选择或者排除掉一些特征来反复优化结果
- 嵌入法:先进行模型的训练,然后得到各个特征的权值系数(就像决策树中的feature_importances_
)然后再选择特征
过滤法
低方差特征
这个很好理解:方差低的特征说明该特征的大部分数据集中在一起,那么该特征对模型的训练作用不大
具体代码:
from sklearn.feature_selection import VarianceThreshold
import numpy as np
# 导入库
x = np.array([[1, 1, 2, 9], [1, 2, 3, 15],
[1, 5, 6, 0], [1, 10, 12, 2]])
print(x)
# 输入矩阵
re = VarianceThreshold(threshold=1).fit_transform(x)
print(re)
# 打印筛选后的数据
输出结果:
[[ 1 1 2 9]
[ 1 2 3 15]
[ 1 5 6 0]
[ 1 10 12 2]]
[[ 1 2 9]
[ 2 3 15]
[ 5 6 0]
[10 12 2]]
第一列特征都是1,方差为0,低于阈值(threshold=3),所以生成的矩阵中没有第一列
卡方检验
适用于分类问题中y离散的情况
用于检验自变量和因变量的相关性,返回最好的K个特征
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2
from sklearn.datasets import load_breast_cancer
# 使用sklearn自带的数据库
iris = load_breast_cancer()
x, y = iris.data, iris.target
print(x.shape)
x_new = SelectKBest(chi2, k=10).fit_transform(x, y)
# 通过统计相关性选取最好的十个特征
print(x_new.shape)
# 打印选择好后的shape
结果:
(569, 30)
(569, 10)
# 只剩下十个特征
包装法
主要思想:根据不同特征的组合筛选出最优的特征组合方法
递归特征消除
from sklearn.svm import SVC
from sklearn.datasets import load_iris
from sklearn.feature_selection import RFE
# 我们使用鸢尾花数据集
iris = load_iris()
x, y = iris.data, iris.target
svc = SVC(kernel="linear", C=1)
rfe = RFE(estimator=svc, n_features_to_select=2, step=1)
# 第一个参数是模型选择
# 第二个参数是选择几个特征
# 第三个参数是每次迭代去掉几个特征
rfe.fit(x, y)
print(rfe.ranking_)
输出结果:
[3 2 1 1]
# 两个1表明选择的两个最重要的特征,其他的特征再依次排名
注意这里使用不同的estimator会有不同的排名结果
嵌入法
基于惩罚的特征选择
使用带惩罚项的基模型,不仅能够筛选出特征,还同时进行了降维
惩罚项一般有L1 L2,具体可以参考最后给出的链接中的例子
from sklearn.feature_selection import SelectFromModel
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import load_iris
SelectFromModel(LogisticRegression(penalty="l1", C=0.1)).fit_transform(iris.data, iris.target)
基于树模型的特征选择
这里就是运用树模型中特有的属性importance_来查看特征的权重再根据需要提取特征
降维
这里顺便再提一下降维,降维能够更好的让数据适配模型,也能够降低模型的计算量和计算时间,一般我们有两种方法:PCA LDA
两种方法都是将样本映射到低维度,但是PCA是为了让映射后的样本具有最大的发散性,而LDA是为了让映射后的样本有最好的分类性能
PCA
具体例子可以参考我的另一篇文章,里面有详细讲解:
scikit-learn机器学习七 (SVM,K-均值算法,PCA)
LDA
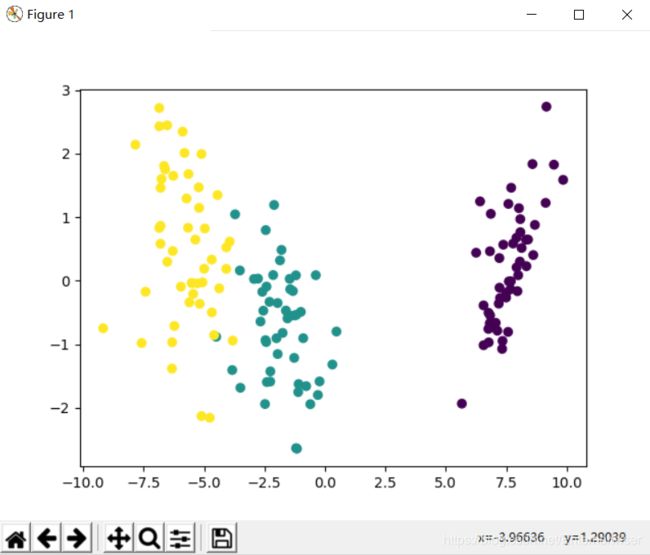
这里我们继续使用鸢尾花数据集,将它降维成二维,然后使用matplotlib进行可视化
# LDA是有监督的降维方法,但是不可用于回归分析
# PCA是无监督的降维方法
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
iris = load_iris()
category = pd.Categorical(iris.target)
# 将标签进行量化
lda = LinearDiscriminantAnalysis(n_components=2)
# 参数n_components为降维后的维数
x_lda = lda.fit_transform(iris.data, iris.target)
print(x_lda.shape)
print(x_lda[:10]) # 返回前十
plt.scatter(x_lda[:, 0], x_lda[:, 1], c=category.codes)
plt.show()
(150, 2)
# 只剩下两个特征(二维)
[[ 8.06179978 0.30042062]
[ 7.12868772 -0.78666043]
[ 7.48982797 -0.26538449]
[ 6.81320057 -0.67063107]
[ 8.13230933 0.51446253]
[ 7.70194674 1.46172097]
[ 7.21261762 0.35583621]
[ 7.60529355 -0.01163384]
[ 6.56055159 -1.01516362]
[ 7.34305989 -0.94731921]]
# 返回的前十组数据
如何选择PCA和LDA呢?
一般来说,如果数据是有类别标签的,那么优先选择LDA去尝试降维;如果没有类别标签,那么PCA优先
至此,特征工程的知识基本结束啦,大家多动手实践哟!!!
跟另一篇文章一起食用会事半功倍哟!
scikit-learn机器学习八 (数据预处理)
本文章参考:
总结:sklearn机器学习之特征工程
点个赞呗!