机器学习之特征工程(特征选择)
接上篇:
机器学习之特征工程(数据清洗)
文章目录
-
- 1、Filter(过滤法)
-
- 1.1、方差选择法
- 1.2、相关系数法
- 1.3、卡方检验
- 1.4、互信息法
- 2、Wrapper(包装法)
-
- 2.1、递归特征消除法
- 3、Embedded(嵌入法)
-
- 3.1、基于惩罚项的特征选择法
- 3.2、基于树模型的特征选择
- 4、降维方法
- 全篇数据集以sklearn自带数据集手写体识别为例进行说明。数据集中:包含64个特征变量及1个因变量y。
import numpy as np
from scipy.stats import pearsonr
from sklearn.feature_selection import SelectKBest
from sklearn.datasets import load_digits
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
data = pd.DataFrame(load_digits().data)
data.columns = [f'x{i}' for i in range(1,65)]
data['y'] = load_digits().target
data.head(3)
1、Filter(过滤法)
思路:使用某种独立于数据挖掘任务的方法,在数据挖掘过程前进行特征提取,尽可能使特征之间的相关度较低。
- 按照相关性对各特征评分,设定阈值或特征个数进行筛选,分为单变量过滤方法和多变量过滤方法。
- 单变量过滤方法:不考虑特征间的相关性,只研究特征变量和目标变量间的相关性对特征进行排序,过滤掉最不相关的特征变量。优点是计算效率高、不易过拟合。
- 多变量过滤方法:考虑特征之间的相关性,不依赖于任何机器学习方法,且不需要交叉验证。
- 过滤法的优点:计算效率比较高;缺点:没有考虑机器学习算法的特点。
1.1、方差选择法
- 先计算各个特征的方差,然后根据阈值,选择方差大于阈值的特征
from sklearn.feature_selection import VarianceThreshold
# 方差选择法,返回值为特征选择后的数据
# 参数threshold为方差的阈值
v = VarianceThreshold(threshold=30) # 指定方差大于30
vv = v.fit_transform(data.iloc[:,0:64]) # 拟合选取特征
vv.shape,v.get_support(),vv # 维度 是否为选取的特征 提取后的数据
# 方差大于30的特征含有21个
1.2、相关系数法
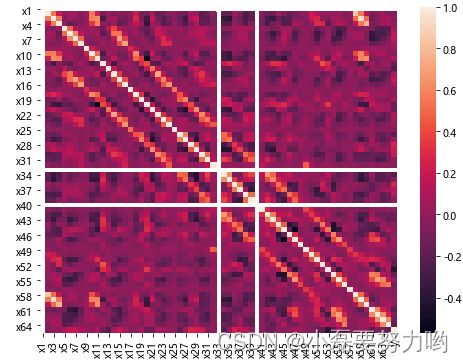
- 用于测量特征和因变量或特征间的线性相关性,结果相关系数的取值为[-1, 1],相关系数小于0代表两个特征负相关即反方向变化;相关系数大于0代表两个特征正相关即同方向变化;相关系数为0代表两者没有关系。相关系数的绝对值越大,说明两者的相关性越强。
pears = data.corr(method='pearson', min_periods=1) # 相关系数
plt.figure(figsize=(8,6))
sns.heatmap(pears) # 相关系数热力图
from sklearn.feature_selection import SelectKBest # 生成一个特征提取器
from sklearn.feature_selection import f_regression # 提取特征方法
selectKBest = SelectKBest(f_regression, k=4) # 生成一个利用相关系数法,提取4个特征的选择器
bestFeature = selectKBest.fit_transform(data.iloc[:,0:64], data[['y']]) # 拟合选取
selectKBest.get_support() # 输出bool值 提取出的特征为True
# 结果可以看出4个特征为:x13,x28,x36,x53 这四个特征与y值相关性较高
1.3、卡方检验
- 计算类别离散值之间的相关性。
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2 # 卡方检验
#选择K个最好的特征,返回选择特征后的数据
ch = SelectKBest(chi2, k=5) # 生成选择器:利用卡方检验保留5个特征
chh = ch.fit_transform(data.iloc[:,0:64],data['y'])
chh.shape,ch.get_support(),chh
# 5个特征为 x34,x35,x43,x44,x55
1.4、互信息法
- 互信息也是评价定性自变量对定性因变量的相关性的即离散型数值。
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import mutual_info_regression
m = SelectKBest(mutual_info_regression,k=5)
mm = m.fit_transform(data.iloc[:,0:64],data['y'])
mm.shape,m.get_support(),mm
# 5个特征为x27,x31,x34,x35,x43
2、Wrapper(包装法)
- 包装法的解决思路没有过滤法这么直接,它会选择一个目标函数来一步步的筛选特征。最常见的包装法就是递归特征消除法(recursive feature elimination),简称RFM法。
2.1、递归特征消除法
- 递归消除特征法使用一个基础机器学习模型来进行多轮训练,每轮训练后,消除若干权值系数的对应的特征,再基于新的特征集进行下一轮训练。在sklearn中,可以使用RFE函数来选择特征。基模型的特征是速度快,方便,但是效果可能不太好。
from sklearn.feature_selection import RFE
from sklearn.linear_model import LinearRegression
rfe = RFE(estimator = LinearRegression(), n_features_to_select=5)
RFE=rfe.fit_transform(data.iloc[:,0:64],data['y'])
RFE.shape,rfe.get_support(),RFE
3、Embedded(嵌入法)
- 嵌入法也是用机器学习的方法来选择特征,但是它和RFE的区别是它不是通过不停的筛掉特征来进行训练,而是使用的都是特征全集。最最常用的嵌入法包含基于惩罚项的特征选择法L1正则化和L2正则化,基于树模型的特征选择法决策树模型。
3.1、基于惩罚项的特征选择法
-
正则化是一种回归的形式,它将回归系数估计朝零的方向进行约束、调整或缩小。也就是说,正则化可以在学习过程中降低模型复杂度和不稳定程度,从而避免过拟合的危险。正则化包含L1和L2正则化。例如:下面的公式是岭回归的损失函数,,而后面加的就是L2正则惩罚项, α \alpha α是权衡系数。L1正则化则是加的 θ \theta θ的绝对值之和。
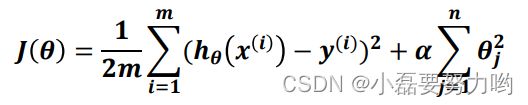
-
正则化惩罚项越大,那么模型的系数就会越小。当正则化惩罚项增大到一定程度时,所有的特征系数都会趋于0, 而其中一部分特征系数会更容易先变成0,这部分系数就是可以筛掉的。也就是说,我们选择特征系数较大的特征。
from sklearn.feature_selection import SelectFromModel # 从模型中选择就用这个模块
from sklearn.linear_model import LogisticRegression # 逻辑回归模型
s = SelectFromModel(LogisticRegression(penalty="l2", C=0.1)) # L2正则化 惩罚项系数为0.1
ss = s.fit_transform(data.iloc[:,0:64],data['y'])
ss.shape # (1797, 38) 保留了38个特征
- 关于正则化的讲解,可以看看这篇文章:
机器学习之线性回归(岭回归和Lasso回归)
3.2、基于树模型的特征选择
- 基于树的预测模型能够用来计算特征的重要程度,因此能用来去除不相关的特征。
from sklearn.feature_selection import SelectFromModel
from sklearn.ensemble import RandomForestRegressor # 随机森林回归器
s = SelectFromModel(RandomForestRegressor(n_estimators=20, max_depth=4)) # 20棵树即决策树,深度为4
ss = s.fit_transform(data.iloc[:,0:64],data['y'])
ss.shape # (1797, 13)
4、降维方法
看我之前的博客:机器学习之降维方法主成分分析与因子分析,详细介绍了PCA与因子分析的步骤原理及python如何实现降维的。
参考:
【机器学习】特征选择(Feature Selection)方法汇总
特征选择实践—python
《数据挖掘导论》[美] Michael Steinbach 著 范明 译