并查集相关题目“畅通工程”详细解析

并查集相关题目“畅通工程”详细解析

以下是一道有关“并查集”的题目

畅通工程
某省调查城镇交通状况，得到现有城镇道路统计表，表中列出了每条道路直接连通的城镇。省政府“畅通工程”的目标是使全省任何两个城镇间都可以实现交通（但不一定有直接的道路相连，只要互相间接通过道路可达即可）。问最少还需要建设多少条道路？

Input
测试输入包含若干测试用例。每个测试用例的第1行给出一个正整数和一个非负整数，分别是城镇数目N ( < 1000 )和道路数目M；随后的M行对应M条道路，每行给出一对正整数，分别是该条道路直接连通的两个城镇的编号。为简单起见，城镇从1到N编号。 注意:两个城市之间可以有多条道路相通,也就是说 3 3 1 2 1 2 2 1 这种输入也是合法的 当N为0时，输入结束，该用例不被处理。

Output
对每个测试用例，在1行里输出最少还需要建设的道路数目。
输入示例：

4 2
1 3
4 3
3 3
1 2
1 3
2 3
5 2
1 2
3 5
999 0
0

输出示例

1
0
2
998

题目中说

目标是使全省任何两个城镇间都可以实现交通（但不一定有直接的道路相连，只要互相间接通过道路可达即可）

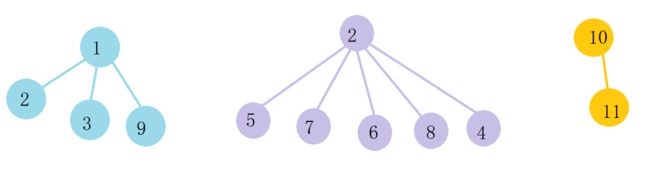
就以下面的图片为例：

意思是9和3这样的也算畅通，他们连在一起，在同一个整体中，但9和6就不连通，我们需要修路使他们连通。

蓝色的城市，紫色的城市，黄色的城市，分别都在一个整体（集合）中，同一个集合的城市都是互通的，所以我们很容易明白，要使所有城市连通，就需要把所有集合连通，集合与集合之间修一条路即可实现所有城市互通。

随后的M行对应M条道路，每行给出一对正整数，分别是该条道路直接连通的两个城镇的编号

那么在输入两条路连通之前，所有城市都是一个独立的集合,他们的父亲节点(parents[i])就是它们自己；

我们定义一个变量ans来表示集合的数量，最开始有多少个城市，就有多少个集合，因为ans和parents要在多个函数中使用，所以我们就把ans和parents定义为全局变量。

void Init(int n, int parents[1001])// 初始化
{
	for (int i = 0; i < n; i++)
	{
		parents[i] = i;
	}
	ans = n;
}

按照并查集的思想，我们是用里面元素的根节点来代表这个集合，所以，只要两个元素的根节点相同，那么我们就可以知道它们在一个集合，所以我们需要找元素的根节点。找到父亲的父亲直到找到根节点。

int findanc(int x)//找根+路径压缩
{
	return x == parents[x] ?  x :  (parents[x] = findanc(parents[x]));
}

这里我们还做到了路径压缩，即在找到元素根节点的同时，还把这个元素直接连到根节点上来，这样一来，下次就不需要找父亲的父亲的父亲去找这个元素的根节点，只需要一步就可以找到它的根节点。

输入两个城市的编号，也就是把这两个元素连在一起，也意味着它们属于同一个集合。

若5要和9连，只需把它们的根节点连在一起，即parents[findanc(a)] = findanc(b);//让5的根节点的父节点变为9的根节点，从而它们就连在一起了

void Union(int a, int b)//联合
{
	if (findanc(a) != findanc(b))//注意是在之前就没有联通过的情况下（如果之前连接过，那么它们就会在同一个集合，也就是它们的根就会一样）
	{
		parents[findanc(a)] = findanc(b);
		ans--;//两个集合每联合一次，集合就少一个
	}
}

最后需要修的路就是集合的数量减1，即ans-1；

整个代码如下：

#include
using namespace std;
int ans;
int parents[1001] = { 0 };
void Init(int n, int parents[1001])// 初始化
{
	for (int i = 0; i < n; i++)
	{
		parents[i] = i;
	}
	ans = n;
}
int findanc(int x)//找根+路径压缩
{
	return x == parents[x] ?  x :  (parents[x] = findanc(parents[x]));
}
void Union(int a, int b)//联合
{
	if (findanc(a) != findanc(b))//注意是在之前就没有联通过的情况下
	{
		parents[findanc(a)] = findanc(b);
		ans--;
	}
}
int main()
{
	int m, n;
	cin >> n;
	
	while (n)
	{
		cin >> m;
		Init(n, parents);
		for (int i = 0; i < m; i++)
		{
			int a, b;
			cin >> a>> b;
			Union(a, b);
		}
		cout << ans - 1 << endl;
		cin >> n;
	}
	return 0;
}

如果对你有帮助，别忘了点赞哦
如有疏漏，欢迎指正
我的主页还有其他内容，关注❤我，我们一起学习一起成长！