计算机组成原理_浮点数的定义

序言：
       博主个人认为本系列文章是目前博主看过的介绍“IEEE754”，即浮点数的机器存储的最好的文章。
       它比白中英老师的《计算机组成原理》，在大学时计算机相关专业一般会使用的“绿皮书”，更加通俗易懂，更加全面、更加深入，更有趣味。为了方便以后的学习，我将原知乎作者”李平笙“的五篇系列文章整理为了一篇。并对原文中存在的问题进行了勘误。在知乎上这个系列文章并不容易被搜索到，更不用提在全网上搜。本系列文章写的非常优秀，博主也希望让更多的人可以看到它，可以帮助更多的人学习和理解。因此，我整理并转发了本系列文章。
       我相信，只要你耐心按顺序阅读完本文，一定会对IEEE754以及编程语言中浮点数float、double有更深入的理解。说是理解IEEE754只看本文就够了，也不是看夸张。建议按照顺序阅读，加油：）
       作者说，这一系列文章其实是他在学习IEEE754标准的过程中, 总结的一系列笔记. 其中包含了一些个人理解, 所以如有偏差, 还望指出。整个系列大概会包含如下五部分：
一. 浮点数在内存中的存储方式
二. 浮点数的取值范围是如何计算的
三. 浮点数的精度是如何计算的
四. 非规格数, ±0, ±infinity和NaN都是什么
五. 浮点数的舍入规则(rounding

IEEE754标准: 一、浮点数在内存中的存储方式

1、什么是IEEE754标准

我们知道, 计算机内部实际上只能存储或识别二进制.

在计算机中, 我们日常所使用的文档, 图片, 数字等, 在储存时, 实际上都要以二进制的形式存放在内存或硬盘中, 内存或硬盘就好像是一个被划分为许多小格子的容器, 其中每个小格子都只能盛放0或1...

我们日常使用的 浮点数 也不例外, 最终也要被存储到这样的二进制小格子中.

这就涉及到了 应该怎么存 的问题, 比如, 对于浮点数 20.5, 是应该存储为 0100011 呢, 还是应该存储为 1100110 呢?

事实上直到20世纪80年代, 还是计算机厂商各自为战, 每家都在设计自己的浮点数存储规则, 彼此之间并不兼容. 直到1985年, IEEE754标准问世, 浮点数的存储问题才有了一个通用的工业标准.

IEEE754标准提供了如何在计算机内存中,以二进制的方式存储十进制浮点数的具体标准,

IEEE754标准发布于1985年. 包括 javascript, Java, C在内的许多编程语言在实现浮点数时, 都遵循IEEE754标准.

IEEE754的最新标准是IEEE754-2008, 但本篇文章主要参考的是IEEE754-1985, 好在两者相差并不大, 而参照1985的标准可以让我们对一些基础概念有更好的理解

IEEE754提供了四种精度规范, 其中最常用的是 单精度浮点型 和 双精度浮点型 , 但IEEE754并没有规定32位浮点数类型需要叫做 float, 或64位浮点数需要叫做 double. 它只是提供了一些关于如何存储不同精度浮点数的规范和标准. 不过一般情况下, 如果我们提到 float, 其实指的就是IEEE754标准中的32位单精度浮点数. 如果我们提到 double, 其实指的就是IEEE754标准中的64位双精度浮点数

下面是单精度浮点数和双精度浮点数的一些信息, 可以先简单看一下, 看不懂也没关系, 下文会对这里的信息做详细的解释...

单双精度浮点数对比

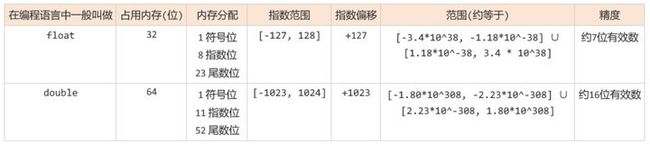
好啦, 铺垫完了, 开始正文吧~

2、32位单精度浮点数在内存中的存储方式

上文说到: IEEE754标准提供了如何在计算机内存中, 以二进制的方式存储十进制浮点数的具体标准, 并制定了四种精度规范.

这里我们主要研究 32位浮点数 (或者说单精度浮点数, 或者说float类型) 在计算机中是怎么存储的. 其他精度, 比如64位浮点数, 则大同小异.

想要存储一个32位浮点数, 比如20.5, 在内存或硬盘中要占用32个二进制位 (或者说32个小格子, 32个比特位)

这32个二进制位被划分为3部分, 用途各不相同:

32位浮点数内存占用示意图, 共使用了32个小格子

这32个二进制位的内存编号从高到低 (从31到0), 共包含如下几个部分:

sign: 符号位, 即图中蓝色的方块

biased exponent: 偏移后的指数位, 即图中绿色的方块

fraction: 尾数位, 即图中红色的方块

下面会依次介绍这三个部分的概念, 用途.

1. 符号位: sign

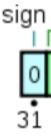
以32位单精度浮点数为例, 以下不再赘述:

符号位: 占据最高位(第31位)这一位, 用于表示这个浮点数是正数还是负数, 为0表示正数, 为1表示负数.

举例: 对于十进制数20.5, 存储在内存中时, 符号位应为0, 因为这是个正数

2. 偏移后的指数位: biased exponent

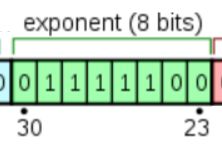
指数位占据第30位到第23位这8位. 也就是上图的绿色部分.

用于表示以2位底的指数. 至于这个指数的作用, 后文会详细讲解, 这里只需要知道: 8位二进制可以表示256种状态, IEEE754规定, 指数位用于表示[-127, 128]范围内的指数.

不过为了表示起来更方便, 浮点型的指数位都有一个固定的偏移量(bias), 用于使 指数 + 这个偏移量 = 一个非负整数. 这样指数位部分就不用为如何表示负数而担心了.

规定: 在32位单精度类型中, 这个偏移量是127. 在64位双精度类型中, 偏移量是1023. 所以, 这里的偏移量是127

⭐ 即, 如果你运算后得到的指数是 -127, 那么偏移后, 在指数位中就需要表示为: -127 + 127(偏移量) = 0

如果你运算后得到的指数是 -10, 那么偏移后, 在指数位中需要表示为: -10 + 127(偏移量) = 117

看, 有了偏移量, 指数位中始终都是一个非负整数.

看到这里, 可能会觉得还不是很清楚指数的作用到的是什么. 没关系, 让我们先继续往下看吧...

3. 尾数位:fraction

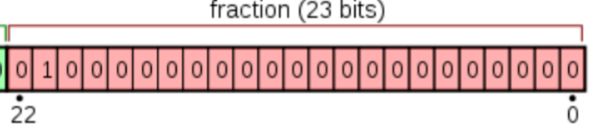
尾数位: 占据剩余的22位到0位这23位. 用于存储尾数.

在以二进制格式存储十进制浮点数时, 首先需要把十进制浮点数表示为二进制格式, 还拿十进制数20.5举例:

十进制浮点数20.5 = 二进制10100.1

然后, 需要把这个二进制数转换为以2为底的指数形式:

二进制10100.1 = 1.01001 * 2^4

注意转换时, 对于乘号左边, 加粗的那个二进制数1.01001, 需要把小数点放在左起第一位和第二位之间. 且第一位需要是个非0数. 这样表示好之后, 其中的1.01001就是尾数.

用 二进制数 表示 十进制浮点数 时, 表示为 尾数*指数的形式, 并把尾数的小数点放在第一位和第二位之间, 然后保证第一位数非0, 这个处理过程叫做 规范化(normalized)

我们再来看看规范化之后的这个数: 1.01001 * 2^4

其中1.01001是尾数, 而4就是偏移前的指数(unbiased exponent), 上文讲过, 32位单精度浮点数的偏移量(bias)为127, 所以这里加上偏移量之后, 得到的偏移后指数(biased exponent)就是 4 + 127 = 131, 131转换为二进制就是1000 0011

现在还需要对尾数做一些特殊处理

1. 隐藏高位1.

你会发现, 尾数部分的最高位始终为1. 比如这里的 1.01001, 这是因为前面说过, 规范化之后, 尾数中的小数点会位于左起第一位和第二位之间. 且第一位是个非0数. 而二进制中, 每一位可取值只有0或1, 如果第一位非0, 则第一位只能为1. 所以在存储尾数时, 可以省略前面的 1和小数点. 只记录尾数中小数点之后的部分, 这样就节约了一位内存. 所以这里只需记录剩余的尾数部分: 01001

所以, 以后再提到尾数, 如无特殊说明, 指的其实是隐藏了整数部分1. 之后, 剩下的小数部分

2. 低位补0

有时候尾数会不够填满尾数位(即图中的红色格子). 比如这里的, 尾数01001不够23位

此时, 需要在低位补零, 补齐23位.

之所以在低位补0, 是因为尾数中存储的本质上是二进制的小数部分, 所以如果想要在不影响原数值的情况下, 填满23位, 就需要在低位补零.

比如, 要把二进制数1.01在不改变原值的情况下填满八位内存, 写出来就应该是: 1.010 0000, 即需要在低位补0

同理, 本例中因为尾数部分存储的实际上是省略了整数部分 1. 之后, 剩余的小数部分, 所以这里补0时也需要在低位补0:

原尾数是: 01001(不到23位)

补零之后是: 0100 1000 0000 0000 000 (补至23位)

3、实例: 表示十进制浮点数20.5

在上面的讨论中, 我们已经得出, 十进制浮点数 20.5 的:

符号位是: 0

偏移后指数位是: 1000 0011

补零后尾数位是: 0100 1000 0000 0000 000

现在, 把这三部分按顺序放在32位浮点数容器中, 就是 0 1000 0011 0100 1000 0000 0000 000

这就在32位浮点数容器中, 以二进制表示了一个十进制数20.5的方式

这里有一个可以验证的IEEE754浮点数内存状态的网站, 我们来验证一下:

可见验证是通过的. 不过为了加深理解, 我们再反向推导一遍:

假设现在我们有一个用二进制表示的32位浮点数: 0 1000 0011 0100 1000 0000 0000 000, 求它所代表的十进制浮点数是多少?

观察可知:

符号位是0: 所以这是个正数.

尾数是: 0100 1000 0000 0000 000

去掉后面的补零, 再加上隐藏的整数部分1. 得到完整的尾数(含隐藏的整数部分)为: 1.01001

偏移后的指数位为: 1000 0011, 转换为十进制为131, 减去偏移量127, 得到真正的指数是 4

所以, 最后得到的浮点数 = 尾数(含隐藏的整数部分) * 以2为底的指数次幂

= 二进制的: 1.01001 * 2^4

= 把小数点向右移动4位

= 二进制的10100.1

= 十进制位20.5

注意, 直到最后一步才把二进制转换为十进制.

附带的, 这里还有一个进制转换网站, 可以看到二进制的10100.1, 确实等于十进制的20.5

到这里就讲解的差不多了,

随后是一张大体的计算方法示意图

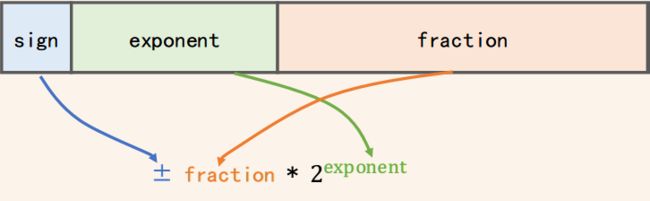
还有双精度类型的内存状态示意图:

存储双精度浮点数需要64个比特位. 其中最高位仍是符号位, 而指数位提升到了11位, 尾数位提升到了52位

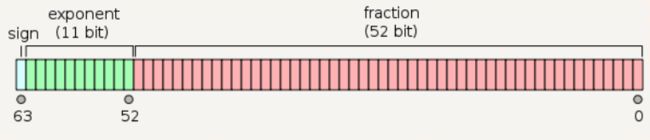
下一节会讲述为什么32位单精度浮点数的取值范围是

这个值究竟是如何计算出来的...

下一节再见吧~

IEEE754标准: 二, 32位浮点数的取值范围

这是"IEEE754标准系列"的第二段文章. 主要讨论32位浮点数 (或者说float类型) 的取值范围到底是如何计算出来的.

本章主要参考自

IEEE754 wiki​ en.wikipedia.org/wiki/IEEE_754-1985

1、wiki中, 32位浮点数的取值范围

这里先直接给出维基上的取值范围:

可见float类型, 或者说32位浮点数的取值范围是:

或者说是:

直观表示的话就是:

[-340000000000000000000000000000000000000, -0.0000000000000000000000000000000000000118] ∪ [0.0000000000000000000000000000000000000118, 340000000000000000000000000000000000000]

2、前置概念

在详细介绍这个范围是怎么计算出来的之前, 我们必须先了解一些概念.只有了解了这些概念, 才能真正的理解浮点数的取值范围是如何计算出来的.

而且此处假定你已经对IEEE754浮点数在内存中的存储方式有所了解, 还不了解的话也可以参考本系列的第一篇文章.

那这就开始吧

概念1: normal number(规格数) & subnormal number(非规格数)

根据IEEE754的规定, 按照尾数位隐藏的整数部分是 1. 还是0. 可以将浮点数划分为两类: normal number(规格数) 和 subnormal number(非规格数)

下面以32位浮点数为例来解释这些概念.

normal number(规格数)

就是尾数位隐藏的整数部分是1.的数, 这种数叫做normal number, 可以理解为"正常的数"

一般来说, 我们遇到的都是normal number

举例: 20.5在内存中表示为: 0 1000 0011 0100 1000 0000 0000 000

其中尾数部分(即上面的加粗部分), 去掉后面补的零之后为: 01001

但事实上, 真实的尾数部分应该是: 1.01001, 即前面省略了整数部分1.

subnormal number(非规格数)

尾数位隐藏的整数部分为0.的数, 叫做subnormal number, 也叫作denormal number, 可以理解为"低于正常数的数"

引入subnormal number这个概念, 是为了在浮点数下溢时, 可以逐位的损失精度, 以尽可能精确的表达0附近的极小数, 之后的章节会具体讲解.

为了表示subnormal number, IEEE754规定: 如果将指数位全部填充为0, 则表示这个数是个subnormal number

举例: 以32位浮点数为例, 当你看到类似于 * 00000000 *********************** 这样内存状态的数时, (即指数位全部为0的数), 就应该知道, 这是个subnormal number, 此时这个数的尾数位隐藏的整数不是1. 而是0.

概念2: non-number(特殊数)

和subnormal number类似, IEEE754对于指数位全为1的状态也做了特殊规定:

当指数位全部被1填充, 即指数位表示的值为255时, 用于表示这个浮点数处在一种非正常数(non-number)的状态: 即这个数可能是±infinity或NaN.

注: Infinity和NaN是两个特殊数, 分别表示无穷和Not a Number. 我们后文还会详细讨论这两个特殊数

The biased-exponent field is filled with all 1 bits to indicate either infinity or an invalid result of a computation.

所以: 当你看到类似于 * 11111111 *********************** 这样内存状态的数时, (即指数位全部为1的数), 就应该知道, 这是个non-number, 它用于表示特殊数.

3、计算方法

在了解了上面两个概念之后, 再看计算方法就很简单了.

如上所述, IEEE754规定, 当指数位全部为0或者全部为1时, 用于表示两种特殊状态的数: subnormal number 和 non-number, 所以现在可以得到如下示意图, 以32位单精度浮点数为例:

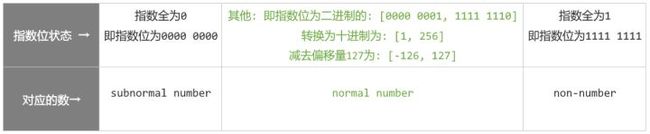
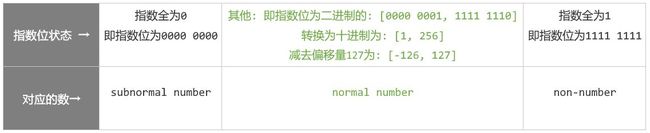
这就是理解单精度浮点数取值范围的关键: 当我们讨论浮点数的取值范围时, 实际上讨论的是: normal number (上图中绿色部分)的范围.

可以看出, 32位浮点数的指数部分其实是无法取到-127和128的, 因为:

用于表示-127的0000 0000被用来表示subnormal number了,

而用于表示128的1111 1111被用来表示non-number了.

所以实际上32位浮点数的指数部分只能取到只能取到[-126, 127]

再来看看尾数: 对于normal number, 尾数前隐藏的整数部分始终保持为1.

所以尾数(含隐藏的整数部分)所表示的值的范围其实是 [1.00...00, 1.11...11],

这个二进制数, 约等于十进制的[1, 2), 因为1.11..11非常逼近十进制的2

好啦, 现在我们知道, 对于32位flaot而言: 尾数(含隐藏的整数部分)的可取值为: [1 ,2), 指数位可取值[-126, 127], 且浮点数可正可负, 根据运算规则, 就不难算出32位float的取值范围了:

取值范围

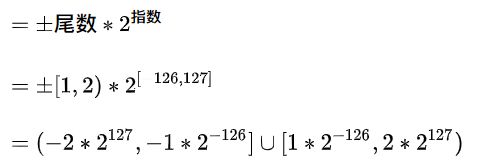
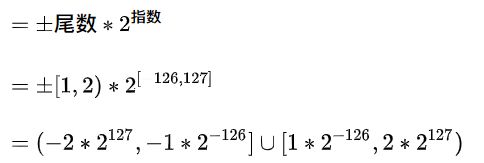
注意开闭区间哦

然后为了看着顺眼, 我们把上式的以2为底, 替换为以10为底:

↑ 转换后小数位太长了, 所以这里写成了省略号的形式: 3.402823669...

从上面这个集合中, 取一个更容易表示的子集, 就是我们常见的32位float的取值范围了:

↑ 注意, 上面这个集合其实是32位float取值范围的子集, 不过和真正的取值范围也没有差太多, 表示起来也更简洁, 没有冗长的小数位, 还能写成闭区间的形式...所以在各种资料中, 我们常看到的取值范围就是上面这个.

↑ 之所以能写成闭区间的形式, 就是因为它只是真正取值范围的一个子集. 这里特意说明一下, 防止有的同学对这里的闭区间感到困惑.

4、补充

下面是 32位单精度浮点数的取值范围示意图, 可以参照此图更好的理解一下前文内容

下图中, x轴代表以2为底的n次幂(即内存中的指数部分), y轴代表尾数(含隐藏的整数部分1.)

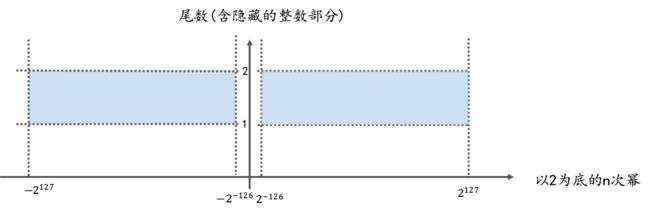
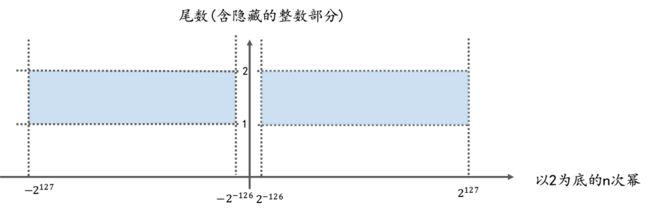
坐标系中任意一点(x, y)就代表一个浮点数,

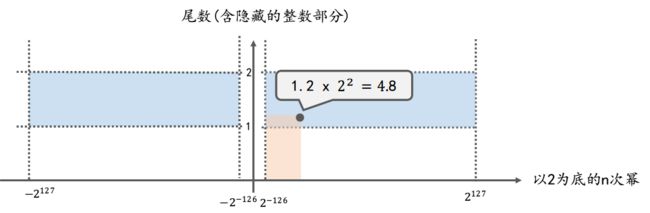
这一点到x轴, y轴所围成的矩形的面积(即上图中橙色区域的面积), 就是这个浮点数的值 (即浮点数的值 = 尾数(含隐藏的整数部分) * 以2为底的n次幂)

上图中:

蓝色部分: 表示normal number的取值范围, 即, normal number类型的浮点数对应的坐标点只能出现在坐标系中的蓝色区域.

坐标点: 一个坐标点对应一个浮点数

橙色部分的面积: 表示该浮点数的值.

这就是32位浮点数取值范围的计算方法.

下一章将详细介绍为什么说32位浮点数的精度是"7位有效数", 这个7是怎么计算出来的, 下一章也将会是整个系列中最有难度, 最重要的一章.

那下一章再见吧~

IEEE754标准: 三、为什么说32位浮点数的精度是"7位有效数"

️️本章包含一些自己的理解, 如有偏差还望指出. 本章也是整个系列最重要的一章, 请耐心阅读。

关于IEEE754标准中浮点数的精度是怎么计算的, 网上的资料众说纷纭, 有些还彼此冲突, 我也看的很头大……这里仅分享两种个人觉得比较靠谱的说法。

1、先说结论

打开IEEE754的维基百科，可以看到其中标注着, 单精度浮点数的精度是"Approximately 7 decimal digits"

有人把这句话翻译为 "大约7位小数" , 把"decimal"翻译成了"小数".

但个人理解, 这里 "decimal的" 含义应该是 "十进制的" , 即32位浮点数的精度是 "大约7位十进制数" , 后文会说为什么这样理解.

2、在讨论之前…

我们先来思考这样一件事: 现在的计算机能存储[1,2]之间的所有小数吗?

稍想一下就知道: 不可以. 因为计算机的内存或硬盘容量是有限的, 而1到2之间小数的个数是无限的.

极端一点, 计算机甚至无法存储1到2之间的某一个小数, 比如对于小数 1.00000.....一万亿个零.....00001, 恐怕很难用计算机去存储它...

不过计算机却能存储[1, 10000]之间的所有整数. 因为整数是"离散"的, [1, 10000]之间的整数只有10000个. 10000种状态, 很容易就能存储到计算机中, 而且还能进行运算, 比如计算10000 + 10000, 也只是要求你的计算机能存储20000种状态而已...

这样来看的话: 计算机可以进行数学概念中的整数运算的, 但却难以进行数学概念中的小数运算. 小数这种"连续"的东西, 当前的计算机很难应对...

事实上, 计算机为了进行小数运算, 不得不将小数也当成"离散"的值, 一个一个的, 就像整数那样:

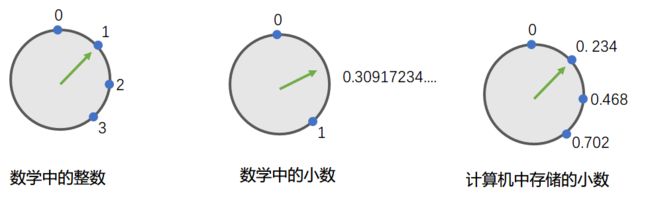
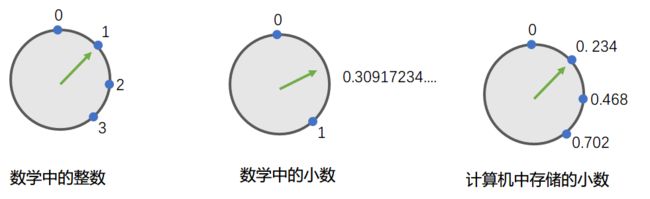
↑ 数学中的整数是一个一个的, 想象绿色指针必须一次走一格

↑ 数学中的小数是连续的, 想象绿色指针可以无极调节, 想走到哪儿走到哪儿

↑ 计算机中存储的小数是一个一个的, 绿色指针必须一次走一格, 就像整数那样

这就引发了精度的问题, 比如上图中, 我们无法在计算机中存储0.3, 因为绿色指针只能一次走一格, 要么在0.234, 要么就到了0.468...

当然, 我们也可以增加计算机存储小数的精度, 或者说缩小点与点之间的间隔:

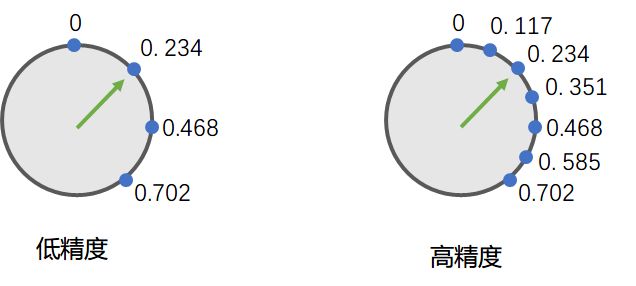
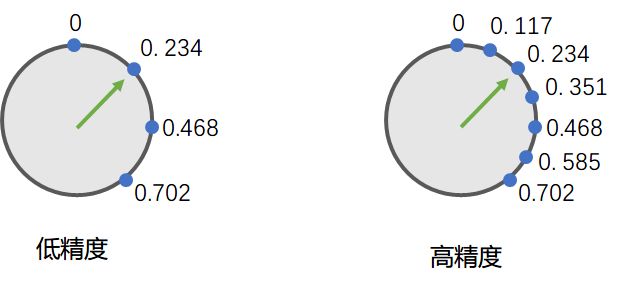
IEEE754中的单精度浮点数和双精度浮点数大体也是如此: 双精度浮点数中的蓝色小点更密集...

3、理解角度1: 从"间隔"的角度理解

1. 铺垫

从"间隔"的角度理解来"精度", 其实是这样一种思路:

想象一个类似于上图的圆形表盘, 表盘上有一些蓝点作为刻度, 有一个绿色的指针用于指向蓝点, 绿色指针只能一次走一格: 即只能从当前蓝点移动到下一个蓝点. 不能指向两个蓝点之间的位置.

假如表盘上用于表示刻度的蓝点如下所示:

0.0000

0.0012

0.0024

0.0036

0.0048

0.0060

0.0072

0.0084

0.0096

0.0108

0.0120 (注意这里, 前一个数是108, 这个数是120, 先记住这一点)

0.0132

0.0144

...

即, 这是一组十进制数, 这组数以 0.0012 的步长逐渐递增... 假设这个表盘就就是你的计算机所能表示的所有小数.

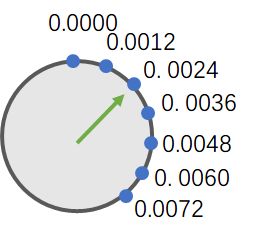表盘示意图

问: 我们能说这个表盘, 或者说这组数的精度达到了 4 位十进制数吗(比如, 可以精确到1位整数 + 3位小数)?

分析: 如果说可以精确点1位整数 + 3位小数, 那我们就应该可以说出下面这样的话:

我们可以说, 当前指针正位于0.001x: 而指针确实可以位于0.0012, 属于0.001x (x表示这一位是任意数, 或说这对该位的精度不做限制)

我们可以说, 当前指针位于0.002x: 而指针确实可以位于0.0024, 属于0.002x

我们可以说, 当前指针位于0.003x: 而指针确实可以位于0.0036, 属于0.003x

...

我们可以说, 当前指针位于0.009x: 而指针确实可以位于0.0096, 属于0.009x

我们可以说, 当前指针位于0.010x: 而指针确实可以位于0.0108, 属于0.010x

我们可以说: 当前指针位于0.011x...但, 注意, 指针始终无法指向0.011x...在我们的表盘中, 指针可以指向0.0108, 或指向0.0120, 但始终无法指向0.011x

...

这就意味着: 对于当前表盘 (或者说对于这组数) 来说, 4位精度太高了...4位精度所能描述的状态中, 有一些是无法用这个表盘表示的.

那, 把精度降低一些.

我们能说这个表盘, 或者说这组数的精度达到了 3 位十进制数吗(比如, 可以精确到1位整数 + 2位小数)?

再来分析一下: 如果说可以精确点1位整数 + 2位小数, 那我们就应该可以说出下面这样的话:

我们可以说, 当前指针位于0.00xx: 而指针确实可以位于0.0012, 0.0024, 0.0036...0.0098, 这些都属于0.00xx

我们可以说, 当前指针位于0.01xx: 而指针确实可以位于0.0108, 0.0120...这些都属于0.01xx

...

可以看出, 对于当前这个表盘 (或者说对于这组数) 来说, 它完全能"hold住"3位精度. 或者说3位精度所能描述的所有状态在该表盘中都可以得到表示.

如果我们的机器使用这个表盘作为浮点数的取值表盘的话, 那我们就可以说:

我们机器的浮点数精度 (或者说这个表盘的浮点数精度), 能精确到3位十进制数(无法精确到4位十进制数).

而这个精度, 本质上是由表盘间隔决定的, 本例中的表盘间隔是0.0012, 如果把表盘间隔缩小到0.00000012, 那相应的表盘能表示的精度就会提升(能提升到 7 位十进制数, 无法达到 8 位十进制数)

通过这个例子, 希望大家能够直观的认识到 "表盘的间隔" 和 "表盘的精度" 之间, 存在着密切的关系. 这将是后文进行讨论的基础.

事实上: ieee754标准中的32位浮点数, 也可以被想象为一个 "蓝点十分密集的浮点数表盘", 如果我们能分析出这个表盘中蓝点之间的间隔, 那我们就能分析出这个表盘的精度.

注: 也可以用一句很简单的话来解释本小节的例子: 假设浮点数表盘能提供4位精度控制, 比如能控制到1位整数+3位小数, 这就要求它必须能控制到 0.001 这个粒度, 而 0.001 这个值小于该表盘的实际间隔 0.0012... 所以该表盘不能提供4位精度...

2. 32位浮点数的间隔

那怎么分析32位浮点数的间隔与精度呢, 有一个很笨的方法: 把32位浮点数能表示的所有小数都罗列出来, 计算间隔. 然后分析精度...

呃...我也确实准备用这个比较笨的方法...下面就开始吧...

注: 此处只分析规格数(normal number), 且先不考虑负数情况, 也就是说不考虑符号位为 1 的情况

32位浮点数能表示的最小规格数是 :

0 00000001 00000000000000000000000 (二进制)

(注意, 规格数的指数位最小为 00000001 , 不能为00000000. 这个在本系列的第二章中已经讨论过了, 以下不再赘述)

紧邻的下一个数是:

0 00000001 00000000000000000000001 (二进制)

紧邻的下一个数是:

0 00000001 00000000000000000000010 (二进制)

紧邻的下一个数是:

0 00000001 00000000000000000000011(二进制)

...

这样一步一步的往下走, 步之后, 我们将指向这个数:

0 00000001 11111111111111111111111(二进制)

再走一步, 也就是2^23步之后, 我们将指向这个数:

0 00000010 00000000000000000000000(二进制)

总结一下: 2^23次移动之后:

我们从起点: 0 00000001 00000000000000000000000,

移动到了终点: 0 00000010 00000000000000000000000

现在可以求间隔了, 间隔 = 差值 / 移动次数 = (终点对应的值 - 起点对应的值) / 2^23,

但是, 先别急着计算. 我们先仔细观察一下, 可以发现, 和起点相比, 终点的符号位和尾数位都没变, 仅仅是指数位变了: 起点指数位00000001 → 终点指数位00000010, 终点的指数位, 比起点的指数位变大了1

而ieee754中浮点数的求值公式是:

(先不考虑符号位)

这样的话: 假如说起点对应的值是

那终点对应的值就应该是

即, 仅仅是指数位变大了1

把指数展开会看的更清晰一些:

假如说起点对应的值是 0.0000 0001 (8位小数)

那终点对应的值就应该是 0.0000 001 (7位小数)

那起点和终点的差值就是: (0.0000 001 - 0.0000 0001), 是一个非常小的数

那间隔就是: 差值 / 2^23

注意: 其实上面我们并没有计算出真正的间隔, 只是假设了起点和终点的值分别是

和

然后算出了一个假设的间隔. 但这个假设格外重要, 下文我们会继续沿用这个假设进行分析 ️

废话不多说, 现在我们继续前进.

现在起点变成了: 0 00000010 00000000000000000000000

再走2^23步, 来到了: 0 00000011 00000000000000000000000

同样: 符号位, 尾数位都没有变, 指数位又变大了1

沿用上面的假设, 此时起点对应的值是

, 则终点对应的值应该是

, 即, 还是指数位变大了1

再次计算差值: 0.0000 01(6位小数) - 0.0000 001(7位小数)

再次计算间隔: 等于 差值 / 2^23(移动次数)

不知道同学们有没有体会到不对劲的地方, 没有的话, 我们计算往前走:

现在起点变成了: 0 00000011 00000000000000000000000

再走2^23步, 来到了: 0 00000100 00000000000000000000000

同理, 终点相对起点, 还只是指数位变大了1

再次计算差值: (0.00001(5位小数) - 0.000001(6位小数))...

再次计算间隔: 等于 差值 / 2^23(移动次数)

感受到不对劲了吗? 继续往前走...

现在起点变成了: 0 00000100 00000000000000000000000

再走2^23步, 来到了: 0 00000101 00000000000000000000000

再次计算差值: (0.0001(4位小数) - 0.00001(5位小数))...

再次计算间隔: 等于 差值 / 2^23(移动次数)

...一路走到这儿, 感受到不对劲了吗?

不对劲的地方在于: 终点和起点的差值! 差值在越变越大! 同理间隔也在越变越大!

不信的话我们来罗列一下之前的差值:

...
那差值就是: 0.0000 001 ( 7位小数) - 0.0000 0001( 8位小数), 差值等于0.0000 0009
...
那差值就是: (0.000001 ( 6位小数) - 0.0000001( 7位小数)), 差值等于0.0000 009
...
那差值就是: (0.00001 ( 5位小数) - 0.000001( 6位小数)), 等于 0.0000 09
...
那差值就是: (0.0001 ( 4位小数) - 0.00001( 5位小数)), 等于 0.0000 9

差值的小数点在不断向右移动, 这样走下次, 总有一天, 差值会变成9, 变成90, 变成90000...

而 移动次数始终 = 2^23, 间隔始终 = 差值/2^23....差值在越变越大, 间隔也会跟着越变越大...

到这里, 你发现了ieee754标准的一个重要特性: 如果把ieee754所表示的浮点数想象成一个表盘的话, 那表盘上的蓝点不是均匀分布的, 而是越来间隔越大, 越来越稀疏:

大概就像这样:

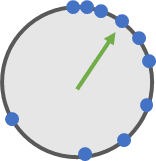
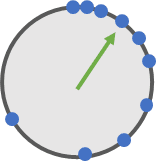
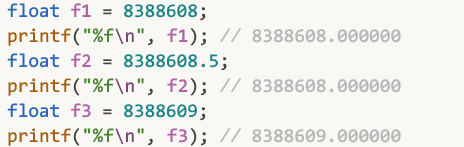
你可以直接在c语言中验证这一特性:

与16777216紧邻的蓝点是16777218, 两数差值为2, 32位浮点数无法表示出16777217

3. 32位浮点数的间隔表

开头我们说过: 知道了表盘的间隔, 就能计算表盘的精度了.

复杂的地方在于, ieee754这个表盘, 间隔不是固定的, 而是越来越大.

幸运的地方在于, wiki已经帮我们总结好了间隔数据:

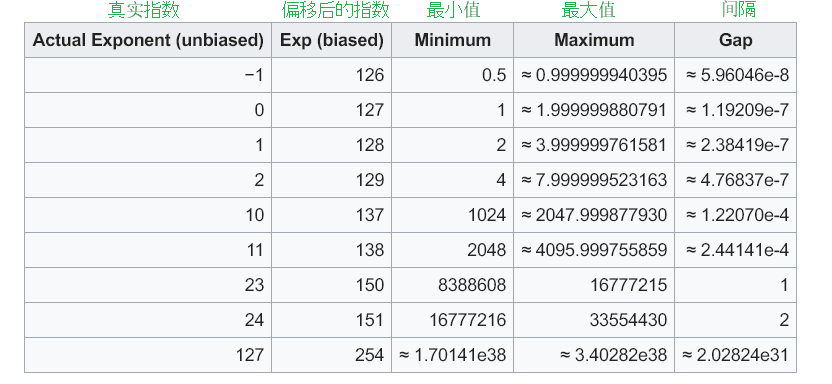
对于这张表的数据, 我们只关注右侧的三列即可, 它是在告诉我们: [最小值, 最大值]范围间的间隔是多少

比如: 下面这一行告诉我们, 8388608 ~ 16777215这个范围之间的数, 间隔是1

所以32位浮点数可以存储8388608, 也可以存储8388609, 但无法存储8388608.5, 因为间隔是1

而第二行在说: 1 ~ 1.999999880791这个范围之间的数, 间隔是: 1.19209e-7

去翻一下c语言float.h的源码, 会发现这样一句:

#define FLT_EPSILON 1.192092896e-07F // smallest such that 1.0+FLT_EPSILON != 1.0

↑ 定义常量FLT_EPSILON, 其值为1.192092896e-07F

这个 1.192092896e-07F , 其实就是我们表格中看到的间隔: 1.19209e-7

源码中说: 32位浮点数1.0, 最少也要加上FLT_EPSILON这个常量, 才能不等于1.0.

换句话说, 如果 1.0 加上一个小于 FLT_EPSILON 的数 N, 就会出现1.0 + N == 1.0 这种"诡异的情况".

因为对于 1 ~ 1.999999880791 这个范围中的32位浮点数, 至少要加上 FLT_EPSILON, 或者说至少要加上该范围对应的间隔, 才能够把指针从当前蓝点, 移动到紧邻的下一个蓝点

注意: 如果不是1 ~ 1.999999880791之间的数, 则不一定要加上 1.19209e-7 啊. 准确来说应该是: 某个区间中的数, 至少要加上该区间对应的间隔, 才能从当前蓝点移动到下一个蓝点.

仔细看一看一下上面那张间隔表, 相对你对c语言的浮点数运算会更胸有成竹.

注意: 其实上面的解释中, 存在着一个不大不小的问题. 不过这里先搁置不谈, 等我们理解的更深刻一些时, 再拐回来重新探讨这个问题.

注: 64位浮点数的 间隔表, 也可以参见 IEEE754 WIKI

4. 32位浮点数的精度

那, 为什么说32位浮点数的精度是7位十进制数呢?

首先要说明的是: 32位浮点数的精度是: Approximately 7 decimal digits, 是大约7位十进制数

事实上, 对于有些8位十进制数, 32位浮点数容器也能对其精确保存, 比如, 下面两个数都能精确保存

那所谓的精度是7位十进制数到底是什么意思呢? 探讨这个之前, 我们需要先了解一些更本质的东西

I. 浮点数只能存储蓝点位置对应的值

正如前文所说, 32位浮点数会形成一个表盘, 表盘上的蓝点逐渐稀疏. 绿色指针只能指向某个蓝点, 不能指向两个蓝点之间的位置. 或者换句话说: 32位浮点数只能保存蓝点对应的值.

如果你要保存的值不是蓝点对应的值, 就会被自动舍入到离该数最近的蓝点对应的值. 举例:

在0.5 ~ 1这个范围内, 间隔约为5.96046e-8, 即约为 0.00000005.96046

也就是说: 表盘上有一个蓝点是0.5

下一个蓝点应该是: 当前蓝点 + 间隔 ≈ 0.5 + 0.00000005.96046 ≈ 0.5000000596046

那, 如果我们要保存 0.50000006, 也就是我们要保存的这个值, 稍大于下一个蓝点:

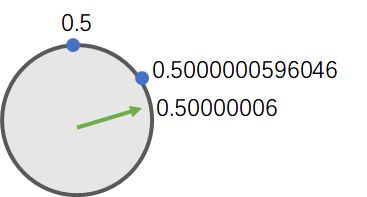
因为绿色指针必须指向蓝点, 不能指向蓝点之间的位置, 所以绿色指针会被"校准"到0.5000000596046, 或者说我们要保存的0.50000006, 会被舍入为0.5000000596046

实测一下:

事实上, 每个32位浮点数容器中, 存储的必然是一个蓝点值

验证一下, 首先求出从0.5开始的蓝点值:

第一个蓝点: 0.5

第二个蓝点: ≈ 0.5 + 0.0000000596046 ≈ 0.5000000596046

第三个蓝点: 第二个蓝点 + 0.0000000596046 ≈ 0.0000001192092

第四个蓝点: 第三个蓝点 + 0.0000000596046 ≈ 0.0000001788138

然后看下面的代码, 发现变量中实际存储的, 其实都是蓝点值:

看打印出来的东西, 可以发现实际存储的都是蓝点值

这是我们需要着重理解的东西

说句题外话, 其实学到现在, 我们就能大体解释一个经典编程问题了: "为什么32位浮点数中的 0.99999999 会被存储为1.0呢", 因为 0.99999999 不是一个蓝点值, 且离他最近的蓝点值是1.0, 然后绿色指针被自动"校准"到了离他最近的蓝点1.0.

II. 理解32位浮点数的精度是7位十进制数

对此我是这样理解的:

例1:

查表, 发现 1024 ~ 2048 范围中的 间隔 约为 0.000122070

如下图: 想要精确存储到小数点后4位, 却发现做不到, 其实只能精确存储到小数点后3位:

试图精确存储到小数点后4位, 却发现实际上无法存储1024.0005, 因为表盘上没有这个1024.0005xxxxxxxx这个级别的数

在这个1024 ~2048这个范围内, 能精确保存的数是 4位十进制整数 + 3位十进制小数 = 7位十进制数

例2:

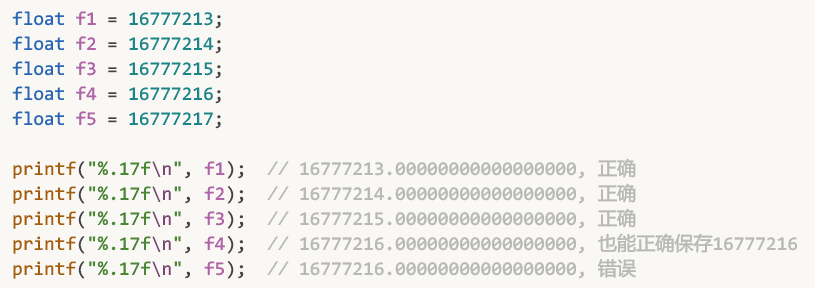
查表, 发现 8388608 ~ 16777215 范围中的 间隔 为 1

如下图: 想要精确存储到小数点后一位, 却发现做不到, 其实只能精确存储到小数点后零位, 或者说只能精确存储到个位数(因为最小间隔为1):

小数点后一位无法精确存储, 只能精确存储到个位

在这个8388608 ~ 16777215 这个范围内, 能精确保存的数是 7或8位十进制整数 + 0位十进制小数 = 7或8位十进制数

是的, 32位浮点数也能精确保存小于等于 16777215 的 8 位十进制数, 所以说其精度大约是7位十进制数

例3:

查表, 发现 1 ~ 2 范围中的间隔为 1.19209e-7

如下图: 想要精确存储到小数点后7位, 却发现做不到, 其实只能精确存储到小数点后6位:

想精确存储到小数点后7位, 却发现实际上无法存储1.0000012, 表盘上没有这个1.0000012xxxx 这个级别的数

在这个1 ~ 2这个范围内, 能精确保存的数是 1位十进制整数 + 6位十进制小数 = 7位十进制数

所谓的32位浮点数的精度是7位十进制数, 大概就是这样算出来的. 基本上 整数位 + 小数位 最多只能有7位, 再多加无法确保精度了 (注意这不是wiki给出的计算方法, wiki给出的算法见下文)

如果你不喜欢这种理解方式, 不妨退一步, 仅记住如下三点即可:

1. 32位浮点数其实只能存储对应表盘上的蓝点值

而不能存储蓝点与蓝点之间的值

2. 蓝点不是均匀分布的, 而是越来越稀疏. 或者说蓝点与蓝点之间的间隔越来越大, 或者说精度越来越低.

这也是为什么到1.xxxxxxx时还能精确到小数点后6位, 到http://1024.xxx时只能精确到小数点后3位, 到8388608 时只能精确到个位数的原因. 因为蓝点越来越稀疏了, 再往后连个位数都精确不到了...

5. 注意事项

I. 区分32位浮点数的存储精度 & 打印效果

在c语言中, 使用 %f 打印时, 默认打印 6 位小数

32位浮点数的有效位数是 7 位有效数

这两者并不冲突, 比如:

原始值 1234.878 89

打印效果 1234.878 906

可见打印效果中只有 前7位 和 原始值 是一致的

事实上, "原始值" vs "打印出来的值" , 其实就是 "你想要存储的值" vs "实际存储的值"

你想要存储1234.878 89, 但实际存储的是1234.878 906... 因为1234.878 906...才是个"蓝点值", 才能真正的被绿色指针所指向, 才能真正的被32位浮点数容器所存储.

虽然不能精确存储你想要保存的值, 但32位浮点数能保证精确存储你想要保存的值的前 7 位. 所以打印效果中的前7位和 原始值 是一致的.

%f 默认打印到6位小数, 打印出来的是实际存储的蓝点值. 但, 蓝点值可不一定是7位小数, 可能有十几位小数, 只是 %f 会默默的将其舍入为7位小数并打印出来

II. 有时候精度不是7位

可能的原因有很多, 比如:

1. 打印时, %f发生了舍入:

此时可以设置打印更多的小数位

2. 好像精确度不止7位

注意, 浮点数中能存储的都其实是蓝点值

所以, 如果 你要存储的值 和 蓝点值 完全一样, 那你要存储的值就能够被完全精确的存储下来的.

如果 你要存储的值 和 蓝点值 非常非常靠近, 就会体现出超乎寻常的精度. 详见下例:

3. 好像精确度不到7位

举例:

对此, 个人理解是:

对于 1024 ~ 2048之间的数, 32位浮点数确实有能力精确到7位有效数

当你要存储的值不是一个蓝点值时, 会发生舍入, 自动舍入到离它最近的一个蓝点值

所以, 1024.001, 会舍入到离它最近的蓝点1024.000976..., 体现的好像精度不足7位

而1024.0011, 就会舍入到离它最近的蓝点1024.00109..., 体现的好像精度又足7位了...

只是说: 32位浮点数确实有精确到7位有效数的能力, 但舍入规则使得它有时好像无法精确到7位...

从这个角度去理解的话, 前面我们讨论过的一个话题就有点站不住脚了:

前面我们说过: :

c语言的float.h中有这样一行代码:
#define FLT_EPSILON 1.192092896e-07F // smallest such that 1.0+FLT_EPSILON != 1.0
↑ 定义常量 FLT_EPSILON, 其值为 1.192092896e-07F
这个 1.192092896e-07F , 其实就是我们1 ~ 2范围中的 间隔: 1.19209e-7
源码中说: 32位浮点数 1.0, 最少也要加上 FLT_EPSILON这个常量, 才能 不等于1.0
换句话说, 如果 1.0 加上一个 小于 FLT_EPSILON 的数 N, 就会出现 1.0 + N == 1.0 这种"诡异的情况".

等等, 这里好像忽略掉了舍入规则: 1 ~ 2范围中, 两个蓝点之间的间隔是: 1.19209e-7, 但这并不意味着想从当前蓝点走到下一个蓝点需要走满一个间隔啊, 因为有舍入规则的存在, 其实你只要走大半个间隔就行了, 然后舍入规则会自动把你舍入到下一个蓝点...

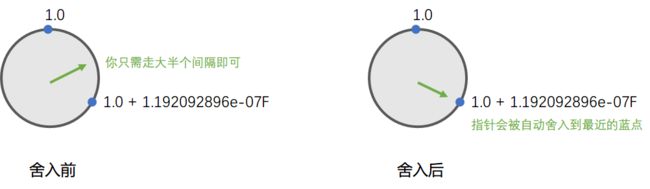
在c语言中验证一下:

测试环境: win10 1909, gcc version 6.3.0 (MinGW.org GCC-6.3.0-1)

可见, 因为有舍入机制的存在, 一个蓝点想移动到下一个蓝点: 大体上只需移动间隔的一半多一点即可.

而c语言中的这行注释:

#define FLT_EPSILON 1.192092896e-07F // smallest such that 1.0+FLT_EPSILON != 1.0

其实也不太对, 1.0 也不需要加上 FLT_EPSILON 这一整个间隔才能 != 1.0 (或者说才能到下一个蓝点), 大体上只需加上 FLT_EPSILON的一半多一点 就能 !=1.0 了(或者说就能到下一个蓝点了).

不过这也只是个人理解...

III. 0.xxxxxxx 到底能精确到小数点后几位

或者说, 32位浮点数能记录7位有效数, 那对于 0.xxxxxxx 这种格式的数, 到底是能精确到小数点后7位, 还是小数点后6位. 或者说, 此时整数部分的0算不算有效数...

个人理解, 对于0.xxxxxxx这也的小数, 其实能精确到小数点后7位, 即0不算一位有效数

以0.5 ~ 1这个范围为例, 此时的间隔是间隔是5.96046e-8, 约等于0.0000 0006

下面尝试精确到小数点后8位, 发现不行.

但精确到小数点后7位确是绰绰有余:

而0 ~ 0.5之间, 间隔则会更小, 精度则会更高 (因为浮点数表盘上的蓝点是越来越稀疏, 精度越来越差的. 如果靠后的0.5 ~ 1范围中能精确到小数点后7位, 那更靠前的0 ~ 0.5中只会更精确, 或者说蓝点只会更密集, 间隔只会更小)

举例:

总之还是那就话: 大体来说, 32位浮点数的精度是7位有效数.

事实上, 浮点数中只能存储蓝点, 蓝点越靠近0就越密集, 精度就越高. ←7位有效数是对这一现象的总结和概括性描述

最后说一点: 有些同学可能会错误的认为32位浮点数类型的精度是: 始终能精确到小数点后6位, 比如能精确存储999999.123456, 但不能精确存储999999.1234567

相信读到这里, 大家都能找出这种理解的错误之处了: 32位浮点数的精确度是7位有效数, 大体来说, 这7位有效数, 指的是 整数 + 小数一共7位, 而不是说始终能精确到小数点后六位...

IV. 深入理解间隔表

我们再回头看看这张wiki上的间隔表. 其实它主要就是在告诉我们: 某个范围中, 两个蓝点间的间隔是多少.

比如在1 ~ 2范围中, 两个蓝点间的间隔约是1.19209e-7

在 8388608 ~ 16777215范围中, 两个蓝点间的间隔是1

这里其实有几个注意事项:

1. 每个范围中, 都有2^32个蓝点, 或者每个区间都被等分为2^23个间隔

比如范围1~2会被等分为2^23个间隔, 范围 8388608 ~ 16777215 也会被等分为2^23个间隔

2. 范围的划分由指数决定

所谓的范围1~2会被等分为2^23个间隔, 准确来说应该是范围2^0 ~ 2^1会被等分为2^23个间隔

所谓的范围8388608 ~ 16777215会被等分为2^23个间隔, 准确来说应该是范围2^23 ~ 2^24会被等分为2^23个间隔

每次指数位变更, 都会划分出新的范围. 这其实很好理解:

比如, 现在我们位于起点: 0 00000010 00000000000000000000000

往前移动2^23 - 1步, 或者说往前移动2^23 - 1个间隔, 对应的其实就是把尾数从00000000000000000000000, 一步步变成11111111111111111111111

再往前走一步, 也就是共往前移动了2^23个间隔, 我们来到了终点: 0 00000011 00000000000000000000000

可见终点相对起点, 仅指数位增长了1

终点到起点, 就确定了一段范围. 该范围被等分成了2^23个间隔. (终点 - 起点) / 2^23就是每个间隔的长度.

再往前走2^23个间隔, 就来到了0 00000100 00000000000000000000000, 同样是指数变大了1...

这就不难看出: 指数位的变更用于划分范围, 尾数位的变更用于往前一步步移动.

有多少个尾数位, 决定了每个范围中可以划分出多少个间隔, 比如有23个尾数位, 就意味着每个范围中可以划分出2^23个间隔

有多少指数位, 决定我们可以囊括多少的范围. 比如有8个指数位 (可表示的指数范围是[-127, 128]), 那我们的范围划分就是这样的:

2^-127 ~ 2^-126是一个范围

2^-126 ~ 2^-125是一个范围

...

2^0 ~ 2^1 是一个范围

2^1 ~ 2^2 是一个范围

...

2^127 ~ 2^128 是一个范围

上面每个范围都会被尾数位等分为2^23份间隔

增大指数位不会增大精度: 比如, 如果将指数位增大到16位(可表示的指数范围是[-32767, 32768]), 那我们的范围划分是这样的

2^-32767 ~ 2^-32766是一个范围

2^-32766 ~ 2^-32765是一个范围

...

2^-127 ~ 2^-126是一个范围

2^-126 ~ 2^-125是一个范围

...

2^0 ~ 2^1 是一个范围

2^1 ~ 2^2 是一个范围

...

2^32767 ~ 2^32768是一个范围

上面每个范围依旧会被尾数位等分为2^23份间隔

注意: 2^0 ~ 2^1, 这个范围还是被等分为2^23份间隔, 2^-126 ~ 2^-125, 这个范围还是被等分为2^23份间隔...

每个范围的精度都没有任何提升.

增大尾数位才会增大精度: 比如, 将尾数位增大为48. 则每个范围会被等分为2^48份间隔. 这样每个范围中的间隔才会变小, 蓝点才会变密集, 精度才会提升.

总结: 指数位的多少控制着能囊括多少个范围, 尾数位的多少控制着每个范围的精度, 或者说控制着每个范围中间隔的大小, 蓝点的密度.

希望这能让你对ieee754标准中的指数位, 尾数位的 具体作用, 控制什么 有更好的理解.

4. 理解角度2: WIKI中的计算方法

理解角度2倒是相当简单.

我们说过, 32位浮点数在内存中是这样表示的: 1位符号位, 8位指数位, 23位尾数位

事实上尾数位是24位, 因为在尾数位前还隐藏了一个整数部分1. 或 0. (可以参见本系列的第一篇文章)

仔细想一下, 浮点数内存的三个部分中:

符号位: 用于控制正负号

指数位: 控制指数, 其实也就是控制小数点的移动:

就好像在十进制中:

1.2345e2 = 123.45

1.2345e3 = 1234.5, 指数位+1只是把小数点向后移动了一位. 二进制中也是一样的, 指数位也仅仅用于控制小数点的移动. 比如0.01 → 0.001 (小数点向左移动了一位)

尾数位: 其实真正控制精度的, 或者说真正记录状态的, 只有尾数位.

在24位尾数中

从: 0.0000 0000 0000 0000 0000 000

到: 0.0000 0000 0000 0000 0000 001

...

一直到: 1.1111 1111 1111 1111 1111 111

共包含2^24种状态, 或者说能精确记录2^24种不同的状态:

0.0000 0000 0000 0000 0000 000 是一种状态,

0.0000 0000 0000 0000 0000 001 又是一种状态,

1.0010 1100 0100 1000 0000 000 又是另一种状态

...

如果你准备记录2^24 + 1种状态, 那尾数就不够用了. 或者说就不能满足你对精度的需求了.

在这种视角下: 精度 和 可表示的状态数 之间画上了等号.

总结一下: 32位浮点数一共能记录2^24种状态 (符号位用于控制正负, 指数位用于控制小数点的位置. 只有尾数位用于精确记录状态)

对于 float f = xxx; 其中xxx是个数值, 不管xxx你是用什么进制书写, 只要是使用32位浮点数作为容器, 就最多只能精确记录2^24种状态, 就好像一个32位浮点数大楼中一共有2^24个房间一样.

事实上, xxx我们一般用10进制书写,

而2^24 = 16 777 216(十进制), 即32位浮点数容器最多只能存储16 777 216(十进制)种状态

16 777 216 是个8位数

所以32位浮点数的精度最多是7位十进制(0 - 9 999 999), 共10 000 000种状态

如果32位浮点数的精度是8位十进制的话(0 - 99 999 999), 这一共是100 000 000种状态, 大于了32位浮点数能存储的状态上限16 777 216...所以说精度到不了8位十进制数.

到这里就分析完毕了.

如果你更喜欢数学表达式的话, 那么 "32位浮点数的精度最多是N位十进制" , N是这样算出来的:

下面是wiki中对该算法的描述:

The number of decimal digits precision is calculated via number_of_mantissa_bits * Log10(2). Thus ~7.2 and ~15.9 for single and double precision respectively.

如wiki中所说, 32位浮点数的精度大约是7位十进制数, 64位浮点数的大约是16位十进制数.

注: 对于这两种理解角度: 理解角度2更简单一些, 可以直接用数学公式计算出精度. 理解角度1(也就是从间隔的角度去理解)的解释性更强一些, 细节更丰富, 能解释的现象也更多一些.

5.总结

本章大体总结了 "32位浮点数的精度是7位十进制数" 的两种计算方法. 关于这一话题, 网上的资料比较混乱, 所以这里加入了一些自己的理解. 如有错误还望指出.

下一章会讲解一下IEEE754标准中的一些非规格数与特殊数, 包括 ±0, ±INFINITY, 和NaN

IEEE754标准: 四、非规格数, ±infinity, NaN

第一章提到过, ieee754标准中, 浮点数包含三种状态

1. normal number(规格数)

2. subnormal number(非规格数)

3. non-number(特殊数)

本章详细讲解这三种状态.

1、首先, 如何区分这三种状态

其实这三种状态是通过指数部分区分的, 而且很容易区分.

以32位浮点数为例, 其内存状态分为3部分:

1位符号位 8位指数位 23位尾数位

其中, 如果8位指数位全为0, 就代表当前数是个非规格数. 或者说, 形如 * 00000000 *********************** 格式的数就是非规格数.

如果8位指数位全为1, 就代表当前数是个特殊数. 或者说, 形如 * 11111111 *********************** 格式的数就是特殊数.

如果8位指数不全为0, 也不全为1(也就是除去以上两种状态外, 剩下的所有状态), 这个数就是规格数.

随便几个例子: * 10101100 ***********************就是一个规格数

可见: 非规格数和特殊数是两种特殊状态, 规格数则是非常常见的状态

示意图:

注意下图把特殊数分为了两种状态, 无穷大和NaN:

深入理解计算机系统第三版

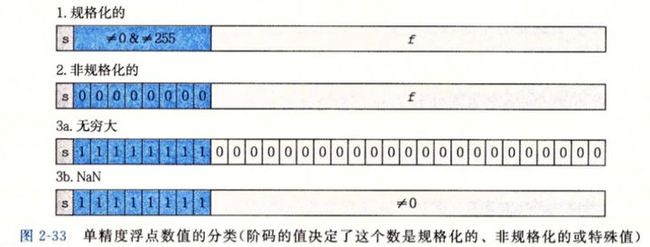
2、 这三种状态的作用

为什么要把浮点数分为这三种状态呢? 答案当然是有用啊, 而且作用相当直观:

规格数: 用于表示最常见的数值, 比如1.2, 34567, 7.996, 0.2. 但规格数不能表示0和非常靠近0的数.

非规格数: 用于表示0, 以及非常靠近0的数, 比如1E-38.

特殊数: 用于表示"无穷"和"NaN":

浮点数的存储和计算中会涉及到"无穷"这个概念, 比如:

32位浮点数的取值范围是

如果你要往里面存储4e38(这超过了最大的可取值), 32位浮点数就会在内存中这样记录 "你存储的数超过了我的最大表示范围, 那我就记录你存储了一个无穷大..."

浮点数的存储和计算中还会涉及到"NaN (not a number)"这个概念, 比如:

你要给一个负数开根号(如 √-1), 但是ieee754标准中的浮点数却不知道该怎么进行这个运算, 它就会在内存中这样记录 "不知道怎么算, 这不是个数值, 记录为NaN"

可见, 这三种状态都是非常有用的, 作用也非常直观, 下面我们一个个来讲.

3、状态1: 规格数

对于规格数:

符号位, 1位: 可正可负

指数位, 8位: 不全为0, 且不全为1

对于32位浮点数来说, 规格数的指数位的取值范围是[1, 254], 偏置bias是127, 所以实际的指数是:

[1 - 127, 254 - 127], 即 [-126, 127]

注: 关于偏置, 可参见本系列第一章, 此处不再赘述

尾数位, 23位: 尾数位前隐藏的整数部分是1. 而非 0.

所以尾数位的取值范围是[1.00000000000000000000000, 1.11111111111111111111111] (二进制)

换算为10进制为[1,2)

注: 关于尾数位前隐藏的数, 可参见本系列第一章, 此处不再赘述

规格数的局限性: 无法表示 0 和 及其靠近0 的数

原因很简单, ieee754浮点数的求值公式是:

所以可求出32位浮点数的取值范围就是:

问题就出现在这里:

注意尾数部分: 取值范围是[1, 2), 始终大于1

注意指数部分:

这个数始终大于0, 即便2^-167非常小, 但还是大于0

那么: 一个始终大于1的数 * 一个始终大于0的数, 永远无法等于0

事实上, 1(尾数最小值) * 2^-167(指数最小值) = 2^-167. 2^-167就是当前我们能表示的最小值

也就是说: 使用规格数时, 我们除了无法表示0, 也无法表示(0, 2^-167)之间的, 靠近0的极小数...

这就是规格数的局限性, 这个局限性将由非规格数解决.

补充一点:

其实在本系列的第二章, 我们计算过32位浮点数的取值范围:

所以这里可以画一个示意图:

↑ 绿色区域就是32位浮点数中规格数的取值范围, 可见它取不到0和靠近0的极小数

↑ 红色区域包含0和靠近0的极小数, 红色区域其实是非规格数的取值范围, 见下一节.

4、状态2: 非规格数

对于非规格数:

符号位, 1位: 可正可负

指数位, 8位: 全为0

对于32位浮点数来说, 规格数的指数位全为0, 对应的值也是0. 偏置bias依旧是127, 但:

实际指数的计算方法是: 实际指数 = 1 - bias = 1 - 127 = -126, 即非规格数的实际指数固定为-126. 注意这是规定.

其实我们可以发现, 非规格数实际指数的计算方法(实际指数 = 1 - bias), 和规格数实际指数的计算方法(实际指数 = 指数位的值 - bias)不同

后文会看到这样规定的原因.

尾数位, 23位: 尾数位前隐藏的整数部分是0. 而非 1.

所以尾数位的取值范围是[0.00000000000000000000000, 0.11111111111111111111111] (二进制)

换算为10进制为[0,1)

非规格数的作用: 表示0和靠近0的数

那么规格数是怎么完成这个任务的呢.

首先看看非规格数是怎么表示0的:

依旧要用到我们的ieee754浮点数求值公式:

然后, 非规格数尾数的取值范围是[0, 1), 指数固定为-126. 这就很简单了, 让尾数取0不就能表示数值0了:

可见当尾数取0时, 通过变更符号位, 我们可以表示出+0和-0, IEEE754规范中也确实存在着这两种表示0的方式

注: 某些场景下, +0和-0会被认为完全相同, 某些场景下, +0和-0又被认为不完全相同. 这往往取决于具体的编程语言和应用场景, 此处不做讨论. 只需知道IEEE754中可以表示+0和-0即可. +0和-0在IEEE754中是两种内存状态(符号位不同)

然后看看非规格数是怎么表示接近0的数的:

准确来说, 我们要看看, 对于32位浮点数, 非规格数是怎么表示出

之间的数的. 也就是如何表示出下图中的红色区域的:

其实也很简单:

浮点数求值公式:

然后, 非规格数尾数的取值范围是[0, 1), 指数固定为-126.

所以, 非规格数的取值范围就是:

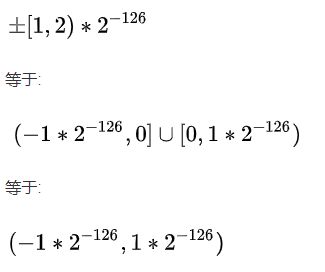
这样就完成了...

现在我们尝试着把32位浮点数中的非规格数的取值范围, 和规格数的取值范围拼接在一起

32位浮点数中, 非规格数的取值范围:

32位浮点数中, 规格数的取值范围:

仔细看一下, 啊...非规格数的取值范围, 正好可以卡在规格数取值范围的中间, 现在我们得到了一个完整的取值范围:

感觉世界一下子清爽了起来.

这就是非规格数的作用: 用于表示0和靠近0的数, 用于和规格数"珠联璧合", 形成一个完整的取值范围.

不过这还没有完...

5、非规格数补充

1. 逐渐溢出

前文说过, 非规格数尾数的取值范围是[0, 1), 指数固定为-126

所以是尾数的变化在导致非规格数的值变大, 举例:

0 00000000 00000000000000000000001

就比

0 00000000 00000000000000000000000

要大一些

随着尾数逐渐增大, 相应的非规格数也在不断增大:

...

0 00000000 11111111111111111111111 这是非规格数的最大值

此时尾数(带上隐藏的整数部分0.)其实是0.11111111111111111111111, 是个比1小一点点的数, 不妨记做(1 - ε)

那, 此时非规格数的值就是

好, 我们再往前前进一格, 此时会进入规格数的范围:

0 00000001 00000000000000000000000

这是个规格数,

其尾数位的值: 其实隐藏了 1. 或者说, 此时真正的尾数应该是1.00000000000000000000000 , 也就是1

其指数位的值: 是1, 则实际指数应该是1 - bias = 1-127 = -126

所以这个规格数的值就是:

, 这是规格数的最小值.

注意到没有: 非规格数的最大值是:

规格数的最小值是:

两者之间实现了非常平滑的过度, 非规格数的最大值非常紧密的连接上了规格数的最小值

非规格数 "一点点逐渐变大, 最后其最大值平稳的衔接上规格数的最小值", 这种特性在ieee754中被叫做逐渐溢出(gradual underflow)

明白了这一点, 就很容易想通:

① 为什么规定非规格数的尾数前隐藏的整数部分是 0. 而规格数尾数前隐藏的整数部分是1.

② 为什么非规格数的真实指数的计算公式是 1 - bias, 而规格数的真实指数的计算公式是 指数部分的值 - bias 了

仔细思考一下, 就是这些设计实现了逐渐溢出这种特性.

↑ 关于第①点: 这使得非规格数的尾数取值范围是[0,1), 而规格数的尾数取值范围是[1,2), 两者平滑的衔接在了一起

↑ 关于第②点: 这使得对于32位浮点数来说, 非规格数的真实指数固定为-126, 而规格数的指数是[-126, 127], 两者也平滑的衔接在了一起...

2. 密集分布

第三章中我们说过: 如果把ieee754浮点数想象成一个表盘的话, 那表盘上的蓝点是越来越稀疏的. 或者说越靠近0越密集.

不过当时仅讨论了规格数的分布情况, 那非规格数呢.

答案是, 非规格数的蓝点分布间隔, 和规格数中蓝点最密集的区域(也就是最靠近0的区域)一致, 可以验证一下:

非规格数: 范围是

在这个范围中分布了2^23个蓝点, 则蓝点间的间隔是

规格数中蓝点最密集的区域, 也就是最靠近0的区域是:

, 在这个范围中分布了2^23个蓝点, 则蓝点间的间隔是

所以, 即便把非规格数与规格数放在一起审视, ieee754浮点数表盘上的蓝点依旧是越靠近0越密集, 越靠近∞越稀疏

深入理解计算机系统第三版, 浮点数密度示意图. 中间部分密密麻麻的都是非规格数

下面是在c语言中的测试结果:

6、状态3: 特殊数

特殊数分为两种: 无穷和NaN

1. 先说无穷

理解了非规格数, 再理解无穷就很简单了, 两者有很多相似之处:

对于无穷:

符号位, 1位: 可正可负

指数位, 8位: 全为1

尾数位, 23位: 全部为0

当内存位于上述状态时, 就表示无穷(infinity)

具体写出来就是: * 11111111 00000000000000000000000 用于表示无穷(infinity)

其中符号位可正可负, 分别记做+infinity和-infinity

以32位浮点数为例, 其规格数的取值范围是:

当要存储的数大于规格数取值范围的最大值时, 就会被记做+infinity, 比如2^128, 刚刚超过规格数的取值范围的最大值, 就会被记做+infinity

当要存储的数小于规格数取值范围的最小值时, 就会被记做-infinity, 比如-2^128, 刚刚小于规格数的取值范围的最小值, 就会被记做-infinity

需要注意的是: 所有+infinity的内存状态都是0 11111111 00000000000000000000000, 不会有任何变动

2^128对应的内存状态是0 11111111 00000000000000000000000

2^123456789对应的内存状态还是0 11111111 00000000000000000000000

同理, -infinity的内存状态都是1 11111111 00000000000000000000000

此外: 就像非规格数的最大值可以和规格数的最小值平稳衔接一样, 规格数的最大值也可以和+infinity平稳衔接:

规格数的最大值是: 0 11111110 11111111111111111111111

尾数位其实是1.11111111111111111111111, 非常接近2, 不妨记做2-ε

指数是127

所以最大值是:

+infinity的内存状态则是: 0 11111111 00000000000000000000000

尾数其实是: 1.00000000000000000000000, 等于1

指数是128

所以+infinity的内存状态对应的值是:

可见规格数的最大值也能和+infinity平稳衔接. -infinity同理.

现在我们就集齐了整个数轴:

↑ 而且各个节点都能平稳的衔接在一起

2. NaN

NaN则更简单, 前面说过, 如果计算出来的值不是一个数值, 则记录为NaN

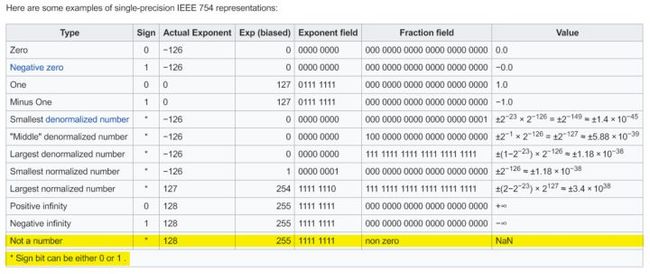
NaN的内存状态是:

符号位, 1位: 可正可负

指数位, 8位: 全为1

尾数位, 23位: 不全为0即可

仅仅是一种特殊状态标记而已.

需要注意的是, 根据wiki, 没有+NaN或-NaN这种说法, 统称为NaN

7、总结

本章介绍了IEEE754规范中的非规格数, 特殊值(±infinity, NaN), 包括它们的内存状态, 作用, 工作原理等.

下一章会先偏离一下主线, 补充一些之前没有提到的琐碎知识点.

下一章再见吧~

IEEE 754标准: 五、一些补充

本章讨论一些零碎的话题.

1、其他导致浮点数存储不精确的原因

在第三章中我们提到过, 数学中的小数是连续的, 而计算机中的小数(准确来说是ieee754标准中的小数)是离散的.

这就会引发精度问题: 图中的绿色指针只能指向蓝点, 不能指向蓝点之间的数. 比如上面最右边的图, 绿色指针其实无法指向0.3, 当你想要指向0.3时, 实际上会被舍入为0.234, 即舍入到离它最近的蓝点对应的值.

而除此之外, 进制问题也会导致IEEE754浮点数存储不精确

简单来说就是: 有限长度编码下, 每种进制都有他们不能精确表示的值

比如: 10进制不能精确的表示1/3 (0.3333333.....)

十进制可以精确表示1/5 (0.2), 但二进制无法精确表示1/5

不能精确表示时，只能进行近似. 编码长度越长，近似程度越高

举例: 下图尝试用二进制表示0.2, 可以发现, 只能近似表示...

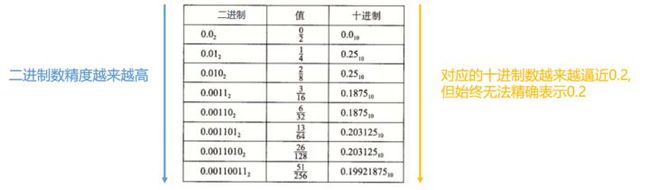
当你把一个十进制数存储到计算机中时, 实际上存储的是该数的二进制表示.

所以, 当你写入如下代码时:

float f = 0.2;

虽然0.2(十进制)远远没有到达32位浮点数的精度上限(7位精度), 但计算机其实无法精确地存储该数值, 因为0.2(十进制)无法使用二进制格式精确表示.

此时变量f对应的内存状态是这样的:

↑ 你键入的是0.2

↑ 内存中实际存储的是0.20000000298023223876953125

可以在c语言中验证一下:

可见十进制的0.2无法用二进制精确表示, 但十进制的0.5却可以用二进制精确表示.

2、二进制的小数形式

有些同学可能会纳闷, 二进制为什么会有小数形式? 我常见的二进制都是整数形式啊, 比如十进制的9, 表示为二进制是1001, 怎么会有 1001.101 这种二进制的小数格式呢.

其实对于程序员来说, 这里确实比如容易让人困惑, 比如win10自带的计算机, 就不支持二进制小数:

二进制模式下, 小数点是不能用的

许多编程语言, 比如js, 也不支持直接使用二进制小数:

支持二进制整数, 但不支持二进制小数

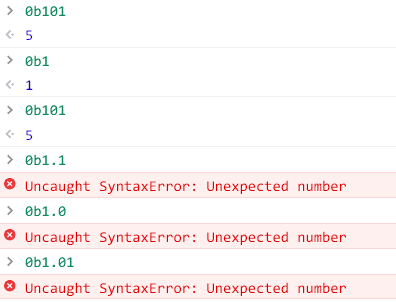
但和十进制一样, 二进制其实也有小数形式, 而且很容易理解:

比如对于十进制数 78.23

十位: 7, 表示

个位: 8, 表示

十分位: 2, 表示2/10, 或说表示

百分位: 3, 表示3/100, 或说表示

这个十进制所表示的值是: 70 + 8 + 2/10 + 3/100

二进制数也是同理的:

比如对于二进制数 10.11

第一位: 1, 表示1 * 2^1 = 2

第二位: 0, 表示0 * 2^0 = 0

第三位: 1, 表示1 * 2^-1 = 0.5

第四位: 1, 表示1 * 2^-2 = 0.25

所以这个二进制表示的值, 其实就是十进制的2 + 0 + 0.5 + 0.25 = 2.75

这里比较有意思的一点是:

十进制小数点后面的那一位(也就是十分位), 对应的权是1/10, 也就是0.1

即, 对于十进制数3.4, 这个4对应的值是: 4 * 权 = 4 * 0.1 = 0.4

而二进制小数点后面的一位, 对应的权是1/2, 也就是十进制的0.5

所以对于二进制数0.1, 这个1对应的值是: 1 * 0.5 = 0.5, 所以二进制的0.1, 其实等于十进制的0.5

这让我想起来一个脑筋急转弯, 问: 什么时候 0.1 比 0.2 要大?

答: 当0.1是个二进制数, 而0.2是个十进制数的时候...

事实上: 对于小数点之后的位, 二进制的位权始终比十进制的位权要大, 举例:

十进制数: 小数点之后的位权依次是: 1/10, 1/100, 1/1000...

二进制数: 小数点之后的位权依次是: 1/2, 1/4, 1/8... 相应位的权始终比↑十进制的要大

所以会出现这种现象

二进制: 1.000001, 小数点后面的数看起来已经很小很小了

对应的十进制是: 1.015625, 小数点后面的数其实还挺大...

在IEEE765标准中, 我们会经常和二进制小数打交道, 所以这里补充一下相关知识.

3、关于32位浮点数, 一些不太正确的认知

1. 32位浮点数能存储很大的整数

这是32位浮点数的取值范围:

当我第一次看到这个取值范围时, 我是很惊讶的, 怎么这么大?

一个浮点数, 占用32字节, 竟然能存储下约±340000000000000000000000000000000000000这么大的数

相比之下, 一个同样32字节的long类型, 存储范围只有约±2147483647

那我为啥还要用long类型...

...

一路学习到现在, 倒是可以绕过这个弯儿了, 那就是:

32位浮点型确实最大可以存储到

这么大的数, 但精度很低

第三章中我们说过, 32位浮点数表盘中的蓝点会越来越稀疏:

等到了

这么大的数时, 其实蓝点已经稀疏的不成样子了, 基本是不可用状态

根据wiki中给出的间隔, 对于1.70141e38 到 3.40282e38范围中的数, 间隔是2.02824e31

也就是说, 大体上: 32位浮点数中, 能精确存储1.70141e38

但无法精确存储1.70141e38 + 1

也无法精确存储1.70141e38 + 2,

也无法精确存储1.70141e38 + 100000000000

...

下一个能精确存储的数是: 1.70141e38 + 20282400000000000000000000000000 (即加上间隔)

这个精度基本上是不可用的.

事实上, 如果你要用float存储整数的话, 最多只能精确存储到 16777216

再大的话, 间隔就会变为2, 就不适合用来存储整数了:

此时再回过头来看看同为 32位 的long类型, 能精确存储的整数范围

约是: ±2147483647

比: ±16777216 大多了

所以存储大整数还是用long类型吧

总结: 32位浮点数只是有能力存储到

, 实际上存储的数过大会导致精度过低, 基本上不可用. 用32位浮点数存储整数时, 只适用存储±16777216之间的整数.

2. 32位浮点数能存储很精确的小数

这是32位浮点数的取值范围:

看起来好像能存储

这么精确的小数...

但其实和存储整数一样, 32位浮点数只是有能力存储到

这么小的小数而已...

事实上在第三章中我们详细讲解过: 32位浮点数的精确度是7位有效数.

即如果你要存储的数 整数部分 + 小数部分 放在一起超过了 7 位, 32位浮点数就不能精确存储了

比如, 32位浮点数就不能精确存储我们常背的部分圆周率

32位浮点数倒是可以存储常见的月工资, 比如 5078.65, 或 12665.73. 但如果要存储年工资, 或把工资存储到3位小数, 32位浮点数就不一定够用了...

所以, 虽然32位浮点数的取值范围看起来很大, 足足有:

但其实32位浮点数只适合存储常见数据...

感性地去认知的话, float(也就是32位浮点数)类型其实和int类型有些相似: int用于存储最常用, 最自然的整数. float则用于存储最常用, 最自然的浮点数...编程时, 如果要存储的数很大或精度很高(相对来说，这些数往往不怎么常用或不怎么自然), 就要考虑改用long或double.

精确来说的话, 就是不要被32位浮点数骇人的取值范围吓到. 而是记住事实上它只能存储7位有效数就行了.