矩阵【线性代数系列（二）】

矩阵【线性代数系列（二）】

꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ

꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ

---

1.线性方程组

对有n个未知数和m个方程的线性方程组：

      $a_{11}{x}_1+a_{12}{x}_2+...+a_{1n}{x}_n=b_1$
      $a_{21}{x}_1+a_{22}{x}_2+...+a_{2n}{x}_n=b_2$
      $...$
      $a_{m1}{x}_1+a_{m2}{x}_2+...+a_{mn}{x}_n=b_m$

当$b_1,b_2,...,b_m$不全为0时，线性方程组被称为n元非齐次线性方程组。

当$b_1,b_2,...,b_m$全为0时，线性方程组被称为n元齐次线性方程组。

对n元齐次线性方程组，$x_1,x_2,...x_n=0$一定是它的解，这个解叫做n元齐次线性方程组的零解。
n元齐次线性方程组一定有零解，但不一定有非零解。

---

2.矩阵的概念

m×n个数字组成的m行n列矩阵：
$$\left[\begin{array}{cccc}{a}_{11}& a_{12}& ...& a_{1n}\\ a_{21}& a_{22}& ...& a_{2n}\\ ...& ...& ...& ...\\ a_{m1}& a_{m2}& ...& a_{mn}\end{array}\right]$$
被称为m×n矩阵。
当m=n时也被称为$n阶矩阵$或n阶方阵。
如果A和B是行数和列数都相同的矩阵，则称A与B是同型矩阵。
如果同型矩阵A和B对应位置的元素都相等，则称A与B相等。
元素都是实数的矩阵称为实矩阵，元素都是复数的矩阵称为复矩阵。
只有一行的矩阵称为 行矩阵，也称 行向量。
只有一列的矩阵称为 列矩阵，也称 列向量。
元素都是0的矩阵是$零矩阵$，可简记为$o$
对非齐次线性方程组：

      $a_{11}{x}_1+a_{12}{x}_2+...+a_{1n}{x}_n=b_1$
      $a_{21}{x}_1+a_{22}{x}_2+...+a_{2n}{x}_n=b_2$
      $...$
      $a_{m1}{x}_1+a_{m2}{x}_2+...+a_{mn}{x}_n=b_m$

可以表示为矩阵：
$$\left[\begin{array}{cccc}{a}_{11}& a_{12}& ...& a_{1n}\\ a_{21}& a_{22}& ...& a_{2n}\\ ...& ...& ...& ...\\ a_{m1}& a_{m2}& ...& a_{mn}\end{array}\right]\times \left[\begin{array}{c}{x}_1\\ x_2\\ ...\\ x_n\end{array}\right]=\left[\begin{array}{c}{b}_1\\ b_2\\ ...\\ b_n\end{array}\right]$$

其中，
第一个矩阵是 系数矩阵，第二个矩阵是 未知数矩阵，第三个矩阵是 常数项矩阵。

---

也可以写成
$$\left[\begin{array}{ccccc}{a}_{11}& a_{12}& ...& a_{1n}& b_1\\ a_{21}& a_{22}& ...& a_{2n}& b_2\\ ...& ...& ...& ...& ...\\ a_{m1}& a_{m2}& ...& a_{mn}& b_n\end{array}\right]\times \left[\begin{array}{c}{x}_1\\ x_2\\ ...\\ x_n\\ 1\end{array}\right]=\left[\begin{array}{c}0\\ 0\\ ...\\ 0\end{array}\right]$$

这种形式下，第一个矩阵被称为 增广矩阵。

---

3. 对角矩阵 与 单位矩阵

$$\Lambda =\left[\begin{array}{cccc}{\lambda }_1& 0& ...& 0\\ 0& {\lambda }_2& ...& 0\\ ...& ...& ...& ...\\ 0& 0& ...& {\lambda }_n\end{array}\right]$$
像这样，从左上，到右下角直线上以外的元素都为0的矩阵，被称为 对角矩阵。简称 对角阵。对角阵也记作
 
            $\Lambda =diag({\lambda }_1,{\lambda }_2,...,{\lambda }_n)$

---

特别的，当${\lambda }_1={\lambda }_2=...={\lambda }_n=1$时，矩阵如下：
$$E=\left[\begin{array}{cccc}1& 0& ...& 0\\ 0& 1& ...& 0\\ ...& ...& & ...\\ 0& 0& ...& 1\end{array}\right]$$
这样的矩阵叫做 单位矩阵，简称单位阵。
 
单位矩阵的元可以表示为：
$$e_{ij}=\{\begin{array}{rlr}1& ,& 当i=j\\ 0& ,& 当i\ne j\end{array}(i,j=1,2,...,n)$$

---

4.矩阵的运算

4.1 矩阵的加法

两个同型矩阵可以相加，相加方式为对应位置的数字之间相加。
矩阵的加法是满足交换律的。

---

4.2 矩阵的数乘

数量乘法（数乘）
使用一个常数乘以一个矩阵，即使用该常数乘以矩阵中的每一个元素。
矩阵的数乘满足乘法的交换律和结合律，以及分配率。

---

4.3 矩阵的乘法

以$C=AB$为例，则A、B需要满足A的列数等于B的行数。设A是m×s矩阵，B是s×n矩阵，则C是一个m×n矩阵。则
     $c_{ij}={\sum }_{k=1}^s{a}_{ik}{b}_{kj}=a_{i1}{b}_{1j}+a_{i2}{b}_{2j}+...+a_{is}{b}_{sj}$

矩阵的乘法不满足交换律。但是满足结合律和分配率。

---

为了方便记忆，这里引入实际情景，
 
以多元回归方程的矩阵形式为例：
其中，对$X_{ij}$，不同的 $i$ 表示不同的特征，不同的j表述不同的样本。
即$X_{ij}$所在的矩阵的第一列是为引入常数项准备的，后边每一列对应一个特征，而每一行表示一个样本，$\beta 1$表示截距项，$\beta 2$~$\beta k$则表示每个特征的回归系数，${\mu }_i$表示残差项。$x_{ij}$所在的矩阵与${\beta }_i$所在的矩阵相乘，得到的是一个n行1列的矩阵，即与${\beta }_i$所在的矩阵有着相同的shape。
$$\begin{array}{c}\left[\begin{array}{c}{Y}_1\\ Y_2\\ ...\\ Y_n\end{array}\right]=\left[\begin{array}{ccccc}1& X_{21}& X_{31}& ...& X_{k1}\\ 1& X_{22}& X_{32}& ...& X_{k2}\\ ...& ...& ...& ...& ...\\ 1& X_{2n}& X_n& ...& X_{kn}\end{array}\right]\left[\begin{array}{c}{\beta }_1\\ {\beta }_2\\ ...\\ {\beta }_k\end{array}\right]+\left[\begin{array}{c}{u}_1\\ u_2\\ ...\\ u_n\end{array}\right]\end{array}$$
$$=\begin{array}{c}\left[\begin{array}{c}1\times {\beta }_1+X_{21}{\beta }_2+X_{31}{\beta }_3+...+X_{k1}{\beta }_k+{\mu }_1\\ 1\times {\beta }_1+X_{22}{\beta }_2+X_{32}{\beta }_3+...+X_{k2}{\beta }_k+{\mu }_2\\ ...\\ 1\times {\beta }_1+X_{2n}{\beta }_2+X_{3n}{\beta }_3+...+X_{kn}{\beta }_k+{\mu }_n\end{array}\right]\end{array}$$

---

作为简化，用一个行矩阵乘以一个列矩阵，即求该矩阵的第一个数字的过程，即
$$\begin{array}{c}\left[\begin{array}{ccccc}1& X_{21}& X_{31}& ...& X_{k1}\end{array}\right]\left[\begin{array}{c}{\beta }_1\\ {\beta }_2\\ {\beta }_3\\ ...\\ {\beta }_k\end{array}\right]\end{array}=\begin{array}{c}\left[\begin{array}{c}1\times {\beta }_1+X_{21}{\beta }_2+X_{31}{\beta }_3+...+X_{k1}{\beta }_k\end{array}\right]\end{array}$$
如果交换两个矩阵位置再相乘，则会得到下边结果：
$$\begin{array}{c}\left[\begin{array}{c}{\beta }_1\\ {\beta }_2\\ {\beta }_3\\ ...\\ {\beta }_k\end{array}\right]\left[\begin{array}{ccccc}1& X_{21}& X_{31}& ...& X_{k1}\end{array}\right]=\left[\begin{array}{ccccc}{\beta }_1\times 1& {\beta }_2{X}_{21}& {\beta }_3{X}_{31}& ...& {\beta }_k{X}_{k1}\\ {\beta }_1\times 1& {\beta }_2{X}_{22}& {\beta }_3{X}_{32}& ...& {\beta }_k{X}_{k2}\\ ...& ...& ...& ...& ...\\ {\beta }_1\times 1& {\beta }_2{X}_{2n}& {\beta }_3{X}_{3n}& ...& {\beta }_k{X}_{kn}\end{array}\right]\end{array}$$

当矩阵B有多列时。
当矩阵B有多列时，即使用矩阵A对矩阵B的每一列做上述情景的运算，并在对应位置处生成多列即可。

---

4.4 矩阵的幂

有矩阵的乘法，就可以定义矩阵的幂：
当A是n阶方阵时，$A$与自身的乘法可以用幂的形式来表示，如$A^k$。

---

4.5 交换率结合率分配率汇总

$A+B=B+A$
$(A+B)+C=A+(B+C)$
 
$(\lambda \mu )A=\lambda (\mu A)$
$(\lambda +\mu )A=\lambda A+\mu A$
$\lambda (A+B)=\lambda A+\lambda B$
 
$(AB)C=A(BC)$
$\lambda (AB)=(\lambda A)B=A(\lambda B)$
$A(B+C)=AB+AC$   $(B+C)A=BA+CA$

对单位矩阵有：
        $E_m{A}_{m\times n}=A_{m\times n}{E}_n=A$

对矩阵的幂：
            $A^k{A}^l=A^{k+l}$
只有当$AB$中A与B可交换位置时（可交换位置不限于两者相等），才有$(AB{)}^k=A^k{B}^k$。

---

4.6 矩阵的转置

转置即行列互换。
 
矩阵的转置满足以下运算规律：
 
$(A^T{)}^T=A$
$(A+B{)}^T=A^T+B^T$
$(\lambda A{)}^T=\lambda A^T$
$(AB{)}^T=B^T{A}^T$

设A为n阶方阵，如果满足$A^T=A$，即$a_{ij}=a_{ji}$，则A被称为 对称矩阵，简称对矩阵。对称矩阵中以对角线为对称轴的元素相等。

---

5. 矩阵的行列式

矩阵A的行列式记作$|A|$或$detA$。
不是所有的矩阵都可以变为行列式，方阵才可以。
由矩阵确定的行列式在计算时满足：
     $|A^T|=|A|$
     $|\lambda A|={\lambda }^n|A|$
     $|AB|=|A||B|$

行列式$|A|$的各个元素的代数余子式$A_{ij}$构成的如下矩阵，
 
                 $A\ast =\left[\begin{array}{cccc}{A}_{11}& A_{21}& ...& A_{n1}\\ A_{12}& A_{22}& ...& A_{n2}\\ ...& ...& ...& ...\\ A_{1n}& A_{2n}& ...& A_{nn}\end{array}\right]$
矩阵$A\ast$称为矩阵A的 伴随矩阵。简称伴随阵。

矩阵$A$与它的伴随矩阵$A\ast$满足：
 
               $AA\ast =A\ast A=|A|E$

---

6.矩阵的线性变换

对等式：
$$\left[\begin{array}{cccc}{a}_{11}& a_{12}& ...& a_{1n}\\ a_{21}& a_{22}& ...& a_{2n}\\ ...& ...& ...& ...\\ a_{m1}& a_{m2}& ...& a_{mn}\end{array}\right]\times \left[\begin{array}{c}{x}_1\\ x_2\\ ...\\ x_n\end{array}\right]=\left[\begin{array}{c}{y}_1\\ y_2\\ ...\\ y_n\end{array}\right]$$
如果将其看作是一个对$X_{ij}$所在矩阵的变换过程，这样的变换被称作从变量$[x_1,x_2,...,x_n]$到变量$[y_1,y_2,...,y_n]$的 线性变换。其中$a_{ij}$是常数。
 
其中，$a_{ij}$所构成的矩阵被称为 系数矩阵。
矩阵的线性变换在实际应用中是非常重要的。
 
系数矩阵确定，变换关系就确定。
 
下边给出几个典型示例：
①对角矩阵对$[x_1,x_2,...x_n]$的线性变换
$$\left[\begin{array}{cccc}{\lambda }_1& 0& ...& 0\\ 0& {\lambda }_2& ...& 0\\ ...& ...& ...& ...\\ 0& 0& ...& {\lambda }_n\end{array}\right]\times \left[\begin{array}{c}{x}_1\\ x_2\\ ...\\ x_n\end{array}\right]=\left[\begin{array}{c}{\lambda }_1{x}_1\\ {\lambda }_2{x}_2\\ ...\\ {\lambda }_n{x}_n\end{array}\right]$$
 
②单位矩阵对应的线性变换叫做恒等变换。（单位矩阵的矩阵乘法中的作用类似于1）
$$\left[\begin{array}{cccc}1& 0& ...& 0\\ 0& 1& ...& 0\\ ...& ...& ...& ...\\ 0& 0& ...& 1\end{array}\right]\times \left[\begin{array}{c}{x}_1\\ x_2\\ ...\\ x_n\end{array}\right]=\left[\begin{array}{c}{x}_1\\ x_2\\ ...\\ x_n\end{array}\right]$$
③把向量$A=\left[\begin{array}{cc}x& y\end{array}\right]$沿x轴正方向旋转$\phi$度。得到向量$B=\left[\begin{array}{cc}X& Y\end{array}\right]$
$$\left[\begin{array}{cc}cos\phi & -sin\phi \\ sin\phi & cos\phi \end{array}\right]\times \left[\begin{array}{c}x\\ y\end{array}\right]=\left[\begin{array}{c}X\\ Y\end{array}\right]$$
这也是PCA降维算法的核心思想的一部分。
假设A是有两个特征的样本集，以三个样本为例，则表达式如下：
$$\left[\begin{array}{cc}cos\phi & -sin\phi \\ sin\phi & cos\phi \end{array}\right]\times \left[\begin{array}{ccc}{x}_1& x_2& x_3\\ y_1& y_2& y_3\end{array}\right]=\left[\begin{array}{ccc}{X}_1& X_2& X_3\\ Y_1& Y_2& Y_3\end{array}\right]$$

---

6.逆矩阵

对n阶矩阵A，如果存在n阶矩阵B，使$AB=BA=E$，则称矩阵A是可逆的。矩阵B是矩阵A的逆矩阵。简称逆阵。
 
如果矩阵A是可逆的，那么A的逆矩阵是唯一的唯一的。
 
矩阵A的逆矩阵可以记作$A^{-1}$。
 
定理一
若矩阵A可逆，则$|A|\ne 0$。
 
定理二
如果$|A|\ne 0$，则矩阵A可逆，且
             $A^{-1}=\frac{1}{|A|}A\ast$

当|A|=0时，称为奇异矩阵，否则称为非奇异矩阵。也就是说，奇异矩阵是非可逆矩阵，而非奇异矩阵据说可逆矩阵。所以可逆矩阵的充分必要条件是，$|A|\ne 0$。

所以若A可逆，则A满足：
①$(A^{-1}{)}^{-}1=A$
 
②$(\lambda A{)}^{-1}=\frac{1}{\lambda }{A}^{-1}$
 
③$(AB{)}^{-1}=B^{-1}{A}^{-1}$

---

7.克拉默法则

对有n个未知数和n个线性方程的线性方程组：

      $a_{11}{x}_1+a_{12}{x}_2+...+a_{1n}{x}_n=b_1$
      $a_{21}{x}_1+a_{22}{x}_2+...+a_{2n}{x}_n=b_2$
      $...$
      $a_{n1}{x}_1+a_{n2}{x}_2+...+a_{nn}{x}_n=b_n$

克拉默法则：
 
如果其系数矩阵A的行列式的值不为0，即
$$|A|=\left|\begin{array}{cccc}{a}_{11}& a_{12}& ...& a_{1n}\\ a_{21}& a_{22}& ...& a_{2n}\\ ...& ...& ...& ...\\ a_{n1}& a_{n2}& ...& a_{nn}\end{array}\right|\ne 0$$

则方程组有唯一解：
 
           $x_j=\frac{|A_j|}{|A|}$

其中A_j是系数矩阵A中第j列用方程组右端的常数项代替后得到的n阶矩阵。

---

8.矩阵分块

对于行数和列数较多的矩阵，可以使用分块法将大矩阵分割为小矩阵。每一个小矩阵称为A的 子块，以子块为元素的矩阵称为分块矩阵。分块的方式自由多样。具体不再过多赘述。

---

9.python实现

9.1 创建一般矩阵

可以使用numpy库的mat()方法创建简单矩阵。
创建矩阵时，参数可以采用字符串形式传入，数据之间用空格隔开，行之间用引号隔开。
也可以将numpy数组转化为矩阵。

import numpy as np
# 1.创建一个2×2的矩阵
a1 = np.mat("1 2;3 4")
print(a1)
print("==========================")
# 2.创建一个3×3的矩阵
a2 = np.mat("1 2 3;4 5 6;7 8 9")
print(a2)
print("==========================")
# 3.使用numpy数组创建矩阵
a3 = np.mat(np.random.randint(1, 100, size=(5, 5)))
print(a3)
print("==========================")
print(type(a1))
print(type(a2))
print(type(a3))

输出结果如下：
          

---

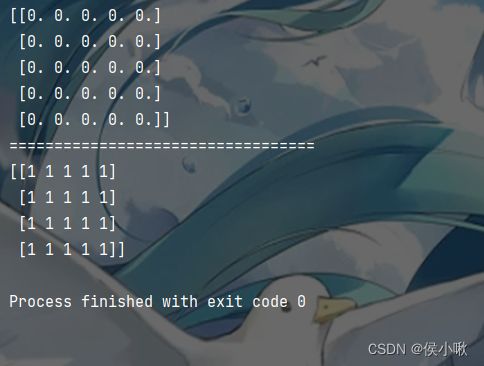
9.2 创建全零、全一矩阵

创建全零矩阵和全一矩阵的代码如下：

# 全零矩阵
m = np.mat(np.zeros((5, 5)))
print(m)
# 全一矩阵
n = np.mat(np.ones((4, 5), dtype='i8'))
print(n)

程序输出结果如下：
          

---

9.3 创建对角矩阵与单位矩阵

创建对角矩阵和单位矩阵的代码如下：

# 对角矩阵
a = [1, 2, 3, 4, 5]
m = np.mat(np.diag(a))
print(m)
print("==================================")
# 单位矩阵
n = np.mat(np.eye(5, dtype='i8'))
print(n)

程序输出结果如下：
          

---

9.4 矩阵与标量的运算

m1 = np.mat([[3, 4], [6, 12], [9, 20]])
print(m1)
print("=======================")
print(m1 + 2)
print("=======================")
print(m1 - 2)
print("=======================")
print(m1 * 2)
print("=======================")
print(m1 / 2)

程序计算结果如下：
          

---

9.5 矩阵与矩阵的运算

同型矩阵才能相加，第一个矩阵的列数等于第二个矩阵的行数才能相乘，这一点一定要遵守。如果不是同型矩阵而相加，也有可能不会报错，比如m1+[[3,4]]此处要格外留意。

m1 = np.mat([[3, 4], [6, 12], [9, 20]])
m2 = np.mat([[3, 4], [6, 12]])
print("==========m1===========：")
print(m1)
print("==========m2===========：")
print(m2)
print("======= m1 + m1 =======：")
print(m1 + m1)
print("======= m1 * m2 =======：")
print(m1 * m2)

程序计算结果如下：
          

---

9.6 矩阵的转置

# 矩阵转置
m = np.mat([[3, 4], [6, 12], [9, 20]])
print(m)
print("====================")
print(m.T)

程序计算结果如下：
             

---

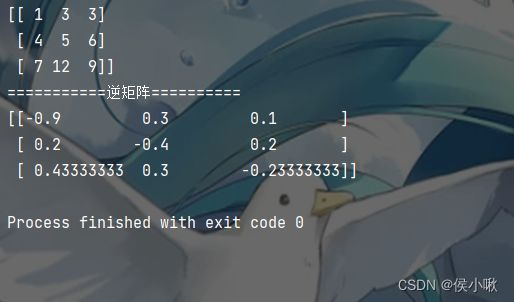
9.7 逆矩阵

m = np.mat("1 3 3;4 5 6;7 12 9")
print(m)
print("===========逆矩阵==========")
print(m.I)

程序计算结果如下：
             

---

本次分享就到这里，小啾感谢您的关注与支持！
꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ꧔ꦿ