常见路径规划算法介绍
本文介绍了算法书上常见的路径规划算法和工业界目前比较流行的高效分层路径规划算法。
目录
目录
1. 经典路径规划算法
1.1 Dijkstra
1.2 Bellman-Ford
1.3 SPFA
1.4 A*
1.5 Bidirectional Search(双向搜索)
2. 分层规划算法
2.1 CH算法 (Contraction Hierarchies)
2.1.1 CH预处理
2.1.2 CH查询
2.2 CCH算法 (Customizable Contraction Hierarchies)
2.3 CRP算法(Customizable Route Planning)
2.3.1 Overlay Graph(覆盖图)
2.3.2 覆盖图剪枝
2.3.3 预处理阶段
2.3.4 定制化阶段
2.3.5 查询阶段
3.参考文献:
1. 经典路径规划算法
1.1 Dijkstra
堆优化的实现版本,时间复杂度为O(E+VlogV)
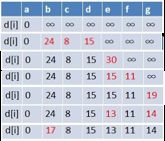
1.2 Bellman-Ford
算法伪代码如下:
bool Bellman-Ford(G,w,s) //图G
for each vertex v ∈ V(G): //初始化
d[v] ←+∞
d[s] ←0 //源点距离自身为0
for i = 1 → |V|:
for each edge (u,v) ∈ E(G):
if d[v] > d[u] + w(u,v):
d[v] = d[u] + w(u,v)
for each edge(u,v) ∈ E(G): //判断负权环路
if d[v] > d[u] + w(u,v):
return false
return true1.3 SPFA
算法伪代码如下:
ProcedureSPFA;
Begin
initialize-single-source(G,s);
initialize-queue(Q);
enqueue(Q,s);
while not empty(Q) do begin
u:=dequeue(Q);
for each v∈adj[u] do begin
tmp:=d[v];
relax(u,v);
if(tmp<>d[v])and(not v in Q)then enqueue(Q,v);
end;
end;
End;
1.4 A*
A*算法的估算函数为:f(n)=g(n)+h(n)
启发函数可以是欧式距离、曼哈顿距离等
1.5 Bidirectional Search(双向搜索)
2. 分层规划算法
主要分两种策略,第一种是针对交通网的,利用交通网本身所具有的分层特性,利用干道和支路对网络进行分层。这种策略应用面相对较窄,而且对网络的识别和预处理复杂,甚至需要人工干预。第二种策略即人工对网络进行分割构造分层结构,通过人工分割使各子网规模大致均等,并尽量使得分割后的子网相互独立。
2.1 CH算法 (Contraction Hierarchies)
2.1.1 CH预处理
1.生成node order
节点收缩顺序决定了预处理的性能
两种节点顺序试探法:1.自下而上 2.自上而下
自下而上采用贪心算法收缩完一个节点再处理一个节点
自上而下式在第一个节点收缩前预先计算整个节点顺序。效果更好,需要更多处理时间。嵌套解剖分割图。
增加虚拟的shortcut,以减少需要搜索的节点
2.1.2 CH查询
1.Query
2. Path Unpack
将shortcut解压为原始路径
2.2 CCH算法 (Customizable Contraction Hierarchies)
使用Inertial Flow算法计算node order,可离线运行,保存到文件供在线定制查询使用。
权值变化时使用变化后的权值更新权值相关的metric(定制化),支持并行更新和增量更新
和CH算法相同,双向搜索然后unpack path。
CCH特点:
预处理数分钟到数小时,定制化秒级,查询毫秒级
可以很好地适应权值变化,支持多套权值,易于扩展
2.3 CRP算法(Customizable Route Planning)
分为三个阶段:
3.Query: 查询阶段
2.3.1 Overlay Graph(覆盖图)
覆盖图的特点:
level-l中的所有boundary arc以及所有shortcut是level-(l-1)的覆盖图
2.3.2 覆盖图剪枝
保存cell中每一个clique有些浪费,很多不在最短路径上,可以对其剪枝
reduction: 针对每两个boundary vertex在本层graph上进行Dijkstra搜索,把不是shortcut 的边删除。
skeleton graph:针对每个boundary vertex计算到当前cell内其他boundary vertex的最短路径树,最后对所有的最短路径树求并集构造为 skeleton graph。
2.3.3 预处理阶段
使用PUNCH算法将图分割为多层overlay graph,存储为辅助数据,供定制化和查询使用
图分割的目标是overlay graph中boundary arc的数目尽量少,这会使定制化阶段耗费的时间和空间更少,路径查询更快
PUNCH算法的原理是利用路网中自然分割(河流,山川,高速公路)作为启发因子进行分割。
预处理结果为一个多层的overlay graph, 每一个node都存在于各个level的cell中,每个level中boundary vertex不同。一个cell有p个入口节点,q个出口节点,就会有p*q个shortcut。
2.3.4 定制化阶段
采用自底向上的方式更新各个level中每个cell的shortcut权值
定制化与查询同时进行,因此定制化需要足够快
加速定制化的方法:
2.3.5 查询阶段
找出node v与起终点没有交集的最大level(query level),迭代搜索。
crp 为了节省内存,没有存储shortcut 对应的原始路径,需要双向搜索计算出shortcut中的原始路径
3.参考文献:
Contraction Hierarchies: Faster and Simpler Hierarchical Routing in Road Networks
Customizable Route Planning in Road Networks
Customizable Route Planning
Customizable Contraction Hierarchies
Graph Partitioning with Natural Cuts