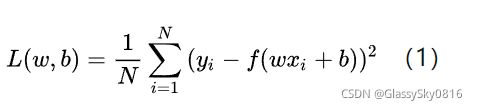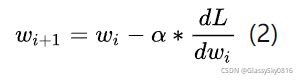梯度下降算法(Gradient Descent)的原理和实现步骤
梯度下降的目的
绝大多数的机器学习模型都会有一个损失函数。比如常见的均方误差(Mean Squared Error)损失函数:
损失函数用来衡量机器学习模型的精确度。一般来说,损失函数的值越小,模型的精确度就越高。如果要提高机器学习模型的精确度,就需要尽可能降低损失函数的值。而降低损失函数的值,我们一般采用梯度下降这个方法。所以,梯度下降的目的,就是为了最小化损失函数。
梯度下降的原理
寻找损失函数的最低点,就像我们在山谷里行走,希望找到山谷里最低的地方。那么如何寻找损失函数的最低点呢?在这里,我们使用了微积分里导数,通过求出函数导数的值,从而找到函数下降的方向或者是最低点(极值点)。
损失函数里一般有两种参数,一种是控制输入信号量的权重(Weight, 简称 ![]() ),另一种是调整函数与真实值距离的偏差(Bias,简称 b )。我们所要做的工作,就是通过梯度下降方法,不断地调整权重 和偏差b,使得损失函数的值变得越来越小。
),另一种是调整函数与真实值距离的偏差(Bias,简称 b )。我们所要做的工作,就是通过梯度下降方法,不断地调整权重 和偏差b,使得损失函数的值变得越来越小。
假设某个损失函数里,模型损失值 与权重 w 有下图这样的关系。实际模型里,可能会有多个权重 ,这里为了简单起见,举只有一个权重 的例子。权重 目前的位置是在A点。此时如果求出A点的梯度 ,便可以知道如果我们向右移动,可以使损失函数的值变得更小。
通过计算梯度,我们就可以知道 ![]() 的移动方向,应该让 w 向右走而不是向左走,也可以知道什么时候会到达最低点(梯度为0的地方)。
的移动方向,应该让 w 向右走而不是向左走,也可以知道什么时候会到达最低点(梯度为0的地方)。
上面的例子里只出现了一个权重![]() , 实际的项目里样本数据会有很多个。对于每一个样本数据,我们都可以求出一个权重的梯度。这个时候,我们需要把各个样本数据的权重梯度加起来,并求出它们的平均值,用这个平均值来作为样本整体的权重梯度。
, 实际的项目里样本数据会有很多个。对于每一个样本数据,我们都可以求出一个权重的梯度。这个时候,我们需要把各个样本数据的权重梯度加起来,并求出它们的平均值,用这个平均值来作为样本整体的权重梯度。
现在知道了 ![]() 需要前进的方向,接下来需要知道应该前进多少。这里我们用到学习率(Learning Rate)这个概念。通过学习率,可以计算前进的距离(步长)。
需要前进的方向,接下来需要知道应该前进多少。这里我们用到学习率(Learning Rate)这个概念。通过学习率,可以计算前进的距离(步长)。
我们用 ![]() 表示权重的初始值, w_i+1 表示更新后的权重值,用 表示学习率,则有:
表示权重的初始值, w_i+1 表示更新后的权重值,用 表示学习率,则有:
在梯度下降中,我们会重复式子(2)多次,直至损失函数值收敛不变。
如果学习率 ![]() 设置得过大,有可能我们会错过损失函数的最小值;如果设置得过小,可能我们要迭代式子(2)非常多次才能找到最小值,会耗费较多的时间。因此,在实际应用中,我们需要为学习率
设置得过大,有可能我们会错过损失函数的最小值;如果设置得过小,可能我们要迭代式子(2)非常多次才能找到最小值,会耗费较多的时间。因此,在实际应用中,我们需要为学习率 ![]() 设置一个合适的值。
设置一个合适的值。
上面讲解了对权重 ![]() 值的优化过程,对于偏差 b ,我们也可以用相同的方式进行处理,这里就不再展开了。
值的优化过程,对于偏差 b ,我们也可以用相同的方式进行处理,这里就不再展开了。
梯度下降的过程
for i = 0 to 训练数据的个数:
- 计算第 i 个训练数据的权重
 和偏差 b 相对于损失函数的梯度。于是我们最终会得到每一个训练数据的权重和偏差的梯度值。
和偏差 b 相对于损失函数的梯度。于是我们最终会得到每一个训练数据的权重和偏差的梯度值。 - 计算所有训练数据权重
 的梯度的总和。
的梯度的总和。 - 计算所有训练数据偏差
 的梯度的总和。
的梯度的总和。
做完上面的计算之后,我们开始执行下面的计算:
- 使用上面第(2)、(3)步所得到的结果,计算所有样本的权重和偏差的梯度的平均值。
- 使用下面的式子,更新每个样本的权重值和偏差值。
重复上面的过程,直至损失函数收敛不变。
def train(X, y, W, B, alpha, max_iters):
'‘’
选取所有的数据作为训练样本来执行梯度下降
X : 训练数据集
y : 训练数据集所对应的目标值
W : 权重向量
B : 偏差变量
alpha : 学习速率
max_iters : 梯度下降过程最大的迭代次数
'''
dW = 0 # 初始化权重向量的梯度累加器
dB = 0 # 初始化偏差向量的梯度累加器
m = X.shape[0] # 训练数据的数量
# 开始梯度下降的迭代
for i in range(max_iters):
dW = 0 # 重新设置权重向量的梯度累加器
dB = 0 # 重新设置偏差向量的梯度累加器
# 对所有的训练数据进行遍历
for j in range(m):
# 1. 遍历所有的训练数据
# 2. 计算每个训练数据的权重向量梯度w_grad和偏差向量梯度b_grad
# 3. 把w_grad和b_grad的值分别累加到dW和dB两个累加器里
W = W - alpha * (dW / m) # 更新权重的值
B = B - alpha * (dB / m) # 更新偏差的值
return W, B # 返回更新后的权重和偏差。总结
梯度下降法实现简单,当目标函数是凸函数时,梯度下降法的解是全局解。
缺点:
靠近极小值时收敛速度减慢,求解需要很多次的迭代;
一般情况下,其解不保证是全局最优解,梯度下降法的速度也未必是最快的。