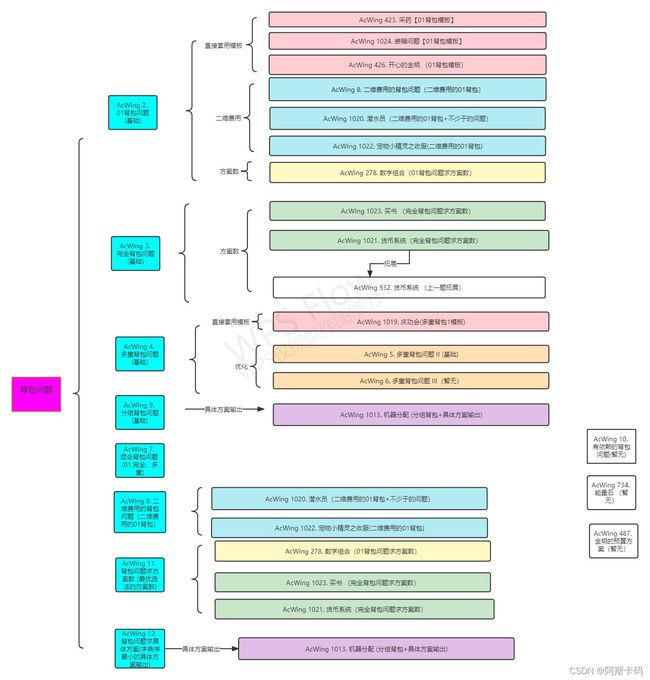
背包问题(基本全)

喔是宝藏UP

AcWing 2. 01背包问题(基础)

有 N 件物品和一个容量是 V的背包。每件物品只能使用一次。

第 i件物品的体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。
输入格式
第一行两个整数，N，V，用空格隔开，分别表示物品数量和背包容积。

接下来有 N行，每行两个整数 vi,wi，用空格隔开，分别表示第 i件物品的体积和价值。
输出格式
输出一个整数，表示最大价值。
数据范围

0

输入样例

4 5
1 2
2 4
3 4
4 5

输出样例：

8

二维01[AC]

#include
using namespace std;
const int N=1010;
int w[N],v[N],f[N][N];
int n,m;
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)cin>>v[i]>>w[i];
    
    
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            f[i][j]=f[i-1][j];
            if(j>=v[i])f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]);
        }
    }
    cout<<f[n][m]<<endl;
}

优化思路:二维–>一维

一维01[AC]

#include
using namespace std;

const int N=1010;
int n,m;
int v[N],w[N],f[N];
//f[i]:N 件物品，背包容量j下的最优解。
//删除第一维
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)cin>>v[i]>>w[i];
    
    for(int i=1;i<=n;i++)
    {
        //m-->v[i]先计算大的，即f[i][j-v[i]]
        //v[i]-->m先计算小的，即f[i-1][j-v[i]]
        for(int j=m;j>=v[i];j--)
        {
            //f[i][j]=f[i-1][j];
            //f[j]=f[j]
            
            //if(j>=v[i])f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]);
            //f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]);
            
            //v[i]-->m
            //如果删除第一维：f[j]=max(f[j],f[j-v[i]]+w[i])
            //等价于f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);
            
            //m-->v[i]
            //如果删除第一维：f[j]=max(f[j],f[j-v[i]]+w[i])
            //等价于f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]);
            
            //原因：
            //eg:v[i]-->m先计算小的，i=1时，由于j-v[1]
            //在计算f[j]=max(f[j],f[j-v[i]]+w[i])时,用到的是f[1][j-v[1]]+w[i]
            //eg:m-->v[i]先计算大的，i=1时，由于j-v[1]
            //在计算f[j]=max(f[j],f[j-v[i]]+w[i])时,用到的是f[0][j-v[i]]+w[i]
            
            f[j]=max(f[j],f[j-v[i]]+w[i]);
        }   
        
    }
    
    cout<<f[m]<<endl;
}

AcWing 3. 完全背包问题(基础)

有 N 种物品和一个容量是 V的背包，每种物品都有无限件可用。

第 i种物品的体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。输出最大价值。
输入格式
第一行两个整数，N，V，用空格隔开，分别表示物品种数和背包容积。

接下来有 N行，每行两个整数 vi,wi，用空格隔开，分别表示第 i种物品的体积和价值。
输出格式

输出一个整数，表示最大价值。
数据范围

0

0

输入样例

4 5
1 2
2 4
3 4
4 5

输出样例：

10

//01:f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]);
//完全：f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);

//01：f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]);-->用到的是f[i-1][....]故从大到小循环即可
//完全：f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);-->用到的是f[i][....]故从小到大循环即可

//为什么可以2个for:
//因为            
// for(int j=1;j<=m;j++)
// {
//     for(int k=0;k*v[i]<=j;k++)
//     {
//         f[i][j]=max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);
//     }
// }
//可以转换

三维[TLE]

#include
using namespace std;
const int N=1010;
int w[N],v[N],f[N][N];
int n,m;

int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)cin>>v[i]>>w[i];
    
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            for(int k=0;k*v[i]<=j;k++)
            {
                f[i][j]=max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);
            }
            
        }
    }
    
    cout<<f[n][m]<<endl;
}

优化思路:三for–>二for

二维/一维[AC]【优化：与01背包相同】

#include
using namespace std;
const int N=1010;
int w[N],v[N],f[N][N];
int n,m;

int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)cin>>v[i]>>w[i];
    
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            f[i][j]=f[i-1][j];
            if(j>=v[i])f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);
        }
    }
    
    cout<<f[n][m]<<endl;
}

#include
using namespace std;
const int N=1010;
int w[N],v[N],f[N];
int n,m;

int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)cin>>v[i]>>w[i];
    
    for(int i=1;i<=n;i++)
    {
        for(int j=v[i];j<=m;j++)
        {
            f[j]=max(f[j],f[j-v[i]]+w[i]);
            //f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);-->用到的是f[i][....]故从小到大循环即可
            //f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]);-->用到的是f[i-1][....]故从大到小循环即可
        }
    }
    cout<<f[m]<<endl;
}

AcWing 4. 多重背包问题(基础)

有 N 种物品和一个容量是 V的背包。

第 i种物品最多有 si 件，每件体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。输出最大价值。
输入格式

第一行两个整数，N，V，用空格隔开，分别表示物品种数和背包容积。

接下来有 N行，每行三个整数 vi,wi,si，用空格隔开，分别表示第 i种物品的体积、价值和数量。
输出格式

输出一个整数，表示最大价值。
数据范围

0

0

输入样例

4 5
1 2 3
2 4 1
3 4 3
4 5 2

输出样例：

10

//为什么必须三个for:
//因为            //
//for(int k=0;k<=s[i];k++)
//{
//    if(j>=k*v[i])
//    f[i][j]=max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);
//}
//无法转换

三维[AC]–不能像完全背包的二维优化【原因】

#include
using namespace std;

const int N=110;
int n,m;
int v[N],w[N],s[N];
int f[N][N];
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)cin>>v[i]>>w[i]>>s[i];
    
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            for(int k=0;k<=s[i];k++)
            {
                if(j>=k*v[i])
                f[i][j]=max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);
            }
        }
    }
    
    cout<<f[n][m]<<endl;
}

AcWing 5. 多重背包问题 II (基础)

有 N 种物品和一个容量是 V的背包。

第 i种物品最多有 si 件，每件体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。输出最大价值。
输入格式

第一行两个整数，N，V，用空格隔开，分别表示物品种数和背包容积。

接下来有 N行，每行三个整数 vi,wi,si，用空格隔开，分别表示第 i种物品的体积、价值和数量。
输出格式

输出一个整数，表示最大价值。
数据范围

0

0 0

提示：

本题考查多重背包的二进制优化方法。
输入样例

4 5
1 2 3
2 4 1
3 4 3
4 5 2

输出样例：

10

优化思路:三维–>01背包问题【二维/一维】

二维[AC]–数据范围变大–二进制优化

//做法：将10分成1,2,4,3
//        16    1,2,4,8,1
//将1，2，4，3，1，2，4，8，1分别变成一个新的物品，然后进行01背包
//原因：复杂度小，而且可以进行组合，变成需要的数量

#include
using namespace std;
const int N=1000*15;//1000*log 2000
int a,b,c,cnt;
int n,m;
int f[N];
int v[N],w[N],s[N];
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        cin>>a>>b>>c;
        int k=1;//代表捆绑之后的物品个数；
        while(c>=k)
        {
            cnt++;//cnt=[1,n]
            v[cnt]=k*a;
            w[cnt]=k*b;
            c=c-k;
            k=2*k;
        }
        if(c>0)
        {
            
            cnt++;//cnt=1
            v[cnt]=c*a;
            w[cnt]=c*b;
        }
    }
    
    
    int n1=cnt;//捆绑之后的商品数量
    for(int i=1;i<=n1;i++)
    {
        for(int j=m;j>=v[i];j--)
        {
            f[j]=max(f[j],f[j-v[i]]+w[i]);
        }
    }
    
    cout<<f[m]<<endl;
}

AcWing 9. 分组背包问题(基础)

有 N 组物品和一个容量是 V的背包。

每组物品有若干个，同一组内的物品最多只能选一个。
每件物品的体积是 vij，价值是 wij，其中 i 是组号，j是组内编号。

求解将哪些物品装入背包，可使物品总体积不超过背包容量，且总价值最大。

输出最大价值。
输入格式

第一行有两个整数 N，V，用空格隔开，分别表示物品组数和背包容量。

接下来有 N组数据：
每组数据第一行有一个整数 Si，表示第 i个物品组的物品数量；每组数据接下来有 Si行，每行有两个整数 vij,wij，用空格隔开，分别表示第 i 个物品组的第 j 个物品的体积和价值；

输出格式
输出一个整数，表示最大价值。

数据范围
0 0 0

输入样例

3 5
2
1 2
2 4
1
3 4
1
4 5

输出样例：

8

二维/一维[AC]【优化：与01背包相同】

//为什么必须三个for:
//因为必须要用到k
#include
using namespace std;
const int N=110;
int n,m;
int s[N],v[N][N],w[N][N],f[N][N],dp[N];
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        cin>>s[i];
        for(int j=1;j<=s[i];j++)
        cin>>v[i][j]>>w[i][j];
    }

    //二维
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            f[i][j]=f[i-1][j];//0
            for(int k=1;k<=s[i];k++)
            if(j>=v[i][k])
               f[i][j]=max(f[i][j],f[i-1][j-v[i][k]]+w[i][k]);//1.....s[i]
        }
    }
    cout<<f[n][m]<<endl;
    return 0;
}

//为什么必须三个for:
//因为必须要用到k
#include
using namespace std;
const int N=110;
int n,m;
int s[N],v[N][N],w[N][N],f[N][N],dp[N];
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        cin>>s[i];
        for(int j=1;j<=s[i];j++)
        cin>>v[i][j]>>w[i][j];
    }
    //一维
    for(int i=1;i<=n;i++)
        for(int j=m;j>=0;j--)
            for(int k=0;k<=s[i];k++)
            if(j>=v[i][k])dp[j]=max(dp[j],dp[j-v[i][k]]+w[i][k]);
    
    cout<<dp[m]<<endl;
    return 0;
}

AcWing 423. 采药(01背包模板)

辰辰是个天资聪颖的孩子，他的梦想是成为世界上最伟大的医师。

为此，他想拜附近最有威望的医师为师。

医师为了判断他的资质，给他出了一个难题。

医师把他带到一个到处都是草药的山洞里对他说：“孩子，这个山洞里有一些不同的草药，采每一株都需要一些时间，每一株也有它自身的价值。我会给你一段时间，在这段时间里，你可以采到一些草药。如果你是一个聪明的孩子，你应该可以让采到的草药的总价值最大。”

如果你是辰辰，你能完成这个任务吗？
输入格式

输入文件的第一行有两个整数 T和 M，用一个空格隔开，T 代表总共能够用来采药的时间，M

代表山洞里的草药的数目。

接下来的 M行每行包括两个在 1 到 100 之间（包括 1 和 100
）的整数，分别表示采摘某株草药的时间和这株草药的值。
输出格式
输出文件包括一行，这一行只包含一个整数，表示在规定的时间内，可以采到的草药的最大总价值。
数据范围

1≤T≤1000,
1≤M≤100

输入样例：

70 3
71 100
69 1
1 2

输出样例：

3

二维/一维[AC]【优化：与01背包相同】

//二维
#include
using namespace std;

const int N=1010;
int n,m;
int v[N],w[N],f[N][N];
int main()
{
    cin>>m>>n;//m=V n=商品个数
 
    for(int i=1;i<=n;i++)cin>>v[i]>>w[i];
    
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            f[i][j]=f[i-1][j];
            if(j>=v[i])f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]);
        }
    }
    cout<<f[n][m]<<endl;
}

//一维
#include
using namespace std;
const int N=1010;
int v[N],w[N],f[N];
int n,m;
int main()
{
    cin>>m>>n;
    for(int i=1;i<=n;i++)cin>>v[i]>>w[i];
    
    for(int i=1;i<=n;i++)//商品数量
        for(int j=m;j>=v[i];j--)//体积
            f[j]=max(f[j],f[j-v[i]]+w[i]);
            
    cout<<f[m]<<endl;
}

AcWing 1024. 装箱问题(01背包模板)

有一个箱子容量为 V，同时有 n 个物品，每个物品有一个体积（正整数）。

要求 n 个物品中，任取若干个装入箱内，使箱子的剩余空间为最小。
输入格式

第一行是一个整数 V，表示箱子容量。
第二行是一个整数 n，表示物品数。

接下来 n 行，每行一个正整数（不超过10000），分别表示这 n 个物品的各自体积。
输出格式

一个整数，表示箱子剩余空间。
数据范围

0 0

输入样例：

24
6
8
3
12
7
9
7

输出样例：

0

二维/一维[AC]【优化：与01背包相同】

//二维
//01背包
#include
using namespace std;
const int N=20000+10;
int v[N],f[N][N];
int n,m;
int main()
{
    cin>>m;//容量
    cin>>n;//商品个数
    for(int i=1;i<=n;i++)cin>>v[i];
    
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            f[i][j]=f[i-1][j];//0
            if(j>=v[i])f[i][j]=max(f[i][j],f[i-1][j-v[i]]+v[i]);//1
        }
    }
    cout<<m-f[n][m]<<endl;
}

//一维
//01背包
#include
using namespace std;
const int N=20000+10;
int v[N],f[N],w[N];
int n,m;
int main()
{
    cin>>m;//容量
    cin>>n;//商品个数
    for(int i=1;i<=n;i++)
    {
        cin>>v[i];
        w[i]=v[i];
    }
    for(int i=1;i<=n;i++)
        for(int j=m;j>=v[i];j--)
            f[j]=max(f[j],f[j-v[i]]+w[i]);
            
    cout<<m-f[m]<<endl;
}

AcWing 1022. 宠物小精灵之收服(二维费用的01背包)

宠物小精灵是一部讲述小智和他的搭档皮卡丘一起冒险的故事。

一天，小智和皮卡丘来到了小精灵狩猎场，里面有很多珍贵的野生宠物小精灵。

小智也想收服其中的一些小精灵。

然而，野生的小精灵并不那么容易被收服。

对于每一个野生小精灵而言，小智可能需要使用很多个精灵球才能收服它，而在收服过程中，野生小精灵也会对皮卡丘造成一定的伤害（从而减少皮卡丘的体力）。

当皮卡丘的体力小于等于0时，小智就必须结束狩猎（因为他需要给皮卡丘疗伤），而使得皮卡丘体力小于等于0的野生小精灵也不会被小智收服。

当小智的精灵球用完时，狩猎也宣告结束。

我们假设小智遇到野生小精灵时有两个选择：收服它，或者离开它。

如果小智选择了收服，那么一定会扔出能够收服该小精灵的精灵球，而皮卡丘也一定会受到相应的伤害；如果选择离开它，那么小智不会损失精灵球，皮卡丘也不会损失体力。

小智的目标有两个：主要目标是收服尽可能多的野生小精灵；如果可以收服的小精灵数量一样，小智希望皮卡丘受到的伤害越小（剩余体力越大），因为他们还要继续冒险。

现在已知小智的精灵球数量和皮卡丘的初始体力，已知每一个小精灵需要的用于收服的精灵球数目和它在被收服过程中会对皮卡丘造成的伤害数目。

请问，小智该如何选择收服哪些小精灵以达到他的目标呢？
输入格式

输入数据的第一行包含三个整数：N，M，K，分别代表小智的精灵球数量、皮卡丘初始的体力值、野生小精灵的数量。

之后的K行，每一行代表一个野生小精灵，包括两个整数：收服该小精灵需要的精灵球的数量，以及收服过程中对皮卡丘造成的伤害。
输出格式

输出为一行，包含两个整数：C，R，分别表示最多收服C个小精灵，以及收服C个小精灵时皮卡丘的剩余体力值最多为R。
数据范围

0 0 0

输入样例1：

10 100 5
7 10
2 40
2 50
1 20
4 20

输出样例1：

3 30

输入样例2：

10 100 5
8 110
12 10
20 10
5 200
1 110

输出样例2：

0 100

二维[AC]

//三维/二维

//宠物小精灵之收服 ：max
//f[i][j][k]:前i个物品，花费1<=j,花费2<=k 的方案的最大值(k代表皮卡丘的使用的体力)
//由于皮卡丘体力小于等于0的野生小精灵也不会被收服
//f[t][n][m-1]:前t个物品，花费1<=n,花费2<=m-1 的方案的最大值(m-1代表皮卡丘的使用的体力)
//所以max=f[i][j][k-1]
//虽然有m体力，但是只有m-1体力对于皮卡丘有意义
#include
using namespace std;
const int N=1010,M=510,K=110;
int f[N][M],ne[K],pika[K];
int n,m,t;
int main()
{
    cin>>n>>m>>t;
    
    for(int i=1;i<=t;i++)cin>>ne[i]>>pika[i];
    
    for(int i=1;i<=t;i++)//物品数量
    {
        for(int j=n;j>=ne[i];j--)//花费1
        {
            for(int k=m;k>=pika[i];k--)//花费2
            {
                f[j][k]=max(f[j][k],f[j-ne[i]][k-pika[i]]+1);
            }
        }
    }
    
    cout<<f[n][m-1]<<" ";
    
    //消耗的体力从0开始
    int k=0;
    while(k<=m&&f[n][k]!=f[n][m-1])k++;
    cout << m - k << endl;
    
}

AcWing 278. 数字组合（01背包问题求方案数）

给定 N 个正整数 A1,A2,…,AN，从中选出若干个数，使它们的和为 M，求有多少种选择方案。
输入格式

第一行包含两个整数 N和 M。

第二行包含 N
个整数，表示 A1,A2,…,AN。
输出格式

包含一个整数，表示可选方案数。
数据范围

1≤N≤100,
1≤M≤10000,
1≤Ai≤1000,
答案保证在 int 范围内。
输入样例：

4 4
1 1 2 2

输出样例：

3

二维/一维[AC]【优化：与01背包相同】

#include
using namespace std;

const int N=110,M=10000+10;
int w[N],f[N][M];
int n,m;

int main()
{
    cin>>n>>m;
    f[0][0]=1;
    for(int i=1;i<=n;i++)//商品个数
    {
        int x;
        cin>>x;
        for(int j=0;j<=m;j++)//总和
        {
            f[i][j]=f[i-1][j];
            if(j>=x)f[i][j]=f[i][j]+f[i-1][j-x];
        }
    }
    cout<<f[n][m]<<endl;
}

//f[i][j]=f[i-1][j]+f[i-1][j-v]
//二维/一维
//初始化
//f[0]=1   f[0][0]=1

#include
using namespace std;

const int N=110,M=10000+10;
int w[N],f[M];
int n,m;

int main()
{
    cin>>n>>m;
    f[0]=1;
    for(int i=1;i<=n;i++)//商品个数
    {
        int x;
        cin>>x;
        for(int j=m;j>=x;j--)//总和
            f[j]=f[j]+f[j-x];
    }
    
    cout<<f[m]<<endl;
}

AcWing 1023. 买书 （完全背包问题求方案数）–类似上一题

小明手里有n元钱全部用来买书，书的价格为10元，20元，50元，100元。

问小明有多少种买书方案？（每种书可购买多本）
输入格式

一个整数 n，代表总共钱数。
输出格式

一个整数，代表选择方案种数。
数据范围

0≤n≤1000

输入样例1：

20

输出样例1：

2

输入样例2：

15

输出样例2：

0

输入样例3：

0

输出样例3：

1

二维/一维[AC]【优化：与01背包相同】

#include
using namespace std;

const int N=1010;

int f[N][N];
int v[5]={0,10,20,50,100};
int n;

int main()
{
    cin>>n;
    f[0][0]=1;
    for(int i=1;i<=4;i++)//物品个数
    {
        for(int j=0;j<=n;j++)//容量总数
        {
            f[i][j]=f[i][j]+f[i-1][j];
            if(j>=v[i])f[i][j]=f[i][j]+f[i][j-v[i]];
        }
    }
    
    cout<<f[4][n]<<endl;
    
    return 0;
}

//完全背包
//给定maxv,求达到最大值的所有方案
#include
using namespace std;

const int N=1010;

int f[N];
int v[5]={0,10,20,50,100};
int n;

int main()
{
    cin>>n;
    f[0]=1;
    for(int i=1;i<=4;i++)//物品个数
    {
        for(int j=v[i];j<=n;j++)//容量总数
        {
            f[j]=f[j]+f[j-v[i]];
        }
    }
    
    cout<<f[n]<<endl;
    
    return 0;
}

AcWing 1021. 货币系统（完全背包问题求方案数）

给你一个n种面值的货币系统，求组成面值为m的货币有多少种方案。
输入格式

第一行，包含两个整数n和m。

接下来n行，每行包含一个整数，表示一种货币的面值。
输出格式

共一行，包含一个整数，表示方案数。
数据范围

n≤15,m≤3000

输入样例：

3 10
1
2
5

输出样例：

10

二维[AC]【优化：与完全背包1相同】

三for

//3for
#include
using namespace std;
int n,m;
long long v[3005],f[3005][3005];
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)cin>>v[i];
    
    f[0][0]=1;
    
    for(int i=1;i<=n;i++)
    {
        for(int j=0;j<=m;j++)
        {
            f[i][j]=f[i-1][j];
            for(int k=1;j>=k*v[i];k++)
            if(j>=k*v[i])f[i][j]=f[i][j]+f[i-1][j-k*v[i]];
        }
    }
    
    cout<<f[n][m]<<endl;
    
}

二for

// f[i][j]     = f[i-1][j]     f[i-1][j-v]   f[i-1][j-2v]   f[i-1][j-3v]  f[i-1][j-4v]  f[i-1][j-sv]
// f[i][j-v]   =               f[i-1][j-v]   f[i-1][j-2v]   f[i-1][j-3v]  f[i-1][j-4v]  f[i-1][j-sv]
// -->
// f[i][j]     = f[i-1][j]  +  f[i][j-v]     

//2for
#include
using namespace std;
int n,m;
long long v[3005],f[3005][3005];
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)cin>>v[i];
    
    f[0][0]=1;
    
    for(int i=1;i<=n;i++)
    {
        for(int j=0;j<=m;j++)
        {
            f[i][j]=f[i-1][j];
            if(j>=v[i])f[i][j]=f[i][j]+f[i][j-v[i]];
        }
    }
    
    cout<<f[n][m]<<endl;
    
}

一维[AC]【优化：与01背包相同】

#include
using namespace std;
int n,m;
long long v[3005],f[3005];
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)cin>>v[i];
    
    f[0]=1;
    
    for(int i=1;i<=n;i++)
    {
        for(int j=v[i];j<=m;j++)
        {
            f[j]=f[j]+f[j-v[i]];
        }
    }
    
    cout<<f[m]<<endl;
    
}

AcWing 532. 货币系统 （上一题拓展）

在网友的国度中共有 n 种不同面额的货币，第 i 种货币的面额为 a[i]，你可以假设每一种货币都有无穷多张。

为了方便，我们把货币种数为 n、面额数组为 a[1…n] 的货币系统记作 (n,a)。

在一个完善的货币系统中，每一个非负整数的金额 x 都应该可以被表示出，即对每一个非负整数 x，都存在 n 个非负整数 t[i] 满足 a[i]×t[i] 的和为 x。

然而，在网友的国度中，货币系统可能是不完善的，即可能存在金额 x不能被该货币系统表示出。

例如在货币系统 n=3, a=[2,5,9] 中，金额 1,3 就无法被表示出来。

两个货币系统 (n,a) 和 (m,b) 是等价的，当且仅当对于任意非负整数 x，它要么均可以被两个货币系统表出，要么不能被其中任何一个表出。

现在网友们打算简化一下货币系统。

他们希望找到一个货币系统 (m,b)，满足 (m,b) 与原来的货币系统 (n,a) 等价，且 m尽可能的小。

他们希望你来协助完成这个艰巨的任务：找到最小的 m。
输入格式

输入文件的第一行包含一个整数 T，表示数据的组数。

接下来按照如下格式分别给出 T组数据。

每组数据的第一行包含一个正整数 n。

接下来一行包含 n个由空格隔开的正整数 a[i]。
输出格式

输出文件共有 T行，对于每组数据，输出一行一个正整数，表示所有与 (n,a) 等价的货币系统 (m,b) 中，最小的 m。
数据范围

1≤n≤100,
1≤a[i]≤25000,
1≤T≤20

输入样例：

2 
4 
3 19 10 6 
5 
11 29 13 19 17 

输出样例：

2
5

AC代码

//a[i]可以用a[1]--->a[i-1]表示，则a[i]是答案
//a[i]可以用a[1]--->a[i-1]表示，则a[i]不是答案

#include
using namespace std;

const int N=25000+10,M=110;
int a[M],f[N];
int n,m;
int main()
{
    int t;cin>>t;
    while(t--)
    {
        
    cin>>n;
    for(int i=1;i<=n;i++)cin>>a[i];
    
    sort(a+1,a+n+1);
    
    memset(f,0,sizeof f);
    f[0]=1;

    int res=0,maxv=a[n];
    for(int i=1;i<=n;i++)
    {
        if(f[a[i]]==0)res++;
        for(int j=0;j<=maxv;j++)
        {
            if(j>=a[i])
                f[j]=f[j]+f[j-a[i]];        
        }
    }
    
    cout<<res<<endl;
    
    }
}

AcWing 6. 多重背包问题 III（暂无）

有 N 种物品和一个容量是 V的背包。

第 i种物品最多有 si 件，每件体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。
输出最大价值。
输入格式

第一行两个整数，N，V(0

接下来有 N行，每行三个整数 vi,wi,si，用空格隔开，分别表示第 i种物品的体积、价值和数量。
输出格式

输出一个整数，表示最大价值。
数据范围

0 0 0

提示

本题考查多重背包的单调队列优化方法。
输入样例

4 5
1 2 3
2 4 1
3 4 3
4 5 2

输出样例：

10

AcWing 1019. 庆功会(多重背包1模板)

为了庆贺班级在校运动会上取得全校第一名成绩，班主任决定开一场庆功会，为此拨款购买奖品犒劳运动员。

期望拨款金额能购买最大价值的奖品，可以补充他们的精力和体力。
输入格式

第一行二个数n，m，其中n代表希望购买的奖品的种数，m表示拨款金额。

接下来n行，每行3个数，v、w、s，分别表示第I种奖品的价格、价值（价格与价值是不同的概念）和能购买的最大数量（买0件到s件均可）。
输出格式

一行：一个数，表示此次购买能获得的最大的价值（注意！不是价格）。
数据范围

n≤500,m≤6000,
v≤100,w≤1000,s≤10

输入样例：

5 1000
80 20 4
40 50 9
30 50 7
40 30 6
20 20 1

输出样例：

1040

AC代码：可以二进制优化（略）

//多重背包1直接用
#include
using namespace std;
const int N=6000+10;
int n,m;
int s[N],w[N],v[N];
int f[N][N];
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)cin>>v[i]>>w[i]>>s[i];
    
    for(int i=1;i<=n;i++)
    {
        for(int j=0;j<=m;j++)
        {
            for(int k=0;k<=s[i]&&j>=k*v[i];k++)
            {
                f[i][j]=max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);
            }
        }
    }
    cout<<f[n][m]<<endl;
}

AcWing 7. 混合背包问题 (01,完全，多重)

有 N 种物品和一个容量是 V的背包。

物品一共有三类：

第一类物品只能用1次（01背包）；
第二类物品可以用无限次（完全背包）；
第三类物品最多只能用 si 次（多重背包）；

每种体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。
输出最大价值。
输入格式

第一行两个整数，N，V，用空格隔开，分别表示物品种数和背包容积。

接下来有 N行，每行三个整数 vi,wi,si，用空格隔开，分别表示第 i种物品的体积、价值和数量。
si=−1表示第 i种物品只能用1次；
si=0表示第 i种物品可以用无限次；
si>0表示第 i 种物品可以使用 si 次；

输出格式

输出一个整数，表示最大价值。
数据范围

0 0 −1≤si≤1000

输入样例

4 5
1 2 -1
2 4 1
3 4 0
4 5 2

输出样例：

8

一维[AC]

#include
using namespace std;
const int N=1010;
int n,m,f[N];
int v[N],w[N],s[N];
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)cin>>v[i]>>w[i]>>s[i];
    
    
    for(int i=1;i<=n;i++)//-------------------------------------物品数量
    {
        if(s[i]==0)//完全背包【小-->大】
        {
            for(int j=v[i];j<=m;j++)//------------------------------容量
                f[j]=max(f[j],f[j-v[i]]+w[i]);
        }
        else//01+多重背包--->二进制优化-->01【大-->小】
        {
            if(s[i]==-1)s[i]=1;//01
            else s[i]=s[i];//多重背包
            
            //二进制优化
            for(int k=1;k<=s[i];k=2*k)
            {
                for(int j=m;j>=k*v[i];j--)//------------------------------容量
                {
                    f[j]=max(f[j],f[j-k*v[i]]+k*w[i]);
                }
                s[i]=s[i]-k;
            }
            
            if(s[i]>0)
            {
                for(int j=m;j>=s[i]*v[i];j--)//------------------------------容量
                    f[j]=max(f[j],f[j-s[i]*v[i]]+s[i]*w[i]);
            }
        }
    }
    
    cout<<f[m]<<endl;
}

AcWing 8. 二维费用的背包问题（二维费用的01背包）

有 N 件物品和一个容量是 V 的背包，背包能承受的最大重量是 M。

每件物品只能用一次。体积是 vi，重量是 mi，价值是 wi。

求解将哪些物品装入背包，可使物品总体积不超过背包容量，总重量不超过背包可承受的最大重量，且价值总和最大。
输出最大价值。
输入格式

第一行三个整数，N,V,M，用空格隔开，分别表示物品件数、背包容积和背包可承受的最大重量。

接下来有 N行，每行三个整数 vi,mi,wi，用空格隔开，分别表示第 i件物品的体积、重量和价值。
输出格式

输出一个整数，表示最大价值。
数据范围

0 0 0 0

输入样例

4 5 6
1 2 3
2 4 4
3 4 5
4 5 6

输出样例：

8

三维/二维【优化：与01背包相同】

#include
using namespace std;
const int N=1010,M=110;
int f[N][M][M],cost1[N],cost2[N],w[N];
int n,V1,V2;

int main()
{
    cin>>n>>V1>>V2;
    for(int i=1;i<=n;i++)cin>>cost1[i]>>cost2[i]>>w[i];
    
    //三维
    for(int i=1;i<=n;i++)//物品数量
    {
        for(int v1=1;v1<=V1;v1++)//花费1
        {
            for(int v2=1;v2<=V2;v2++)//花费2
            {
                f[i][v1][v2]=f[i-1][v1][v2];//0
                if(v1>=cost1[i]&&v2>=cost2[i])
                    f[i][v1][v2]=max(f[i][v1][v2],f[i-1][v1-cost1[i]][v2-cost2[i]]+w[i]);//1
            }
        }
    }
    cout<<f[n][V1][V2]<<endl;   
}

#include
using namespace std;
const int N=1010,M=110;
int f[M][M],cost1[N],cost2[N],w[N];
int n,V1,V2;

int main()
{
    cin>>n>>V1>>V2;
    for(int i=1;i<=n;i++)cin>>cost1[i]>>cost2[i]>>w[i];
    
 
    //二维
    for(int i=1;i<=n;i++)//物品数量
    {
        for(int v1=V1;v1>=cost1[i];v1--)//花费1
        {
            for(int v2=V2;v2>=cost2[i];v2--)//花费2
            {
                f[v1][v2]=max(f[v1][v2],f[v1-cost1[i]][v2-cost2[i]]+w[i]);
            }
        }
    }
    cout<<f[V1][V2]<<endl;
    
}

AcWing 1020. 潜水员（二维费用的01背包+不少于的问题）

潜水员为了潜水要使用特殊的装备。

他有一个带2种气体的气缸：一个为氧气，一个为氮气。

让潜水员下潜的深度需要各种数量的氧和氮。

潜水员有一定数量的气缸。

每个气缸都有重量和气体容量。

潜水员为了完成他的工作需要特定数量的氧和氮。

他完成工作所需气缸的总重的最低限度的是多少？

例如：潜水员有5个气缸。每行三个数字为：氧，氮的（升）量和气缸的重量：

3 36 120

10 25 129

5 50 250

1 45 130

4 20 119

如果潜水员需要5升的氧和60升的氮则总重最小为249（1，2或者4，5号气缸）。

你的任务就是计算潜水员为了完成他的工作需要的气缸的重量的最低值。
输入格式

第一行有2个整数 m，n。它们表示氧，氮各自需要的量。

第二行为整数 k表示气缸的个数。

此后的 k行，每行包括ai，bi，ci，3个整数。这些各自是：第 i个气缸里的氧和氮的容量及气缸重量。
输出格式

仅一行包含一个整数，为潜水员完成工作所需的气缸的重量总和的最低值。
数据范围

1≤m≤21,
1≤n≤79,
1≤k≤1000,
1≤ai≤21,
1≤bi≤79,
1≤ci≤800

输入样例：

5 60
5
3 36 120
10 25 129
5 50 250
1 45 130
4 20 119

输出样例：

249

三维（略）/二维

/*
物品个数枚举:  [1....k]
费用1       :  [0....n]
费用2       :  [0....m]
*/


//二维费用问题（二维/三维）：max  可以if(i>=cost1[i]&&i>=cost2[i])
//f[i][j][k]:表示前i个物品，一维费用<=i,二维费用<=j  的方案的最大值
//--->可以if(i>=cost1[i]&&i>=cost2[i])
//max-->可以优化f[i][j]

//潜水员（只有二维）:       min  不可以if(i>=cost1[i]&&i>=cost2[i]),即使剩余体积<物品体积 也可以取到
//f[i][j][k]:表示前i个物品，一维费用>=i,二维费用>=j  的方案的最小值
//--->不可以if(i>=cost1[i]&&i>=cost2[i])
//min-->可以优化f[i][j]


#include
using namespace std;

const int N=85,M=25,K=1010;
int o2[K],n2[K],w[K];
int f[N][M];//氮气n，氧气m
int n,m,k;

int main()
{
    
    cin>>m>>n>>k;//氮气n，氧气m，商品数量
    
    for(int i=1;i<=k;i++)cin>>o2[i]>>n2[i]>>w[i];
    
    //初始化
    memset(f,0x3f,sizeof f);
    f[0][0]=0;
    
    
    //为什么从n-->0  m-->0
    //eg:f[3][5]:前i个物品，一维费用>=3,二维费用>=5的方案
    //现有物品: 4 4 w
    //虽然4>3,但是可以选择4这个物品,多余1而已
    //即f[-1][1]，即f[0][1]--->表示前i个物品，一维费用>=0,二维费用>=1的方案
    for(int i=1;i<=k;i++)
        for(int j=n;j>=0;j--)//一维氮气
            for(int l=m;l>=0;l--)//二维氧气
                f[j][l]=min(f[j][l],f[max(0,j-n2[i])][max(0,l-o2[i])]+w[i]);
    
    cout<<f[n][m]<<endl;
    
}

AcWing 1013. 机器分配 (分组背包+具体方案输出)

总公司拥有M台 相同 的高效设备，准备分给下属的N个分公司。

各分公司若获得这些设备，可以为国家提供一定的盈利。盈利与分配的设备数量有关。

问：如何分配这M台设备才能使国家得到的盈利最大？

求出最大盈利值。

分配原则：每个公司有权获得任意数目的设备，但总台数不超过设备数M。
输入格式

第一行有两个数，第一个数是分公司数N，第二个数是设备台数M；

接下来是一个N*M的矩阵，矩阵中的第 i 行第 j 列的整数表示第 i 个公司分配 j 台机器时的盈利。
输出格式

第一行输出最大盈利值；

接下N行，每行有2个数，即分公司编号和该分公司获得设备台数。

答案不唯一，输出任意合法方案即可。
数据范围

1≤N≤10,
1≤M≤15

输入样例：

3 3
30 40 50
20 30 50
20 25 30

输出样例：

70
1 1
2 1
3 1

二维[AC]

//分组

//n-->1 求f[i][j]
//1-->n 输出方案

#include
using namespace std;
const int N=1010;
int f[N][N];
int w[N],v[N];
int n,m;
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)cin>>v[i]>>w[i];
    
    //为什么从n-->1
    //原分析：从前向后
    //该做法是从n-->1选择物品(由递推公式得到)-------->不符合字典序
    //f[i][j]==f[i-1][j]         不选i   
    //f[i][j]==f[i-1][j-v]+w      选i
//------------------------分析分割线---------------------
    //如果是：从后向前
    //该做法是从1-->n选择物品(由递推公式得到)-------->符合字典序
    //f[i][j]==f[i+1][j]         不选i   
    //f[i][j]==f[i+1][j-v]+w      选i
    
    for(int i=n;i>=1;i--)
    {
        for(int j=0;j<=m;j++)
        {
            f[i][j]=f[i+1][j];
            if(j>=v[i])f[i][j]=max(f[i][j],f[i+1][j-v[i]]+w[i]);
        }
    }
    
    //最大值f[1][m]
    int j=m;
    for(int i=1;i<=n;i++)
    {
        //f[i][j]=max(不选，选)
        //f[i][j]=max(f[i+1][j],f[i+1][j-v[i]]+w[i])
        //if(f[i+1][j-v[i]]+w[i]>=f[i+1][j])--->选      保证字典序
        //else --->不选
        
        //选
        if(j>=v[i]&&f[i+1][j-v[i]]+w[i]>=f[i+1][j])
        {
            cout<<i<<" ";
            j=j-v[i];
        }
        //不选
        else 
        {
            
        }
    }
}

AcWing 426. 开心的金明 （01背包模板）

金明今天很开心，家里购置的新房就要领钥匙了，新房里有一间他自己专用的很宽敞的房间。

更让他高兴的是，妈妈昨天对他说：“你的房间需要购买哪些物品，怎么布置，你说了算，只要不超过 N元钱就行”。

今天一早金明就开始做预算，但是他想买的东西太多了，肯定会超过妈妈限定的 N元。

于是，他把每件物品规定了一个重要度，分为 5
等：用整数 1∼5 表示，第 5等最重要。

他还从因特网上查到了每件物品的价格（都是整数元）。

他希望在不超过 N元（可以等于 N元）的前提下，使每件物品的价格与重要度的乘积的总和最大。

设第 j件物品的价格为 v[j]，重要度为 w[j]，共选中了 k 件物品，编号依次为 j1，j2，…，jk，则所求的总和为：

v[j1]×w[j1]+v[j2]×w[j2]+…+v[jk]×w[jk]

请你帮助金明设计一个满足要求的购物单。
输入格式
输入文件的第 1行，为两个正整数 N 和 m，用一个空格隔开。（其中 N 表示总钱数，m为希望购买物品的个数）

从第 2行到第 m+1 行，第 j 行给出了编号为 j−1 的物品的基本数据，每行有 2 个非负整数 v 和 p。（其中 v 表示该物品的价格，p表示该物品的重要度）
输出格式

输出文件只有一个正整数，为不超过总钱数的物品的价格与重要度乘积的总和的最大值（数据保证结果不超过 108）。
数据范围

1≤N<30000,
1≤m<25,
0≤v≤10000,
1≤p≤5

输入样例：

1000 5
800 2
400 5
300 5
400 3
200 2

输出样例：

3900

二维/一维[AC]【优化：与01背包相同】

#include
using namespace std;
const int N=30000+10,M=30;
int w[N],v[N],f[N];
int n,m;
int main()
{
    cin>>m>>n;
    for(int i=1;i<=n;i++)cin>>v[i]>>w[i];
    
    
    for(int i=1;i<=n;i++)
    {
        for(int j=m;j>=v[i];j--)
        {
            f[j]=max(f[j],f[j-v[i]]+v[i]*w[i]);
        }
    }
    cout<<f[m]<<endl;
}

/*
//01
#include
using namespace std;
const int N=30000+10,M=30;
int w[N],v[N],f[M][N];
int n,m;
int main()
{
    cin>>m>>n;
    for(int i=1;i<=n;i++)cin>>v[i]>>w[i];
    
    
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            f[i][j]=f[i-1][j];
            if(j>=v[i])f[i][j]=max(f[i][j],f[i-1][j-v[i]]+v[i]*w[i]);
        }
    }
    cout<

AcWing 10. 有依赖的背包问题(暂无)

有 N 个物品和一个容量是 V的背包。

物品之间具有依赖关系，且依赖关系组成一棵树的形状。如果选择一个物品，则必须选择它的父节点。

如下图所示：
QQ图片20181018170337.png

如果选择物品5，则必须选择物品1和2。这是因为2是5的父节点，1是2的父节点。

每件物品的编号是 i，体积是 vi，价值是 wi，依赖的父节点编号是 pi。物品的下标范围是 1…N。

求解将哪些物品装入背包，可使物品总体积不超过背包容量，且总价值最大。

输出最大价值。
输入格式

第一行有两个整数 N，V，用空格隔开，分别表示物品个数和背包容量。

接下来有 N
行数据，每行数据表示一个物品。
第 i 行有三个整数 vi,wi,pi，用空格隔开，分别表示物品的体积、价值和依赖的物品编号。
如果 pi=−1，表示根节点。 数据保证所有物品构成一棵树。
输出格式

输出一个整数，表示最大价值。
数据范围

1≤N,V≤100

1≤vi,wi≤100

父节点编号范围：
内部结点：1≤pi≤N;
根节点 pi=−1;

输入样例

5 7
2 3 -1
2 2 1
3 5 1
4 7 2
3 6 2

输出样例：

11

AcWing 11. 背包问题求方案数 (最优选法的方案数)

有 N 件物品和一个容量是 V
的背包。每件物品只能使用一次。

第 i件物品的体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。

输出 最优选法的方案数。注意答案可能很大，请输出答案模 109+7的结果。
输入格式

第一行两个整数，N，V，用空格隔开，分别表示物品数量和背包容积。

接下来有 N行，每行两个整数 vi,wi，用空格隔开，分别表示第 i件物品的体积和价值。
输出格式

输出一个整数，表示 方案数 模 109+7的结果。
数据范围

0

0

输入样例

4 5
1 2
2 4
3 4
4 6

输出样例：

2

定义：恰好

//=恰好
#include 
#include 

using namespace std;

const int N = 1010, mod = 1e9 + 7;

int n, m;
int f[N],g[N];
int v[N],w[N];
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)cin>>v[i]>>w[i];
    
    
    memset(f,-0x3f,sizeof f);
    f[0]=0;
    g[0]=1;
    for(int i=1;i<=n;i++)
    {
        for(int j=m;j>=v[i];j--)
        {
            int maxv=max(f[j],f[j-v[i]]+w[i]);
            
            int s=0;
            if(f[j]==maxv&&f[j-v[i]]+w[i]!=maxv)s=g[j]%mod;
            if(f[j]!=maxv&&f[j-v[i]]+w[i]==maxv)s=g[j-v[i]]%mod;
            if(f[j]==maxv&&f[j-v[i]]+w[i]==maxv)s=(g[j]+g[j-v[i]])%mod;
            
            f[j]=maxv;
            g[j]=s;
         
        }
    }
    
    //因为定义==恰好&&求max==
    //所以f[j]可能不会恰好j，此时f[j]=0xcf
    //只有恰好j的才有意义,f[j]
    //因此需要求出最大值
    int res=0;
    for(int j=0;j<=m;j++)
        if(f[j]>f[res])
            res=j;
            
    int cnt=0;
    for(int j=0;j<=m;j++)
        if(f[res]==f[j])
            cnt=(cnt+g[j])%mod;
     
    cout<<cnt<<endl;
}

定义：不大于

//<=不超过
#include 
#include 

using namespace std;

const int N = 1010, mod = 1e9 + 7;

int n, m;
int f[N],g[N];
int v[N],w[N];
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)cin>>v[i]>>w[i];
    
    g[0]=1;
    for(int i=1;i<=n;i++)
    {
        for(int j=m;j>=v[i];j--)
        {
            int maxv=max(f[j],f[j-v[i]]+w[i]);
            
            int s=0;
            if(f[j]==maxv&&f[j-v[i]]+w[i]!=maxv)s=g[j]%mod;
            if(f[j]!=maxv&&f[j-v[i]]+w[i]==maxv)s=g[j-v[i]]%mod;
            if(f[j]==maxv&&f[j-v[i]]+w[i]==maxv)s=(g[j]+g[j-v[i]])%mod;
            
            f[j]=maxv;
            g[j]=s;
         
        }
    }
    //f[m]就是最大值
    int cnt=0;
    for(int j=0;j<=m;j++)
        if(f[m]==f[j])
            cnt=(cnt+g[j])%mod;
     
    cout<<cnt<<endl;
}

AcWing 12. 背包问题求具体方案(字典序最小的具体方案输出)

有 N 件物品和一个容量是 V的背包。每件物品只能使用一次。

第 i件物品的体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。

输出 字典序最小的方案。这里的字典序是指：所选物品的编号所构成的序列。物品的编号范围是 1…N。
输入格式

第一行两个整数，N，V，用空格隔开，分别表示物品数量和背包容积。

接下来有 N行，每行两个整数 vi,wi，用空格隔开，分别表示第 i件物品的体积和价值。
输出格式

输出一行，包含若干个用空格隔开的整数，表示最优解中所选物品的编号序列，且该编号序列的字典序最小。

物品编号范围是 1…N。
数据范围

0

0

输入样例

4 5
1 2
2 4
3 4
4 6

输出样例：

1 4

二维[AC]

//01

//n-->1 求f[i][j]
//1-->n 输出方案

#include
using namespace std;
const int N=1010;
int f[N][N];
int w[N],v[N];
int n,m;
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)cin>>v[i]>>w[i];
    
    //为什么从n-->1
    //原分析：从前向后
    //该做法是从n-->1选择物品(由递推公式得到)-------->不符合字典序
    //f[i][j]==f[i-1][j]         不选i   
    //f[i][j]==f[i-1][j-v]+w      选i
//------------------------分析分割线---------------------
    //如果是：从后向前
    //该做法是从1-->n选择物品(由递推公式得到)-------->符合字典序
    //f[i][j]==f[i+1][j]         不选i   
    //f[i][j]==f[i+1][j-v]+w      选i
    
    for(int i=n;i>=1;i--)
    {
        for(int j=0;j<=m;j++)
        {
            f[i][j]=f[i+1][j];
            if(j>=v[i])f[i][j]=max(f[i][j],f[i+1][j-v[i]]+w[i]);
        }
    }
    
    //最大值f[1][m]
    int j=m;
    for(int i=1;i<=n;i++)
    {
        //f[i][j]=max(不选，选)
        //f[i][j]=max(f[i+1][j],f[i+1][j-v[i]]+w[i])
        //if(f[i+1][j-v[i]]+w[i]>=f[i+1][j])--->选      保证字典序
        //else --->不选
        
        //选
        //总结：f[i][j]==f[i+1][j-v[i]]+w[i]就必须选
        if(j>=v[i]&&f[i][j]==f[i+1][j-v[i]]+w[i])
        {
            cout<<i<<" ";
            j=j-v[i];
        }
        //不选
        else 
        {
            
        }
    }
}

AcWing 734. 能量石 （暂无）

岩石怪物杜达生活在魔法森林中，他在午餐时收集了 N块能量石准备开吃。

由于他的嘴很小，所以一次只能吃一块能量石。
能量石很硬，吃完需要花不少时间。

吃完第 i块能量石需要花费的时间为 Si秒。

杜达靠吃能量石来获取能量。

不同的能量石包含的能量可能不同。

此外，能量石会随着时间流逝逐渐失去能量。

第 i块能量石最初包含 Ei 单位的能量，并且每秒将失去 Li单位的能量。

当杜达开始吃一块能量石时，他就会立即获得该能量石所含的全部能量（无论实际吃完该石头需要多少时间）。

能量石中包含的能量最多降低至 0。

请问杜达通过吃能量石可以获得的最大能量是多少？
输入格式

第一行包含整数 T，表示共有 T组测试数据。

每组数据第一行包含整数 N，表示能量石的数量。

接下来 N行，每行包含三个整数 Si,Ei,Li。
输出格式

每组数据输出一个结果，每个结果占一行。

结果表示为 Case #x: y，其中 x是组别编号（从 1 开始），y
是可以获得的最大能量值。
数据范围

1≤T≤10,
1≤N≤100,
1≤Si≤100,
1≤Ei≤105,
0≤Li≤105

输入样例：

3
4
20 10 1
5 30 5
100 30 1
5 80 60
3
10 4 1000
10 3 1000
10 8 1000
2
12 300 50
5 200 0

输出样例：

Case #1: 105
Case #2: 8
Case #3: 500

样例解释

在样例＃1中，有 N=4个宝石。杜达可以选择的一个吃石头顺序是：
吃第四块石头。这需要 5秒，并给他 80单位的能量。
吃第二块石头。这需要 5秒，并给他 5 单位的能量（第二块石头开始时具有 30 单位能量，5 秒后失去了 25单位的能量）。
吃第三块石头。这需要 100秒，并给他 20 单位的能量（第三块石头开始时具有 30 单位能量，10 秒后失去了 10单位的能量）。
吃第一块石头。这需要 20秒，并给他 0 单位的能量（第一块石头以 10 单位能量开始，110秒后已经失去了所有的能量）。

他一共获得了 105单位的能量，这是能获得的最大值，所以答案是 105。

在样本案例＃2中，有 N=3个宝石。

无论杜达选择吃哪块石头，剩下的两个石头的能量都会耗光。

所以他应该吃第三块石头，给他提供 8单位的能量。

在样本案例＃3中，有 N=2个宝石。杜达可以：吃第一块石头。这需要 12秒，并给他 300单位的能量。
吃第二块石头。这需要 5秒，并给他 200单位的能量（第二块石头随着时间的推移不会失去任何能量！）。

所以答案是 500。

AcWing 487. 金明的预算方案（暂无）

金明今天很开心，家里购置的新房就要领钥匙了，新房里有一间金明自己专用的很宽敞的房间。

更让他高兴的是，妈妈昨天对他说：“你的房间需要购买哪些物品，怎么布置，你说了算，只要不超过N元钱就行”。

今天一早，金明就开始做预算了，他把想买的物品分为两类：主件与附件，附件是从属于某个主件的，下表就是一些主件与附件的例子：

QQ截图20190313024710.png

如果要买归类为附件的物品，必须先买该附件所属的主件。
每个主件可以有0个、1个或2个附件。
附件不再有从属于自己的附件。

金明想买的东西很多，肯定会超过妈妈限定的N元。
于是，他把每件物品规定了一个重要度，分为5等：用整数1~5表示，第5等最重要。
他还从因特网上查到了每件物品的价格（都是10元的整数倍）。

他希望在不超过N元（可以等于N元）的前提下，使每件物品的价格与重要度的乘积的总和最大。

设第j件物品的价格为v[j]，重要度为w[j]，共选中了k件物品，编号依次为j1，j2，…，jk，则所求的总和为：
v[j1]∗w[j1]+v[j2]∗w[j2]+…+v[jk]∗w[jk]（其中*为乘号）

请你帮助金明设计一个满足要求的购物单。
输入格式

输入文件的第1行，为两个正整数，用一个空格隔开：N m，其中N表示总钱数，m为希望购买物品的个数。

从第2行到第m+1行，第j行给出了编号为j-1的物品的基本数据，每行有3个非负整数v p q，其中v表示该物品的价格，p表示该物品的重要度（1~5），q表示该物品是主件还是附件。

如果q=0，表示该物品为主件，如果q>0，表示该物品为附件，q是所属主件的编号。
输出格式

输出文件只有一个正整数，为不超过总钱数的物品的价格与重要度乘积的总和的最大值（<200000）。
数据范围

N<32000,m<60,v<10000

输入样例：

1000 5
800 2 0
400 5 1
300 5 1
400 3 0
500 2 0

输出样例：

2200

01背包问题
完全背包问题
多重背包问题 I
多重背包问题 II
多重背包问题 III
混合背包问题
二维费用的背包问题
分组背包问题
有依赖的背包问题
背包问题求方案数
背包问题求具体方案