路径规划算法简介

路径规划算法简介

1.涉及问题：

这里的路径规划是指如何寻找一条从给定起点到终点的路径，使机器人沿该路径移动的过程中不与障碍物发生碰撞且路程最短或移动代价最小。

2.简要介绍的算法：

1.遗传算法；
2.模拟退火；
3.人工势场；
4.蚁群算法；
5.RRT;
6.PRM;
7.Dijkstra;
8.A
9.Field D****

遗传算法
遗传算法（Genetic Algorithm）是一类借鉴生物界的进化规律（适者生存，优胜劣汰遗传机制）演化而来的随机化搜索方法。它是由美国的J.Holland教授1975年首先提出，其主要特点是直接对结构对象进行操作，不存在求导和函数连续性的限定；具有较好的全局寻优能力；采用概率化的寻优方法，能自动获取和指导优化的搜索空间，自适应地调整搜索方向，不需要确定的规则。遗传算法的这些性质，已被人们广泛地应用于组合优化、机器学习、信号处理、自适应控制和人工生命等领域。就遗传算法运用于路径规划而言，可简单概括为如下步骤：1随机选取节点组成一组初始路径群（即许多条路径构成的集合）；2求出路径群中每条路径的路径长度；3选择路径群中任意两条路径进行交叉和变异，路径长度越短的路径有更高的被选择的概率，继续选择然后进行交叉和变异形成新的子代路径群；4按照路径长度淘汰掉初始路径群和子代路径群中路径较长的路径，然后形成新的路径群；5回到步骤1继续下一轮迭代，制定迭代到达一定次数或路径长度变化非常缓慢的情况时停止迭代，此时路径群中最短的路径即为遗传算法求得的优化路径。
模拟退火
模拟退火是S. Kirkpatrick, C. D. Gelatt和M. P. Vecchi在1983年提出。模拟退火算法（Simulated Annealing），简称SA，是一种适用于大规模组合优化问题的有效近似算法。它模仿固体物质的退火过程，通过设定初温、初态和降温率控制温度的不断下降，结合概率突跳特性，利用解空间的邻域结构进行随机搜索。具有描述简单、使用灵活、运行效率高、初始条件限制少等优点，但存在着收敛速度慢、随机性等缺陷，参数设定是应用过程中的关键环节。应用于路径规划问题中可简单描述其运行步骤如下：1.进行若干次的随机选择路径，从中选择出路径长度最小的路径作为模拟退火迭代方法的初始解；2.对初始路径进行随机的元素置换然后依据Metropolis准则判断转换后的新解是否可以被接受；3重复步骤2直至Metropolis准则中定义的温度系数T低到一定程度后停止迭代，此时当前解即为模拟退火法求得的最优路径。关于Metropolis准则可简单概括如下式：

上式(3.1)中i为当前状态，Ei和Ej分别代表i状态和j状态的温度，ε为0 到1间的随机数。
通过上面分析可以看出其实遗传算法和模拟退火算法有许多类似的地方，它们都是通过随机抽样的办法在解空间中选取可能的解然后按照评估函数进行解的评价，关键不同点在于遗传算法通过建立一个比较庞大的解的群（集合），并用这个群不断进行迭代从而保证其不易陷入局部最优解。相对而言模拟退火算法虽然仅用一个样本（或者称一个解）进行迭代，但是其引入Metropolis准则从而避免在抽样过程中陷入局部最优解这也正是模拟退火算法的核心所在。

人工势场法
人工势场法路径规划是由Khatib提出的一种虚拟力法（Oussama Khatib，Real-Time obstacle Avoidance for Manipulators and Mobile Robots）。它的基本思想是将机器人在周围环境中的运动，设计成一种抽象的人造引力场中的运动。人工势场包括引力场合斥力场，其中目标点对物体产生引力，引导物体朝向其运动（这一点有点类似于A*算法中的启发函数）。障碍物对物体产生斥力，避免物体与之发生碰撞。物体在路径上每一点所受的合力等于这一点所有斥力和引力的和。对于二维平面里面路径规划的问题，人工势场法就如同在这个二维平面内建立起一个三维的势场，机器人不断从势能高（位置高）的地方向势能低（位置低）的地方移动，直至到达最低的地方。应用势场法规划出来的路径一般是比较平滑并且安全，但是这种方法存在局部最优点问题。同时，当物体离目标点比较远时，引力将变的特别大，相对较小的斥力在甚至可以忽略的情况下，物体路径上可能会碰到障碍物；其次当目标点附近有障碍物时，斥力将非常大，引力相对较小，物体很难到达目标点；最后，在某个点，引力和斥力刚好大小相等，方向想反，则物体容易陷入局部最优解或震荡。

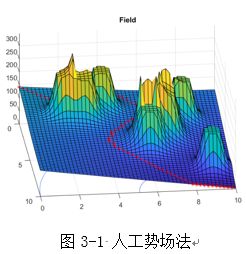
（上图来源于互联网）
蚁群算法
蚁群算法是受到对真实蚂蚁群觅食行为研究的启发而提出。生物学研究表明：一群相互协作的蚂蚁能够找到食物和巢穴之间的最短路径,而单只蚂蚁则不能。生物学家经过大量细致观察研究发现,蚂蚁个体之间的行为是相互作用相互影响的。蚂蚁在运动过程中,能够在它所经过的路径上留下一种称之为信息素的物质,而此物质恰恰是蚂蚁个体之间信息传递交流的载体。蚂蚁在运动时能够感知这种物质,并且习惯于追踪此物质爬行,当然爬行过程中还会释放信息素。一条路上的信息素踪迹越浓,其它蚂蚁将以越高的概率跟随爬行此路径,从而该路径上的信息素踪迹会被加强,因此,由大量蚂蚁组成的蚁群的集体行为便表现出一种信息正反馈现象。某一路径上走过的蚂蚁越多,则后来者选择该路径的可能性就越大。蚂蚁个体之间就是通过这种间接的通信机制实现协同搜索最短路径的目标的。

RRT
快速扩展随机树（RRT / rapidly exploring random tree）的路径规划算法是通过对状态空间中的随机选取的采样点进行碰撞检测，避免了相对复杂的对空间的建模，能够有效地解决高维空间和复杂约束的路径规划问题。它以一个初始点作为根节点，通过随机采样增加叶子节点的方式，生成一个随机扩展树，当随机树中的叶子节点包含了目标点或进入了目标区域，便可以在随机树中找到一条由从初始点到目标点的路径。该方法的特点是能够快速有效地搜索高维空间，通过状态空间的随机采样点，把搜索导向空白区域，从而寻找到一条从起始点到目标点的规划路径，适合解决多自由度机器人在复杂环境下和动态环境中的路径规划。

PRM（Probabilistic Roadmap）是一种基于图搜索的方法。算法主要思想是将连续空间转换成离散空间，即在给定图的自由空间里随机撒点（自定义个数），构建一个路径网格图，然后在利用A*等搜索算法 在路线图上寻找路径，以提高搜索效率。这种方法能用相对少的随机采样点来找到一个解，对多数问题而言，相对少的样本足以覆盖大部分可行的空间，并且找到路径的概率为1（随着采样数增加，P（找到一条路径）指数的趋向于1）。显然，当采样点太少，或者分布不合理时，PRM算法是不完备的，但是随着采用点的增加，也可以达到完备。所以PRM是概率完备且不最优的。

Dijkstra
迪科斯彻（Dijkstra）算法是由荷兰计算机科学家艾兹格•W•迪科斯彻 （Edsger Wybe Dijkstra）于1959 年提出的。Dijkstra算法从地图上设定的起点开始进行算法的初始化，并建立一个特殊的节点集合（这个集合的大小是动态的），这里暂且把这个集合记着Set-f（fringe）。在初始化的最后再建立一个与地图上节点矩阵大小一样的矩阵P，用于存放与地图矩阵上同样（索引）位置节点的父节点的索引（这个父节点的索引在下面会提到）。在算法的第一次迭代中将起点的路径信息传递给与起点相邻的节点，就网状的地图而言相当于将路径信息传递给与起点存在直接路径的节点，对于二维平面里面的Y-X轴状栅格地图而言即试图将路径信息传递给与其相邻的8个节点（当起点不位于地图边界上）。这里所谓传递路径信息主要是指，被传递路径信息节点到地图起点的路径长度。在第一次迭代中将哪些被传递路径信息的节点插入到节点集合Set-f中，并且将这些被传递路径信息节点的父节点定义为传递路径信息的节点，即被传递路径信息节点在P矩阵中的索引位置上存放的数据是被传递路径信息节点父节点的索引。在进行下一次迭代时，则是从集合Set-f中选取距离起点路径长度最短的节点作为本次迭代过程中传递路径信息的起点，待传递路径信息的起点被选定后即可将路径信息传递给与传递路径信息节点相邻的节点（当然这些与传递路径信息节点相邻的节点中已经曾经作为过传递路径信息起点的节点无需再被传递），同时在矩阵P中将被传递路径信息节点的父节点更新为传递路径信息的节点。在完成这样的路径信息传递后需要将向上面这样周而复始地进行传递，最终直至路径信息被传递到路径的终点时结束迭代。最后从路径的终点开始在矩阵P中进行向后的索引，即索引到某个节点的父节点，该父节点再索引其父节点直至索引到路径起点为止即可生成一条“最短的”的路径。将Dijkstra算法应用于二维平面内栅格地图上的算法伪码如下：
Procedure Calculate_estimate_value(i)
{01} Return line_distance(i,g);
Procedure Initialize()
{02}[r c]=size(Map);
{03} State=zeros(r,c);
{04} G=inf(r,c);
{05} P=inf(r,c);
{06} P(s)=s;
{07} Set-f=null;
{08} Set-f.insert(s,calculate_estimate_value(s));
Procedure Main()
{09} Initialize();
{10} While(State(g)≠closed )
{11} cv=Set-f.getMin();
{12} for all negh_cv∈ neighbor(cv)
{13} if(state(negh_cv) ≠closed )
{14} temp_esti=G(cv)+line_distance(negh_cv,cv)
{15} if(temp_esti {16} P(negh_cv)=cv;
{17} G(negh_cv)=temp_esti;
{18} state(negh_cv)=closed;
{19} Set-f.remove(cv);
{20} if(Is_empty(Set_f))
{21} break;
伪码第1行中函数line_distance(i,g)返回节点i到地图目标节点g(goal)间的直线距离。障碍物地图由矩阵Map表示。S表示路径起点，Set-f.getMin()用于反馈集合Set-f中距离起点路径长度最短的节点的索引。伪码12行中neighbor(cv)表示与节点cv相邻的节点组成的集合，在二维栅格地图上若cv节点不位于地图边界上时与其相邻的节点有且仅有8个。矩阵G用于存放节点距离地图上路径起点的路径长度。

上图3-4中标有S的方格代表地图上的起点，标有G的方格代表路径的目标点，即终点。图3-4中深黑色部分的方格代表地图上的障碍物，灰色部分的方格代表被算法计算区域，黄色部分方格代表在算法结束时该部分的方格仍然还在集合Set-f中，绿色部分方格表示算法搜索得到的路径。每个方格上的箭头均指向其父方格（或称算法中的节点）。每个方格的左下方的两组数据，由上至下分别表示该方格距离地图上起点的路径长度和该方格在Set-f中的评估数值，对于Dijkstra即为G值，对于A-Star即为F值。

A-Star(A)搜索算法*

A-Star(下称A*)算法的整体结构和Dijkstra基本一致，关键的地方在于A算法为提高算法向目标点搜索的能力，即避免一些不必要的搜索方向而引入启发函数使得搜索效率的到很大提高。在原有Dijkstra算法的中，当算法即将进行下一次迭代时，是从Set-f集合中选距离起点最近的节点(cv)作为即将进行的迭代过程中的传递路径信息的节点，即G(cv)满足下式：
G(cv)≤G(i) ∀ i ∈Set-f (3.2)
相比之下A仅是将Dijkstra算法中上式3.2变换成下式：
F(cv)≤F(i) ∀ i ∈Set-f (3.3)
上式(3.3)中：
F(i)=G(i)+H(i) (3.4)
式 (3.4)中G(i)依然为节点i到地图上路径起点的距离，而H(i)为节点i到地图上路径目标点的估计距离。H函数数值的大小通常可以由以下几类距离中的一类来计算， 曼哈顿距离(Manhattan distance) 、 切比雪夫距离(Chebyshev distance) 、 欧式距离(Euclidean distance)和Octile 距离 。
曼哈顿距离：
H(i) = (abs(i.x – g.x) + abs(i.y – g.y)) (3.5)
切比雪夫距离：
H(i) = Max(abs(i.x – g.x) ,abs(i.y – g.y)) (3.6)
欧式距离：
H(i) =(abs(i.x–g.x) + abs(i.y–g.y)) (3.7)
曼哈顿距离：
H(i) = sqrt((i.x–g.x)^2 +(i.y–g.y)^2) (3.8)
Octile 距离：
H=√2Min(abs(i.x – g.x),abs(i.y – g.y)+Max(abs(i.x – g.x) ,abs(i.y – g.y)) (3.9)
上式(3.5-3.9)中i.x表示点i的x轴坐标值，abs()为求取绝对值的函数。
图3-5 A算法中常见的几种估计距离
对比式(3.2)和(3.4)不难发现Dijkstra与A算法差别在于从Set-f中选择作为下一次迭代过程中使用的主动传递路径信息节点的方式不样。Dijkstra几乎是以起点为圆心在任何一个方向上都进行主动传递路径信息节点的选择，这样就导致路径信息最终几乎也是以起点为圆心逐渐向圆外进行拓展，没有明显的指向性。然而A算法在执行过程中Set-f中靠近路径起点与路径终点的节点将会被优先选取，这样就使得A算法在迭代过程中逐渐向路径终点靠近，从而明显提高算法的搜索效率。
Fieled D算法
Field D* 算法是由 Dave Ferguson 和Anthony Stentz提出的一种Any-Angle Path Planning algorithm算法（以下称无角度约束路径规划）。所谓无角度约束路径规划主要是指，许多路径规划算法在迭代过程中传递路径信息的方式是以主动传递路径信息的节点仅向其相邻的8个节点进行路径信息传递，而且在算法迭代过程中所有节点的父节点一定是与其相邻的某个节点，这样将导致算法最终得到的路径上转向点转过的角度一定是45°的倍数（对于横纵等间距的栅格地图）。如下图3-7所示这类有角度约束的算法生成的路径通常如图3-7(a)而无角度约束路径规划算法的目的是找到图3-7(b)中虚线的路径。图3-7中灰色方块代表地图上的障碍区域，Sstar和Sgoal分别代表地图上的起点和终点。

图3-6 受约束的路径规划和无角度约束路径规划
受到角度约束的路径规划算法中被传递路径节点的父节点一定是与其相邻的某个节点之一。

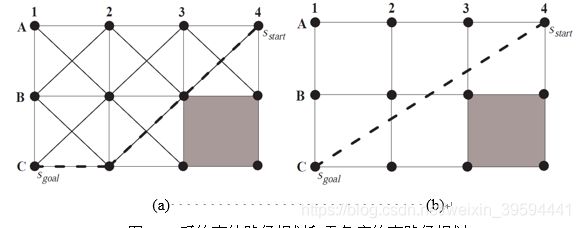
图3-7 受约束的路径规划和无角度约束路径规划

总的来说在计算静态地图时Field D算法的主体结构与3.3节中Dijkstra算法比较相似，主要区别在于Field D算法传递路径信息的方式。与存在角度约束的算法中通过节点向其相邻节点传递路径信息的方式不同，Field D算法是通过两个相邻节点向与这两个节点均相邻的节点传递路径信息。如下图3-8 (a)所示某时刻算法拟对节点s进行路径信息传递（即求出该点至地图上路径起点的距离），为确保节点s的路径长度最短，显然将s与路径起点进行直接连线（这里先假定这条直线不穿越障碍物）节点s可获得最短的距离，这样的连线必然穿越与s节点相邻的两个节点组成的连线。如图3-8 (a)所示由s点出发的箭头与S1和S2组成的线段相交。此时可抽象为S1和S2组成的线段向与S1和S2均相邻的节点S传递路径信息，具体计算S节点路径长度的方法可见图3-9中Field D算法计算路径信息（路径长度）的伪码。

图3-8 Field D*算法传递路径信息

分析下图3-9中伪码不难发现Field D算法，首先假定在节点Sa和Sb间的连线上距离起点的路径长度呈线性分布（这其实与地图上的实际情况差别比较大，也最终导致Field D算法不能准确地传递路径信息，因为只有很少的情况下才满足呈线性分布的关系）。

图3-9 Field D算法传递路径信息函数伪码
小结
通过分析不难发现对于在二维地图中设定起点和终点，寻找最短路径的问题，使用遗传算法和模拟退火算法不太恰当。这是因为这两种算法都是在已知且固定的解空间维度中搜索最优解，而显然对于寻找最短路径问题，组成最优解的节点的个数并不是确定的。人工市场法建模方法相对复杂，不恰当的建模方法容易引发算法震荡和陷入局部最优，而且在差异比较大的地图环境中使用同一套建模方法算法还有可能出现与障碍物相碰撞或震荡。蚁群算法虽然具有较好的搜索最优解的能力，但是它和A算法一样应用在二维栅格地图上时都存在搜索步长的约束，而无法实现无角度约束路径规划（Any-Angle Path Planning），而在求解最优路径的所花的时间上A算法相比于蚁群算法有非常大的优势。Field D算法是一种相对诞生比较早的无角度约束路径规划算法，虽然后面有涌现出其它的同类算法（Any-Angle Path Planning），例如Theta-star、Block A-star 和Incremental Phi-star，这些算法的运行效率或求解的最优路径相比Field D*并没有明显的提高。