斜率优化dp

斜率优化

引言

当你看到这一篇博客时，相信你已经对基本的$dp$模型有了了解，已经能独立推导出较为简单的$dp$式子，但有时在进行$dp$转移的过程，需要耗费较高的复杂度，朴素的$dp$方程及转移只能得到部分分数，无法取得AC，此时就需要如斜率优化这样来减少时间复杂度的工具。当然，斜率优化也只是一种工具，必须在可以推出正确但效率较低的$dp$式后才能发挥用处，故而$dp$的基本功才是关键。

斜率优化的难度体现在：在$OI$领域初步接触到与几何相关的应用，首次理解上稍困难，但在理解后，斜率优化的难度其实并不高，掌握套路就可以轻松运用。

基础斜率优化（双单调）

前文中提到，斜率优化是用来辅佐$dp$的，但也并不能辅佐所有的$dp$。能被斜率优化的$dp$非常典型，以一道题目为例：打印文章

给出 $N$ 个单词，每个单词有个非负权值 $C_i$，现要将它们分成连续的若干段，每段的代价为此段单词的权值和的平方，还要加一个常数 $M$，即 $(\sum C_i{)}^2+M$。现在想求出一种最优方案，使得总费用之和最小。

不难得出朴素$dp$做法：
设$f_i$为将前$i$个单词划分的最小费用，$sum{c}_i$表示$C_i$的前缀和
$f_i=mi{n}_{j=0}^{i-1}(f_j+(sum{c}_i-sum{c}_j{)}^2+M)$
（若无法理解朴素$dp$，建议先不要学习斜率优化）

在朴素$dp$的过程中，需要同时枚举$i,j$，复杂度为$n^2$，显然无法通过此题。

若只枚举$i$，我们只需要花较低的复杂度找到一个最优的$j$，即可以使$(f_j+sum{c}_i^2-2\times sum{c}_i\times sum{c}_j+sum{c}_j^2+M)$最小的$j$，找到之后转移即可，斜率优化正是来帮助我们快速地寻找到$j$

对于上式中的多项式，将其展开为多个单项式，即：
$f_i=mi{n}_{j=0}^{i-1}(f_j+sum{c}_i^2-2\times sum{c}_i\times sum{c}_j+sum{c}_j^2+M)$

对于式子中的常数项，无论$j$取何值，都需加上这一常数项，它对于寻找最优的$j$没有作用，因此在斜率优化的过程中，我们暂时不需考虑常数项。

现在将$min$删去，只考虑对于某一个处于范围$[0,i)$的$j$，则转移方程为：
$f_i=f_j+sum{c}_i^2-2\times sum{c}_i\times sum{c}_j+sum{c}_j^2$

在这个方程中，存在四类单项式：
1.只与$i$有关的，例如：$sum{c}_i^2,f_i$
2.只与$j$有关的，例如：$sum{c}_j^2,f_j$
3.与$i,j$都有关的，例如：$-2\times sum{c}_i\times sum{c}_j$

接下来进行移项
将只与$j$有关的移向左侧，其余移向右侧
整理两侧式子为这样的形式：
$f(j)=g(i)\ast h(j)+r(i)$
（$f(i)$即为只关于$i$的多项式，$g,h,r$同理）

上式则可以整理为：
$f_j+sum{c}_j^2=2\times sum{c}_i\times sum{c}_j+f_i-sum{c}_i^2$

初中我们学过一次函数的表达式$y=kx+b$，与我们所得到的方程相似

将$f_j+sum{c}_j^2$视为$y$：因变量
将$2\times sum{c}_i$视为$k$：斜率
将$sum{c}_j$视为$x$：自变量
将$f_i-sum{c}_i^2$视为$b$：截距

我们的最终目的是要找到最优的$j$，更直接的目的，就是让$f_i$尽可能的小，观察$f_i$在哪里？

没错，在截距中！

由于$j$的枚举范围是$[0,i)$，当我们计算$f_i$时，显然对于$\forall j\in [0,i)$，自变量$sum{c}_j$与因变量$f_j+sum{c}_j^2$均已知，已知$x,y$，则可以将其视为平面直角坐标系的一个定点，故此时在平面直角坐标系中已经存在了$i$个定点。

观察斜率，也是一个已知量，那么对于每一个$j$，我们就可以得到一条斜率为$2\times sum{c}_i$，且过点$(sum{c}_j,f_j+sum{c}_j^2)$的确定直线。直线确定，截距也就可以确定，进而$f_i$也可以确定。

由于枚举值为$i$，则斜率此时作为一个定值，也就是说，我们平移一条斜率为定值$2\times sum{c}_i$的直线，使其过某点$(sum{c}_j,f_j+sum{c}_j^2)$，就可以得到一个合法的$f_i$

那怎么在合法的$f_i$中找到最小的一个呢？

若对于每个点$(sum{c}_j,f_j+sum{c}_j^2)$，都计算出对应的$f_i$为多少，再取比较出最小的，显然复杂度仍未$n^2$，起不到优化的作用。

有没有什么办法可以不考虑所有点，换言之，有没有一些点绝不可能作为答案？这样我们无需枚举这些点，以减少时间复杂度

当然是有的，我们仍以此题为例，在本题中，$k\ge 0$且单调递增，$x\ge 0$且单调递增，假设在平面直角坐标系中存在三个点如图所示：

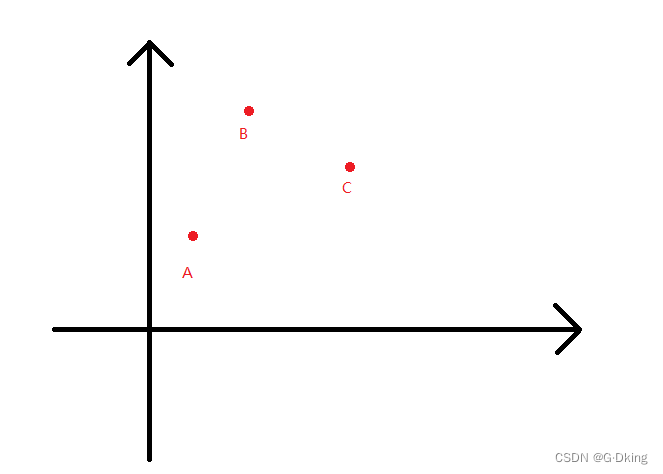
请试着拿一条斜率$\ge 0$的直线，观察这条直线过哪个点时，截距最小。

尝试后不难发现，当斜率$\in [0,k_{AC}]$时，$A$为最优点；当斜率$\in (k_{AC},+\infty )$时，$C$为最优点；无论何时，$B$都不会为最优点，而$B$则是刚才提到的绝不可能作为答案的点，可删除。

那么怎么筛选出形如$B$的所有无用点呢？我们以一个更大的图为例来考虑这个问题：

在这个图中，再次进行尝试，不难看出有用点只有$I,J,H,G$，其余均为无用点

将这四个点依次连接，如图所示：

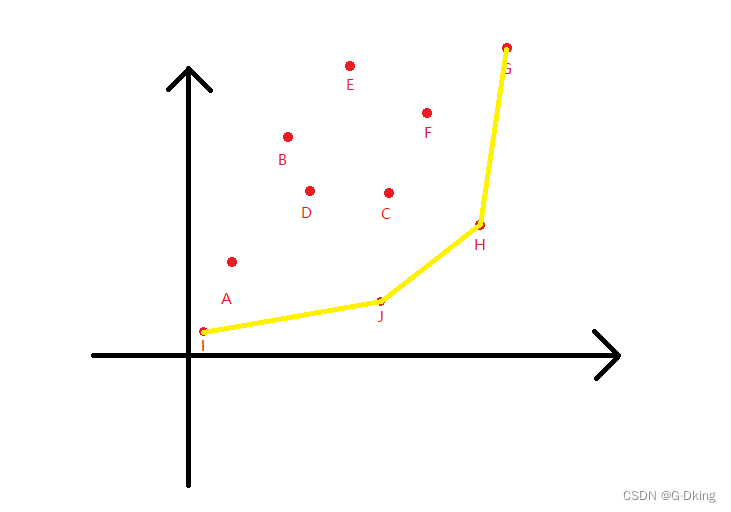
它们构成了一个向外凸的形状，我们将其称之为凸包或凸壳

由于它向外凸出，将一条斜率固定的直线从下向上平移，必然会与这个凸出的图形相切，无法到达凸包内部的点，故只有凸包上的点才为有效点

那么问题就转化为，如何找出这个凸壳？

已知$x$单调递增，即图中的所有点加入的顺序应该是以$x$从小到大的顺序排列的，顺序为：
$I,A,B,D,E,J,C,F,H,G$
我们来模拟一下凸包维护的过程

首先维护一个队列
将$I$插入队列
将$A$插入队列
判断插入$B$点后，$I,A,B$三点能否构成凸包
由于$k_{IA}>k_{AB}$，无法构成一个凸包，将$A$从队列中弹出
将$B$插入队列
判断插入$D$点后，$I,B,D$三点能否构成凸包
由于$k_{IB}>k_{BD}$，无法构成一个凸包，将$B$从队列中弹出
将$D$插入队列
判断插入$E$点后，$I,D,E$三点能否构成凸包
由于$k_{ID}<k_{DE}$，可以构成一个凸包
将$E$插入队列
判断插入$J$点后，$I,D,E,J$四点能否构成凸包，等价于判断$D,E,J$三点能否构成凸包
由于$k_{DE}>k_{EJ}$，无法构成一个凸包，将$E$从队列中弹出
判断$I,D,J$三点能否构成凸包
由于$k_{ID}>k_{DJ}$，无法构成一个凸包，将$D$从队列中弹出
将$J$插入队列
$...$

以这种方式：比较队列中 最后两点的斜率 与 队尾点和新点的斜率 大小，判断是否将队尾弹出，再将新点插入。

我们就可以将凸包成功维护出来。

有效点已经全部筛选出来了，接下来，就该去寻找最优点了。

可以很暴力的枚举每一个凸包上的点，取最小值作为答案，但仍存在更为优秀的一种做法：

仍以上图为例子：
当$k\in [0,k_{IJ]}$时，最优点为$I$
当$k\in (k_{IJ},k_{JH]}$时，最优点为$J$
当$k\in (k_{JH},k_{HG]}$时，最优点为$H$
当$k\in (k_{HG},+\infty )$时，最优点为$G$
由于$k$单调递增，
所以，若此时的最优点为$J$，则以后任意时刻的最优点都不再可能是$I$，$I$尽管在凸包上，也沦为了无用点。
在队列中，$I$身居队首，于是可以很轻易地将队首弹出即可
在弹出所有无效的队首之后，此时队首的点，即为最优点！
而这个过程，实际上也就是单调队列优化的过程。

至此，我们通过一个双端（单调）队列，既维护了凸包，又找到了最优点

时间复杂度：
首先枚举$i$需花费$O(n)$
在此循环中，我们在时刻的维护队列，每个点都最多只会进出队列一次，故总复杂度由$O(n^2)$降至$O(n)$

给一份本题的标程：

#include
using namespace std;
const int N=5e5+10;
int n,q[N];
long long m,c[N],sc[N],f[N];
long long X(int p){return sc[p];}
long long Y(int p){return f[p]+sc[p]*sc[p];}
long long K(int p){return 2ll*sc[p];}
int main()
{
	while(~scanf("%d%lld",&n,&m))
	{
		for(int i=1;i<=n;i++) scanf("%lld",&c[i]),sc[i]=sc[i-1]+c[i];
		int head=1,tail=1;
		q[1]=0;
		for(int i=1;i<=n;i++)
		{
			while(head<tail&&K(i)*(X(q[head+1])-X(q[head]))>=Y(q[head+1])-Y(q[head])) head++;
			int j=q[head];
			f[i]=f[j]+(sc[i]-sc[j])*(sc[i]-sc[j])+m;
			while(head<tail&&(Y(i)-Y(q[tail]))*(X(q[tail])-X(q[tail-1]))<=(Y(q[tail])-Y(q[tail-1]))*(X(i)-X(q[tail]))) tail--;
			q[++tail]=i;
		}
//		memset(f,0x3f,sizeof(f));
//		f[0]=0;
//		for(int i=1;i<=n;i++) for(int j=0;j
		printf("%lld\n",f[n]);	
	}
	return 0;
}

注意事项：
1.在计算斜率时，由于需要使用除法，存在精度问题，所以通过去分母，将式子转为乘法形式比较大小。
2.为了防止一些莫名其妙的麻烦，在比较斜率大小时需要写成$>=$和$<=$。
3.弹队首队尾时都为$while$循环
4.注意括号，不要括错！不要漏括号！

例题：

双单调斜率优化模型讨论

在这类题目模型中，有时并不是需要维护单调队列，而是需要维护单调栈
例如：柠檬
那么在什么时候需要维护单调队列，什么时候又需要维护单调栈呢？
下面将对这个问题进行讨论：

首先让我们来考虑一下凸包的形状，在上文例题中，凸包是向右下凸出的，思考如果我们不限制$k\ge 0$，那么凸包将是什么形状？

答案是这样：

凸包整体向下凸起

那有没有向上凸起的凸包呢？
当然有！
如果我们将斜率优化题目中所求改为求截距的最大值，那么凸包就会变成：

故影响凸包形状的，实际上是题目中所求的是最小值还是最大值。

接下来判断如何确定使用单调队列还是单调栈。
影响因素有三个：
1.凸包的形状
2.$k$的单调性
3.$x$的单调性

举一个例子：
$k,x$均单调递增，凸包下凸
即：

随着$k$的增大，最优决策点的移动方向是向右的，即向$x$增大的方向，于此同时$x$也在增大，向右移动，二者同向
所以需要维护一个队列，队首移动$k$，队尾移动$x$，同时向右移动
同理，当$k,x$均单调递减，凸包下凸时，也需要维护单调队列

当$k$单调递增，$x$单调递减呢？
此时二者移动方向相反，新插入的点实际上斜率更小，用栈维护，才能维护出斜率单调递增
同理可得$k$单调递减，$x$单调递增时，也需要用单调栈

对于上凸的情况请读者自行讨论，这里只给出结论：

当凸包下凸时，$k,x$单调性相同，使用单调队列，$k,x$单调性不同，使用单调栈；
当凸包上凸时，$k,x$单调性相同，使用单调栈，$k,x$单调性不同，使用单调队列。

k不单调，x单调的斜率优化

承接上文中，当我们维护出凸包后，我们可以枚举凸包上的每一个点，求最小值即为答案。
对此我们加以优化，用单调队列将复杂度降得更低，但此优化的前提是$k$单调递增
那如果$k$并不单调递增，我们只好另寻他路
实际上很简单：二分！
由于凸包中相邻两点的斜率具有单调性，所以可以二分找出最优点，以优化时间复杂度，将复杂度降至$nlogn$
例题：任务安排3

x不单调或x,k均不单调的斜率优化

由于插入点不再可以用队列这样的线性数据结构去维护，所以难度大大提高
常见的维护方法有：$CDQ$分治，平衡树，李超线段树

$CDQ$分治：
由于$x,k$均不单调，而我们的斜率优化需要让他们单调才可以进行，在$dp$的过程中只能将$[0,i)$的转移到$i$，在编号上又存在着一种单调性关系，同时需要维护三种单调性，很自然的可以想到解决三维偏序问题的$CDQ$分治。

1.将一个点所对应的$id,k,x$都提前预处理，存入结构体中
2.将结构体按照$k$值排序，处理第一维偏序（斜率）
3.进行$CDQ$分治，每次将区间划分为两部分，划分的方式采用将编号较小的一半放在左侧，编号较大的一半放在右侧，维护第二维偏序（编号）
4.$CDQ$分治递归左区间
5.将左侧按照$x$值排序，使左侧单调，此时由于右侧均未被递归，$k$值仍有序，构成了左侧$x$值单调，右侧$k$值单调，左侧的编号大小均小于右侧的编号大小
6.维护出左侧的所有点构成的凸包
7.用左侧维护出的凸包更新右侧的答案，由于右侧斜率单调，做法如同双单调型即可
8.$CDQ$分治递归右区间

例题：