模型压缩之知识蒸馏
![]()
1. 介绍
1.2 背景
虽然在一般情况下,我们不会去区分训练和部署使用的模型,但是训练和部署之间存在着一定的不一致性:
在训练过程中,我们需要使用复杂的模型,大量的计算资源,以便从非常大、高度冗余的数据集中提取出信息。在实验中,效果最好的模型往往规模很大,甚至由多个模型集成得到。而大模型不方便部署到服务中去,常见的瓶颈如下:
- 推断速度慢
- 对部署资源要求高(内存,显存等)
在部署时,我们对延迟以及计算资源都有着严格的限制。
因此,模型压缩(在保证性能的前提下减少模型的参数量)成为了一个重要的问题。而”模型蒸馏“属于模型压缩的一种方法。
1.2 模型误解
上面容器和水的比喻非常经典和贴切,但是会引起一个误解: 人们在直觉上会觉得,要保留相近的知识量,必须保留相近规模的模型。也就是说,一个模型的参数量基本决定了其所能捕获到的数据内蕴含的“知识”的量。
这样的想法是基本正确的,但是需要注意的是:
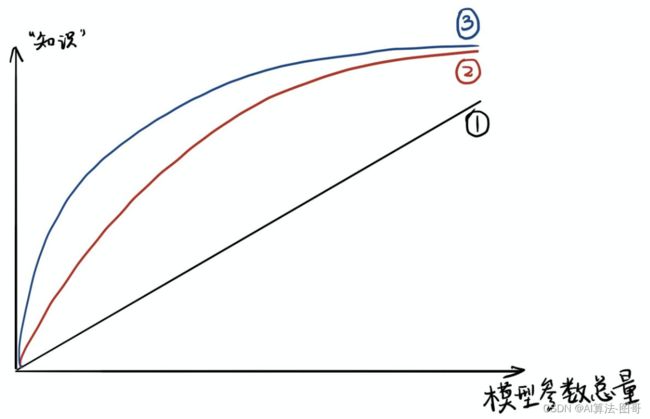
- 模型的参数量和其所能捕获的“知识“量之间并非稳定的线性关系(下图中的1),而是接近边际收益逐渐减少的一种增长曲线(下图中的2和3)
- 完全相同的模型架构和模型参数量,使用完全相同的训练数据,能捕获的“知识”量并不一定完全相同,另一个关键因素是训练的方法。合适的训练方法可以使得在模型参数总量比较小时,尽可能地获取到更多的“知识”(下图中的3与2曲线的对比).
2. 知识蒸馏的理论依据
2.1. Teacher Model和Student Model
知识蒸馏使用的是Teacher—Student模型,其中teacher是“知识”的输出者,student是“知识”的接受者。知识蒸馏的过程分为2个阶段:
- 原始模型训练: 训练"Teacher模型", 简称为Net-T,它的特点是模型相对复杂,也可以由多个分别训练的模型集成而成。我们对"Teacher模型"不作任何关于模型架构、参数量、是否集成方面的限制,唯一的要求就是,对于输入X,
其都能输出Y,其中Y经过softmax的映射,输出值对应相应类别的概率值。 - 精简模型训练: 训练"Student模型", 简称为Net-S,它是参数量较小、模型结构相对简单的单模型。同样的,对于输入X,其都能输出Y,Y经过softmax映射后同样能输出对应相应类别的概率值。
在本论文中,作者将问题限定在分类问题下,或者其他本质上属于分类问题的问题,该类问题的共同点是模型最后会有一个softmax层,其输出值对应了相应类别的概率值。
需要注意的是,这里蒸馏的目的是小网络的概率分布趋近于大网络,而非单纯的正确率趋近于大网络。 Hinton注意到,虽然我们最终分类依靠的是softmax后的最大概率结果,但其实那些概率很小类之间的差别蕴含着网络进行特征提取的很多信息。例如,猫、狗、狮子三个类的输出分别是0.99,0.001,0.009,则很明显:狮子与猫的相似程度比狮子与狗高。
因此,从理论上来说:只有小网络的所有大小输出与大网络都非常相近,才可以视为大小网络间概率分布非常接近。
3. 目标蒸馏-Logits方法
目标蒸馏方法中最经典的论文就是来自于2015年Hinton发表的一篇神作《Distilling the Knowledge in a Neural Network》。下面我们以这篇神作为例,给大家讲讲目标蒸馏方法的原理。
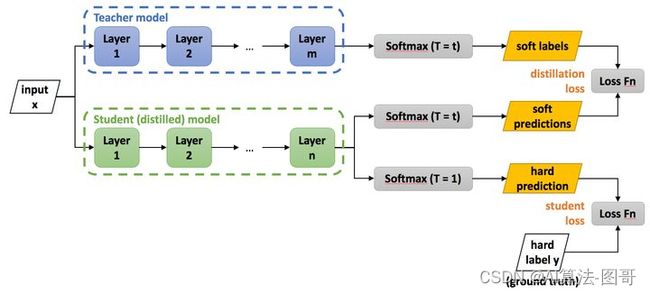
在这篇论文中,Hinton将问题限定在分类问题下,分类问题的共同点是模型最后会有一个softmax层,其输出值对应了相应类别的概率值。在知识蒸馏时,由于我们已经有了一个泛化能力较强的Teacher模型,我们在利用Teacher模型来蒸馏训练Student模型时,可以直接让Student模型去学习Teacher模型的泛化能力。一个很直白且高效的迁移泛化能力的方法就是:使用softmax层输出的类别的概率来作为“Soft-target” 。
3.1 Hard-target 和 Soft-target
传统的神经网络训练方法是定义一个损失函数,目标是使预测值尽可能接近于真实值(Hard- target),损失函数就是使神经网络的损失值和尽可能小。这种训练过程是对ground truth求极大似然。在知识蒸馏中,是使用大模型的类别概率作为Soft-target的训练过程。
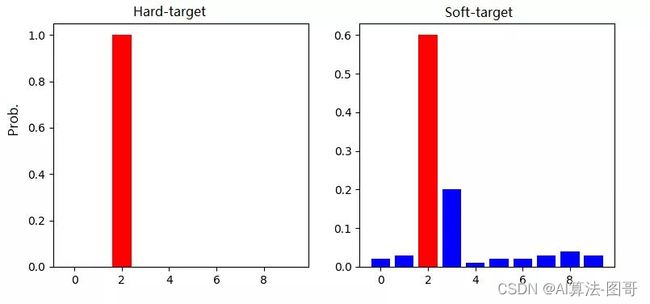
- Hard-target:原始数据集标注的 one-shot 标签,除了正标签为 1,其他负标签都是 0。
- Soft-target:Teacher模型softmax层输出的类别概率,每个类别都分配了概率,正标签的概率最高。
softmax层的输出,除了正例之外,负标签也带有大量的信息,比如某些负标签对应的概率远远大于其他负标签。而在传统的训练过程(hard target)中,所有负标签都被统一对待。也就是说,KD的训练方式使得每个样本给Net-S带来的信息量大于传统的训练方式。
【举个例子】
在手写体数字识别任务MNIST中,输出类别有10个。

假设某个输入的“2”更加形似"3",softmax的输出值中"3"对应的概率为0.1,而其他负标签对应的值都很小,而另一个"2"更加形似"7","7"对应的概率为0.1。这两个"2"对应的hard target的值是相同的,但是它们的soft target却是不同的,由此我们可见soft target蕴含着比hard target多的信息。并且soft target分布的熵相对高时,其soft target蕴含的知识就更丰富。

这就解释了为什么通过蒸馏的方法训练出的Net-S相比使用完全相同的模型结构和训练数据只使用hard target的训练方法得到的模型,拥有更好的泛化能力。
3.2 温度
3.2.1 温度的作用
在我们正常的训练过程中,我们只会关注概率最高结果与正确结果的差别。这种相似性完全是通过足够数量的样本构建的。
因此Hinton的想法是:如何充分利用大网络中的这种结果?如果只是构建所有类的传统损失函数的话,小概率结果对损失函数的贡献微乎其微。解决的方法无非是:在计算损失函数时放大其他类的概率值所对应的损失值。
Hinton用一个简单的方法解决了这一问题:加入温度系数T。改进后的softmax如下。
![]()
我们可以用一个简单的例子看改进后的softmax的效果。
假设某个识别结果中猫、狗、狮子的节点中的值分别为0.9,0.1,0.01。
则他们对应的softmax分类概率分别为:
![]()
计算可得是0.538,0.241,0.221
而添加了T=20以后,
![]()
计算可得是0.3428,0.3293,0.3279
也即,这种方式使得不同类的输出结果被同等的考量了。Hinton用于训练小网络的损失函数,正是T=1的结果与真值的对比,和T=20时大小网络输出所构成的损失两部分组成。实验结果也证实,这种方法促进了小网络的训练效果。
T越高,softmax的output probability distribution越趋于平滑,负标签携带的信息会被相对地放大,模型训练将更加关注负标签。
3.2.2 温度代表了什么,如何选取合适的温度?
温度的高低改变的是Net-S训练过程中对负标签的关注程度: 温度较低时,对负标签的关注,尤其是那些显著低于平均值的负标签的关注较少;而温度较高时,负标签相关的值会相对增大,Net-S会相对多地关注到负标签。
实际上,负标签中包含一定的信息,尤其是那些值显著高于平均值的负标签。但由于Net-T的训练过程决定了负标签部分比较noisy,并且负标签的值越低,其信息就越不可靠。因此温度的选取比较empirical,本质上就是在下面两件事之中取舍:
从有部分信息量的负标签中学习 --> 温度要高一些
防止受负标签中噪声的影响 -->温度要低一些
总的来说,T的选择和Net-S的大小有关,Net-S参数量比较小的时候,相对比较低的温度就可以了(因为参数量小的模型不能capture all knowledge,所以可以适当忽略掉一些负标签的信息)
4. 特征蒸馏
另外一种知识蒸馏思路是特征蒸馏方法,如下图所示。它不像Logits方法那样,Student只学习Teacher的Logits这种结果知识,而是学习Teacher网络结构中的中间层特征。最早采用这种模式的工作来自于论文《FITNETS:Hints for Thin Deep Nets》,它强迫Student某些中间层的网络响应,要去逼近Teacher对应的中间层的网络响应。这种情况下,Teacher中间特征层的响应,就是传递给Student的知识。在此之后,出了各种新方法,但是大致思路还是这个思路,本质是Teacher将特征级知识迁移给Student。因此,接下来我们以这篇论文为主,详细介绍特征蒸馏方法的原理。

4.1 主要解决的问题
这篇论文首先提出一个案例,既宽又深的模型通常需要大量的乘法运算,从而导致对内存和计算的高需求。因此,即使网络在准确性方面是性能最高的模型,其在现实世界中的应用也受到限制。
为了解决这类问题,我们需要通过模型压缩(也称为知识蒸馏)将知识从复杂的模型转移到参数较少的简单模型。
到目前为止,知识蒸馏技术已经考虑了Student网络与Teacher网络有相同或更小的参数。这里有一个洞察点是,深度是特征学习的基本层面,到目前为止尚未考虑到Student网络的深度。一个具有比Teacher网络更多的层但每层具有较少神经元数量的Student网络称为“thin deep network”。
因此,该篇论文主要针对Hinton提出的知识蒸馏法进行扩展,允许Student网络可以比Teacher网络更深更窄,使用teacher网络的输出和中间层的特征作为提示,改进训练过程和student网络的性能。
4.2 模型结构
Student网络不仅仅拟合Teacher网络的Soft-target,而且拟合隐藏层的输出(Teacher网络抽取的特征);
- 第一阶段让Student网络去学习Teacher网络的隐藏层输出(特征蒸馏);
- 第二阶段使用Soft-target来训练Student网络(目标蒸馏)。
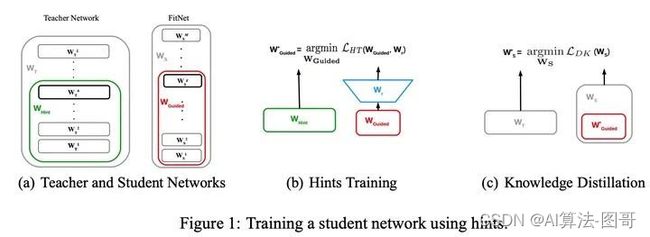
把“宽”且“深”的网络蒸馏成“瘦”且“更深”的网络,需要进行两阶段的训练:
- 第一阶段:首先选择待蒸馏的中间层(即Teacher的Hint layer和Student的Guided layer),如图中绿框和红框所示。由于两者的输出尺寸可能不同,因此,在Guided layer后另外接一层卷积层,使得输出尺寸与Teacher的Hint layer匹配。接着通过知识蒸馏的方式训练Student网络的Guided layer,使得Student网络的中间层学习到Teacher的Hint layer的输出.
- 第二阶段: 在训练好Guided layer之后,将当前的参数作为网络的初始参数,利用知识蒸馏的方式训练Student网络的所有层参数,使Student学习Teacher的输出。由于Teacher对于简单任务的预测非常准确,在分类任务中近乎one-hot输出,因此为了弱化预测输出,使所含信息更加丰富,作者使用Hinton等人论文《Distilling knowledge in a neural network》中提出的softmax改造方法,即在softmax前引入 缩放因子,将Teacher和Student的pre-softmax输出均除以 。也就是上面我们讲的加了温度的softmax。
5. 最后
![]()