Leetcode刷题06-位运算

位运算

基础知识

原码、反码和补码

二进制有三种不同的表示形式：原码、反码和补码，计算机内部使用补码来表示

原码：就是其二进制表示，（其中第一位为符号位）

反码：正数的反码就是原码，负数的反码是符号位不变，其余位取反。

补码：正数的补码就是原码，负数的补码是反码+1

符号位：最高位为符号位，0表示正数，1表示负数，在位运算中符号位也参与位运算

位运算操作

1.按位非操作

整数的二进制每一位都取反（0变成1，1变成0）

00 00 01 01 -> 5
~
11 11 10 10 -> -6  (反码是11 11 10 01， 原码是10 00 01 10，因此是-6) 

2.按位与操作

只有二进制中两个对应位是1才为1

00 00 01 01 -> 5
&
00 00 01 10 -> 6
---
00 00 01 00 -> 4

3.按位或操作

二进制中有一个对应位是1就为1，全为0结果才为0

00 00 01 01 -> 5
|
00 00 01 10 -> 6
---
00 00 01 11 -> 7

4.按位异或操作

只有对应位不同结果为1，否则为0

00 00 01 01 -> 5
^
00 00 01 10 -> 6
---
00 00 00 11 -> 3

异或的操作满足交换律和结合律，即：

A^B = B^A

A^BC = A^(BC)

A^A = 0

A^0 = A

A^BA = A^AB = 0^B = B

5.按位左移操作

num << i将num的二进制表示向左移动i位，右边补0得到的值，左移1位表示十进制的数值加倍。

00 00 10 11 -> 11
11 << 3
01 01 10 00 -> 88

6.按位右移操作

num >> i将num的二进制表示向右移动i位得到的值

00 00 10 11 -> 11
11 >> 3
00 00 00 10 -> 2

题目解析

只出现一次的数字

1.题目描述

题目链接

2.解析思路及代码

对每个数进行异或即可得到答案，因为任何数异或自己等于0，题目中说了只有一个数出现一次，其他都出现两次，因此出现两次的数字异或结果都为0，0异或只出现一次的数等于只出现一次的数，时间复杂度为O(n)

	public int singleNumber(int[] nums) {
        int res = 0;
        for (int i = 0; i < nums.length; i ++ ) {
            res = res ^ nums[i];
        }
        return res;
    }

class Solution:
    def singleNumber(self, nums: List[int]) -> int:
        res = 0
        for item in nums:
            res = res ^ item
        return res

只出现一次的数字 III

1.题目描述

题目链接

2.解题思路及代码

思路：

• 使用哈希表存储每个数字出现的次数，然后将出现次数为1的结果返回
• 使用异或操作和与操作，假设出现一次的数字为x1、x2，首先将所有数异或，根据上一题可得最后的结果为$x=x1\oplus x2$，然后取x的最后一个1，即使用x & -x，因为该位的结果为1，因此可以得出x1和x2的该位一定是不相同的，使用与运算可以将原数组所有数的该位分成两组，x1和x2一定不在同一组，那么每组都只会有一个出现一次的数，即可得到最后的结果。

	public int[] singleNumber(int[] nums) {
        if (nums.length < 2)    return new int[2];
        
        int res = 0;
        for (int num : nums) {
            res ^= num;
        }
        res = res & (-res);
        int num1 = 0, num2 = 0;
        for (int num : nums) {
            if ((res & num) == 0) {
                num1 ^= num;
            } else {
                num2 ^= num;
            }
        }
        return new int[]{num1, num2};
    }

class Solution:
    def singleNumber(self, nums: List[int]) -> List[int]:
        if len(nums) < 2:
            return []
        res = 0
        for num in nums:
            res ^= num
        res = res & (-res)
        num1, num2 = 0, 0
        for num in nums:
            if res & num == 0:
                num1 ^= num
            else:
                num2 ^= num
        return [num1, num2]

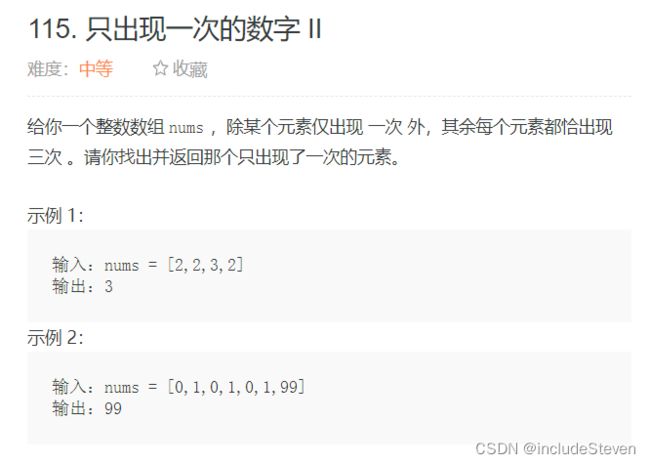
只出现一次的数字 II

1.题目描述

题目链接

2.解题思路及代码

• 使用哈希表映射每个数字的出现次数，然后找出只出现一次的元素
• 获取答案的每一位上的数字，因为其他数都出现三次，因此答案的每一位数字等于所有数字出现的结果和模3，注意如果目标语言不区分有符号数和无符号数，最高位需要特判。

	public int singleNumber(int[] nums) {
        int res = 0;
        for (int i = 0; i < 32; i ++ ) {
            int total = 0;
            for (int num : nums) {
                total += ((num >> i) & 1);
            }
            
            if ((total % 3) == 1) {
                res |= (1 << i);
            }
        }
        return res;
    }

class Solution:
    def singleNumber(self, nums: List[int]) -> int:
        res = 0
        for i in range(32):
            total = sum((num >> i) & 1 for num in nums)
            if total % 3:
                if i == 31:
                    res -= (1 << i)
                else:
                    res |= (1 << i)
        return res

2 的幂

1.题目描述

题目链接

2.解题思路及代码

• 使用n & (n - 1)可以移除n的最低位，判断该结果是否为0即可
• 使用n & (-n)可以取出n的最后一个1，判断该结果是否与n相等即可

	public boolean isPowerOfTwo(int n) {
        return n > 0 && ((n & (n - 1)) == 0);
    }

class Solution:
    def isPowerOfTwo(self, n: int) -> bool:
        return n > 0 and (n == (n & (-n)))

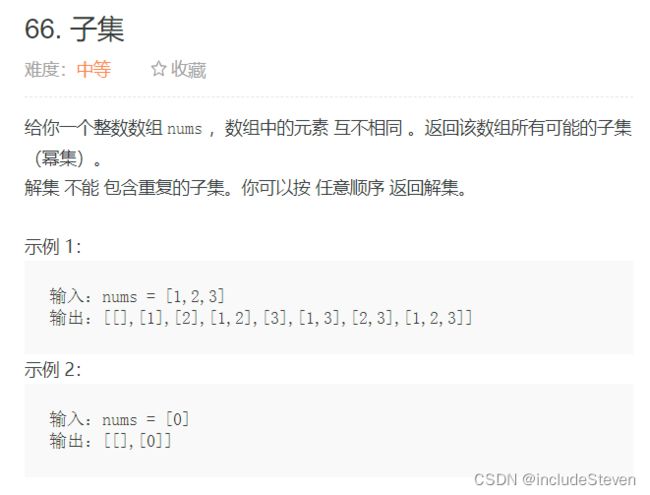
子集

1.题目描述

题目链接

2.解题思路及代码

• 迭代得到结果，数组中出现的每一个结果都可以用二进制对应的位数表示，假设数组有3个元素，那么100表示第一个元素出现，第二个元素不出现，第三个元素不出现，最终的二进制最大值为111。
• 递归求解，对于数组的每一个位置的值，可以选择包含或不包含

	public List<List<Integer>> subsets(int[] nums) {
        List<Integer> tmp = new ArrayList<>();
        List<List<Integer>> ans = new ArrayList<>();
        for (int i = 0; i < (1 << nums.length); i ++ ) {
            tmp.clear();
            for (int j = 0; j < nums.length; j ++ ) {
                if ((i & (1 << j)) != 0) {
                    tmp.add(nums[j]);
                }
            }
            // 注意这里必须重新初始化一个List，否则ans的最后结果都会指向同一个值
            ans.add(new ArrayList<Integer>(tmp));
        }
        return ans;
    }




class Solution {
    List<Integer> tmp = new ArrayList<>();
    List<List<Integer>> ans = new ArrayList<>();
    
    
    public List<List<Integer>> subsets(int[] nums) {
        dfs(0, nums);
        return ans;
    }
    
    public void dfs(int cur, int[] nums) {
        if (cur == nums.length) {
            ans.add(new ArrayList<>(tmp));
            return ;
        }
        
        // 不选择该位
        dfs(cur + 1, nums);
        
        // 选择该位
        tmp.add(nums[cur]);
        dfs(cur + 1, nums);
        tmp.remove(tmp.size() - 1);
    }
}

class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        res = [[]]
        for i in nums:
            # 在每一个现有的结果前加上当前数字
            res = res + [[i] + num for num in res]
        return res