[2022-09-05]神经网络与深度学习第0章-basic‘s basic(part 2)
contents
- basic's basic(part 2)
-
- 写在开头
- PyTorch介绍
- 引用
- 一些概念
-
- 张量
- 算子
- 张量的操作
-
- 创建张量
-
- 指定数据创建张量
- 指定形状创建
- 指定区间创建
- 张量的属性
-
- 张量的形状
- 形状的改变
- 张量的数据类型
- 张量的设备位置
- 张量与numpy数组转换
- 张量的访问
-
- 索引和切片
- 访问张量
- 修改张量
- 张量的运算
-
- 数学运算
- 逻辑运算
- 矩阵运算
-
- 点积运算(torch.dot)
- 矩阵和向量相乘(torch.mv)
- 二维矩阵乘法(torch.mm)
- L2范数(torch.norm)
- 广播机制
- 数据预处理
-
- 读取数据
- 数据切分
- 处理缺失值
- 转换为张量格式
- 写在最后
basic’s basic(part 2)
写在开头
前面我们已经初步了解了numpy、matplotlib等,这些都更加偏向于科学计算和大数据的范畴。本次我们将对PyTorch这一深度学习中非常著名的框架进行初步了解。
PyTorch介绍
PyTorch是一个开源的Python机器学习库,基于Torch,用于自然语言处理等应用程序。——来源:百度百科
引用
注意:PyTorch的库名叫做torch。
import torch
一些概念
张量
张量(tensor)理论是数学的一个分支学科,在力学中有重要应用。张量这一术语起源于力学,它最初是用来表示弹性介质中各点应力状态的,后来张量理论发展成为力学和物理学的一个有力的数学工具。张量之所以重要,在于它可以满足一切物理定律必须与坐标系的选择无关的特性。张量概念是矢量概念的推广,矢量是一阶张量。张量是一个可用来表示在一些矢量、标量和其他张量之间的线性关系的多线性函数。——来源:百度百科
在深度学习和神经网络中,张量是数据的一种表现形式,使用推广的矢量概念,可以用于表示各种数据(矢量、标量、其他张量)之间的线性关系。
算子
算子是一个函数空间到函数空间上的映射O:X→X。广义上的算子可以推广到任何空间,如内积空间等。——来源:百度百科
简单来说,算子是对函数进行某一项操作,或者说和函数没有什么区别。(甲说:ReLu函数,乙说:ReLu算子,听起来就牛逼很多)在神经网络与深度学习中,算子最常用在激活函数部分。
张量的操作
torch.Tensor定义为一种包含单一数据类型元素的多维矩阵。
正如每个语言中有不同数据类型,张量也有很多类型,默认的torch.Tensor为torch.FloatTensor,这里不多加赘述。
创建张量
PyTorch的张量可以通过Python的列表或者序列构成。前面所介绍的numpy.ndarray也可以构成张量。PyTorch中也有一些创建方法。
指定数据创建张量
a = [1,2,3] # 使用np.array([1,2,3])同样可行
b = torch.Tensor(a)
print(b)
输出:![]()
指定形状创建
PyTorch中指定形状创建本人理解共有两种方法:一种为带数据的reshape和类似numpy中的zeros,ones等。
a = [1,2,3]
b = torch.Tensor(a)
c1 = torch.reshape(b,(-1,1)) # 使用数据指定形状,将原来的转置
print(c1)
c2 = torch.ones((2,2)) # 创建全1张量:2x2
print(c2)
c3 = torch.zeros((2,2)) # 创建全0张量:2x2
print(c3)
c4 = torch.rand((2,2)) # 创建随机张量:2x2
print(c4)
指定区间创建
指定区间创建的参数和numpy非常非常非常像!使用torch.linspace函数即可。
torch.linspace(start, end, steps=100, out=None, dtype=None, layout=torch.strided, device=None, requires_grad=False)
常用的属性如下:
| 属性 | 默认值 | 解释 |
|---|---|---|
| start | / | 开始值 |
| end | / | 结束值 |
| steps | 100 | 区间等分点数 |
| dtype | None | 返回张量的数据类型 |
a = torch.linspace(0,1145,14)
print(a)
张量的属性
张量的形状
和numpy比较类似,PyTorch中张量的形状也使用shape属性,具体如下例:
a = torch.Tensor([[1,1,4],[5,1,4],[191,98,10]])
print(a.shape)
输出:![]()
形状的改变
这边和前面所提“指定形状创建”内容相似,需要注意的是形状改变前后总元素的数量不能变化。
a = torch.Tensor([[1,1,4],[5,1,4],[191,98,10]])
print(a.reshape(1,9))
输出:![]()
张量的数据类型
这部分和numpy也是非常非常相似的,使用type函数即可。代码如下:
a = torch.Tensor([[1,1,4],[5,1,4],[191,98,10]])
a.type()
输出:![]()
张量的设备位置
众所周知,深度学习可以通过CPU和GPU进行计算,这时候我们就需要知道这个计算在什么地方运行,针对不同的数据运算进行处理的优化。这里使用Tensor的device属性即可。本实验在CPU设备上进行。
a = torch.Tensor([[1,1,4],[5,1,4],[191,98,10]])
print(a.device)
#print(a.device.type)也可
输出:![]()
张量与numpy数组转换
numpy转换成张量前面已经介绍过,代码如下:
a = np.array([[1,1,4],[5,1,4],[191,98,10]])
b = torch.Tensor(a)
print(b)
- 不是训练中的张量
a = torch.Tensor([[1,1,4],[5,1,4],[191,98,10]])
b = a.numpy()
print(b)
- 训练中的张量转换,首先需要使用detach取消参数追踪
a = torch.Tensor([[1,1,4],[5,1,4],[191,98,10]]) # 这里假设a是训练中的参数
b = a.detach().numpy() # 现实情况中,如果对训练中的张量不用detach转换,会报错
print(b)
张量的访问
索引和切片
- 索引使用torch.argwhere函数来查找元素,返回值也是Tensor类型。
print(torch.argwhere(a==1))
print(torch.argwhere(a<514))
print(torch.argwhere(a!=114))
- 张量的切片与numpy别无二异,具体操作类别因为与numpy相同,不再进行赘述。下面给出样例代码:
a = torch.Tensor([[1,1,4],[5,1,4],[191,98,10]])
print(a[1:])
print(a[:,1:2])
访问张量
访问张量方式和numpy相同,不再赘述,代码如下:
a = torch.Tensor([[1,1,4],[5,1,4],[191,98,10]])
print(a[1])
print(a[1,2])
print(a[[1,2],[0,1]])
修改张量
- 修改张量的值如下:
a = torch.Tensor([[1,1,4],[5,1,4],[191,98,10]])
a[0] = -1
a[1] = torch.Tensor([-5,-1,-4])
a[2] = a[2] * (-1)
print(a)
- 在更多情况下,我们需要修改张量的数据类型,在这种情况下,PyTorch为我们直接封装好了转换的函数和是否可以转化的判断函数。代码如下:
print(torch.can_cast(torch.double, torch.float))
a = torch.Tensor([[1,1,4],[5,1,4],[191,98,10]])
b = a.int()
c = a.double()
print(a.type)
print(b.type)
print(c.type)
张量的运算
其实张张量的运算也属于张量的修改范畴,然而其中有非常多的计算操作,因此单独进行介绍。
数学运算
- 四则运算
a = torch.Tensor([[1,1,4],[5,1,4],[191,98,10]])
print(a)
a = a * -1
print(a)
a = a - 1
print(a)
a += 1
print(a)
a /= 6
print(a)
- 一些数学函数计算,有很多函数,具体可打开PyTorch官网查看官方文档。
a = torch.Tensor([[-1,-1,-4],[-5,-1,-4],[-191,-98,-10]])
a = torch.abs(a) # 绝对值
print(a)
a = torch.sqrt(a) # 求平方根
逻辑运算
在深度学习与神经网络中有许多逻辑和结构化的计算,这些计算需要用到逻辑运算,PyTorch的张量也支持逻辑的运算。需要注意的是,逻辑运算仅在PyTorch1.2以后的版本中支持,通过BoolTensor进行逻辑运算。
逻辑运算的操作和正常的各种编程语言中的符号定义相同。其他张量转化为布尔张量使用bool函数,其中0为False,非0为True的定义与其他主流语言相同。具体代码如下:
a = torch.Tensor([0,1,1,0,6]).bool()
b = torch.Tensor([0,1,0,1,0]).bool()
print(a)
print(b)
print(a & b) # 与运算
print(a | b) # 或运算
print(~a) # 取反
print(a ^ b) # 异或运算
输出:![[2022-09-05]神经网络与深度学习第0章-basic‘s basic(part 2)_第5张图片](http://img.e-com-net.com/image/info8/15a2c413f6324be3a705bcaaa6c6c1bf.jpg)
比较运算等也属于逻辑运算的范畴,下面的代码给出几种比较和逻辑判断:
a = torch.Tensor([0,1,1,0,6]).bool()
b = torch.Tensor([0,1,0,1,0]).bool()
print(torch.eq(a,b)) # 每个分量进行判断是否相等
print(torch.equal(a,b)) # 整体进行判断是否相等
print(torch.any(a)) # 判断是否存在True
print(torch.all(a)) # 判断是否全为True
矩阵运算
矩阵运算可以说是神经网络与深度学习中使用最多的计算方式了。线性代数的发展给予很多问题矩阵形式的解决方法。PyTorch张量支持矩阵的运算。
- 矩阵与常量运算:与之前的数学运算中介绍相同,不再赘述
- 矩阵与矩阵的简单数学运算:两个矩阵进行简单的四则运算或者逻辑运算,其方法和前面介绍的方法相同,只是需要注意两个参与运算的张量形状需要相同,否则无法进行运算
- 矩阵的特有运算:
点积运算(torch.dot)
与numpy中dot能够计算矩阵乘法不同,PyTorch中的dot函数仅支持一维张量进行运算,即计算内积。
定义 a = < v 1 , v 2 , ⋯ , v n > , b = < w 1 , w 2 , ⋯ , v n > \bf{a}=
则内积c为:
c = ∑ i = 1 n v i w i c=\sum_{i=1}^{n}v_iw_i c=i=1∑nviwi
具体代码如下:
a = torch.Tensor([1,1,4,5,1,4])
b = torch.Tensor([1,9,1,9,8,1])
print(torch.dot(a,b))
输出:![]()
矩阵和向量相乘(torch.mv)
矩阵和向量相乘是前一种情况的扩展情况,将矩阵中每行进行前一种情况的内积计算,最终得到每行的内积结果。
a = torch.Tensor([ [1,1,4],
[5,1,4]])
b = torch.Tensor([1,9,1])
print(torch.mv(a,b))
输出:![]()
二维矩阵乘法(torch.mm)
矩阵运算定义如下:给定两个矩阵,分别为mxn和nxp,
a = [ a 11 ⋯ a 1 n ⋮ ⋯ ⋮ a m 1 ⋯ a m n ] , b = [ b 11 ⋯ b 1 p ⋮ ⋯ ⋮ b n 1 ⋯ b n p ] a = \begin{bmatrix} a_{11} & \cdots & a_{1n} \\ \vdots & \cdots & \vdots \\ a_{m1} & \cdots & a_{mn} \end{bmatrix}, b = \begin{bmatrix} b_{11} & \cdots & b_{1p} \\ \vdots & \cdots & \vdots \\ b_{n1} & \cdots & b_{np} \end{bmatrix} a=⎣ ⎡a11⋮am1⋯⋯⋯a1n⋮amn⎦ ⎤,b=⎣ ⎡b11⋮bn1⋯⋯⋯b1p⋮bnp⎦ ⎤
则得到点乘后的矩阵c,大小为mxp,其中第i行第j列元素值为:
c i j = ∑ k = 1 n a i k b k j c_{ij} = \sum_{k=1}^{n}a_{ik}b_{kj} cij=k=1∑naikbkj
另外,还有高维矩阵乘法torch.matmul。
a = torch.Tensor([ [1,1,4],
[5,1,4]])
b = torch.Tensor([ [1,9,1],
[9,8,1],
[0,0,0]])
print(torch.mm(a,b))
L2范数(torch.norm)
L2范数计算张量的模。定义: a = [ a 11 ⋯ a 1 n ⋮ ⋯ ⋮ a m 1 ⋯ a m n ] a = \begin{bmatrix} a_{11} & \cdots & a_{1n} \\ \vdots & \cdots & \vdots \\ a_{m1} & \cdots & a_{mn} \end{bmatrix} a=⎣ ⎡a11⋮am1⋯⋯⋯a1n⋮amn⎦ ⎤
则其模为:
∣ ∣ a ∣ ∣ = ∑ i = 1 m ∑ j = 1 n a i j 2 ||a|| = \sqrt[]{\sum_{i=1}^{m}\sum_{j=1}^{n}a_{ij}^2} ∣∣a∣∣=i=1∑mj=1∑naij2
a = torch.Tensor([ [1,1,4],
[5,1,4]])
print(torch.norm(a))
输出:![]()
广播机制
张量的广播机制旨在处理两个张量维度不同或不匹配时的计算问题。这个部分本人接触较少,具体可以参考PyTorch官方文档进一步了解,这里仅介绍一些初步使用方法。
注意!当一对张量满足下面的条件时,它们才是可以被“广播”的。
- 每个张量至少有一个维度。
- 迭代维度尺寸时,从尾部(也就是从后往前)开始,依次每个维度的尺寸必须满足以下之一:
- 相等。
- 其中一个张量的维度尺寸为1。
- 其中一个张量不存在这个维度。
a = torch.Tensor([5,1,4])
b = torch.Tensor([ [1,9,1],
[9,8,1],
[0,0,0]])
print(a.shape)
print(b.shape)
print(a+b) # 这边就发生了广播
a = torch.Tensor([[[5,1,4]]])
b = torch.Tensor([ [1,9,1],
[9,8,1],
[0,0,0]])
print(a.shape)
print(b.shape)
print(a+b)
数据预处理
数据预处理在非结构化或者内容残缺的结构化的数据操作中非常常见,例如Kaggle入门比赛之一的Titanic数据集中便有很多值无法直接使用而需要进行预处理。
数据预处理最常使用的库为pandas,功能非常强大。
读取数据
pandas支持读取txt、csv、excel等多种多样形式的数据文件和python代码中其他的数据。其库引用如下:
import pandas as pd
pandas读取数据的函数比较相似,为pd.read_xxx(这里的xxx可以是csv、clipboard、excel、…)
- 读取数据集 house_tiny.csv、boston_house_prices.csv、Iris.csv
这里读取的房子、波士顿房价、鸢尾花数据集均为csv格式
df_house_tiny = pd.read_csv('./house_tiny.csv')
df_boston_house_prices = pd.read_csv('./boston_house_prices.csv')
df_iris = pd.read_csv('./Iris.csv')
在读取完后,我们可以使用head(i)函数查看前i行的数据。读取后类型为DataFrame,这是pandas所定义的数据表的类。这里给出house_tiny的例子:
df_house_tiny.head(2) # 列出前两行
数据切分
pandas的数据切分功能非常多,可以根据列名、指定行等等进行数据切分,下面代码给出两种最常用的切分:
print(df_house_tiny['Alley']) # 按照列名切分
print(df_house_tiny.iloc[1:,0]) # 按照[行,列]进行切分
处理缺失值
pandas对缺失值有两种处理方式:丢弃(dropna)和填充(fillna)。
df_house_tiny = df_house_tiny.fillna(
df_house_tiny.iloc[:,0:2].mean())
print(df_house_tiny)
输出:![[2022-09-05]神经网络与深度学习第0章-basic‘s basic(part 2)_第10张图片](http://img.e-com-net.com/image/info8/0613878a057f47cb82c609e794af4d6d.jpg)
再看Alley列,其由字符串构成,而缺失值数量过多,于是我们不妨设置两个列:一个列表示Alley为Pave,另一列表示为Alley为NaN。此时我们需要使用get_dummies函数。
df_house_tiny = pd.get_dummies(df_house_tiny,dummy_na=True).iloc[:,[0,2,3,1]] # 将价格移动到最后一列
print(df_house_tiny)
转换为张量格式
转换成PyTorch中的张量,需要先将DataFrame中的数据读出(使用.values属性)或者转成numpy格式(使用.to_numpy函数)。代码如下:
ret = torch.Tensor(df_house_tiny.values)
# ret = torch.Tensor(df_house_tiny.to_numpy())也可
print(ret)
输出:![[2022-09-05]神经网络与深度学习第0章-basic‘s basic(part 2)_第12张图片](http://img.e-com-net.com/image/info8/59a88e32ed1d4ce29c6a1bccb71412c3.jpg)
对给出的三个数据文件进行如此处理,均能够得到需要的数据。
注意,对于iris中非数值类型的花种类数据列,我们可以使用one-hot编码,也可以使用get_dummies来得到多个表示种类的列。本文使用get_dummies进行处理,最终得到波士顿房价和鸢尾花张量如下:
![[2022-09-05]神经网络与深度学习第0章-basic‘s basic(part 2)_第13张图片](http://img.e-com-net.com/image/info8/f0898e76a6a5483294f4051118b20bf3.jpg)
写在最后
本章节我们了解到了神经网络与深度学习中非常重要的张量的使用方法以及其他的一些概念。在PyTorch中,我们熟悉了PyTorch中张量类型的简单使用方法,知道的张量的属性、操作和转换。在数据处理中,我们了解到了数据的读取、预处理和转换的初步内容。PyTorch中还有很多内容如卷积、激活函数、损失函数等内容等待学习,pandas中同样也有很多数据统计的内容值得去探索。本人还是比较建议去这些库的官网阅读相关英文原文档、或者有能力者更进一步去Github上查看源代码来了解这些库的更多能力和实现方式。
![[2022-09-05]神经网络与深度学习第0章-basic‘s basic(part 2)_第1张图片](http://img.e-com-net.com/image/info8/c0342fa2ef704531947b39790eb92f2d.png)
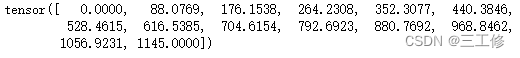

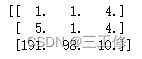

![[2022-09-05]神经网络与深度学习第0章-basic‘s basic(part 2)_第2张图片](http://img.e-com-net.com/image/info8/b4c5882fa77646a0ac23b9652859bfee.png)


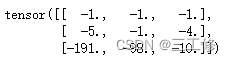

![[2022-09-05]神经网络与深度学习第0章-basic‘s basic(part 2)_第3张图片](http://img.e-com-net.com/image/info8/9b7d7b165168423495f37a3b940a384d.png)
![[2022-09-05]神经网络与深度学习第0章-basic‘s basic(part 2)_第4张图片](http://img.e-com-net.com/image/info8/969b1996481041aca1062a2d1e108c60.png)


![[2022-09-05]神经网络与深度学习第0章-basic‘s basic(part 2)_第6张图片](http://img.e-com-net.com/image/info8/a8239eeaa81c48d9ae55f186a7fd0ec6.jpg)
![[2022-09-05]神经网络与深度学习第0章-basic‘s basic(part 2)_第7张图片](http://img.e-com-net.com/image/info8/a7a5a2c06eb34afc86b5d16a4a5be379.jpg)
![[2022-09-05]神经网络与深度学习第0章-basic‘s basic(part 2)_第8张图片](http://img.e-com-net.com/image/info8/9a3c4155c1a04612b7a90cae9a32846c.jpg)
![[2022-09-05]神经网络与深度学习第0章-basic‘s basic(part 2)_第9张图片](http://img.e-com-net.com/image/info8/cc9fb95047784353bb8ce34d31b258e8.jpg)
![[2022-09-05]神经网络与深度学习第0章-basic‘s basic(part 2)_第11张图片](http://img.e-com-net.com/image/info8/eb95268d74a04038a2d95d6118ad882b.jpg)