【数据结构初阶】栈&&栈的面试题

大家好我是沐曦希

1.栈

1.1 栈的概念及结构

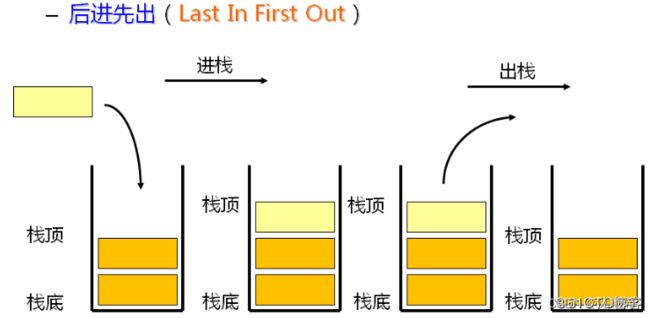
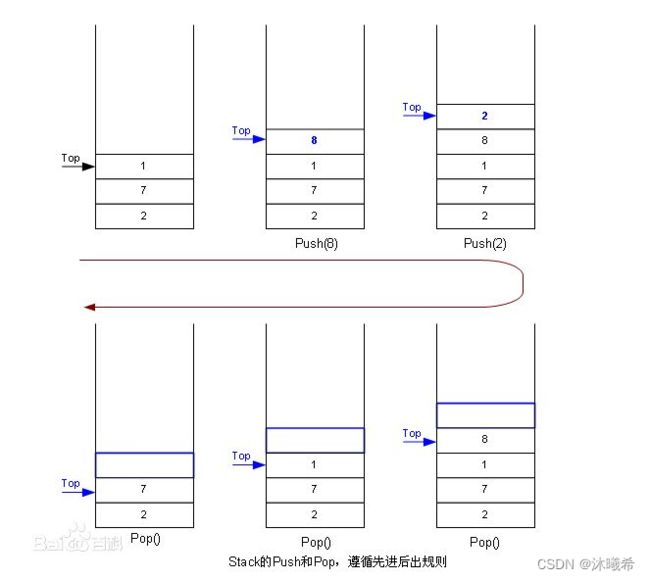
栈：一种特殊的线性表，其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端A称为栈顶，另一端称为栈底。栈中的数据元素遵守后进先出LIFO（Last In First Out）的原则。
压栈：栈的插入操作叫做进栈/压栈/入栈，入数据在栈顶。
出栈：栈的删除操作叫做出栈。出数据也在栈顶。

注意：要与操作系统中的栈进行区分。这是数据结构中的栈，操作系统中的栈是内存区域划分出来的栈，是用来存储函数中局部变量，用于为函数开辟栈帧。

1.2 的实现

栈的实现一般可以使用数组或者链表实现，相对而言数组的结构实现更优一些。因为数组在尾上插入数据的代价比较小。

// 下面是定长的静态栈的结构，实际中一般不实用，所以我们主要实现下面的支持动态增长的栈
typedef int STDataType;
#define N 10
typedef struct Stack
{
	STDataType _a[N];
	int _top; // 栈顶
}Stack;

Stack.h

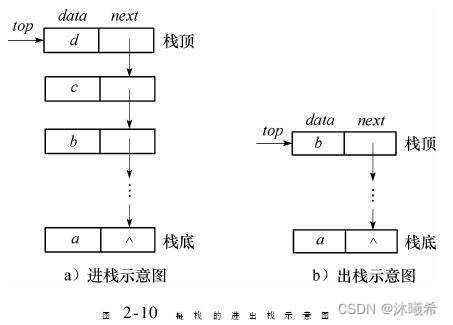
下面采用动态数组来实现栈。
解耦 – 低耦合 高内聚
数据结构建议不要直接访问结构数据，一定要通过函数接口访问。
因为每个栈的实现方法可能不同，有单链表实现的，有带头双向链表实现的，还有顺序表实现的，这些用户是不清楚的，只有实现该栈的程序员知道实现所用的方法，那么就要要分装一个函数来求栈中数据的个数。
还有栈顶top的指向：
第一种情况：top指向最后一个数据的下一个。
第二种情况：top指向最后一个数据。

#pragma once
#define _CRT_SECURE_NO_WARNINGS 1
#include
#include
#include
#include
typedef int STDataType;
typedef struct stack
{
	STDataType* a;
	int top;
	int capacity;
}ST;
// 初始化栈
void StackInit(ST* ps);
//销毁栈
void StackDestory(ST* ps);
// 入栈
void StackPush(ST* ps, STDataType data);
// 出栈
void StackPop(ST* ps);
//检测栈是否为空
bool StackEmpty(ST* ps);
// 获取栈顶元素
STDataType StackTop(ST* ps);
// 获取栈中有效元素个数
int StackSize(ST* ps);

test.c

#include"Stack.h"
void test1()
{
	ST p;
	StackInit(&p);
	StackPush(&p, 1);
	printf("%d\n", StackTop(&p));
	StackPush(&p, 2);
	printf("%d\n", StackTop(&p));
	StackPush(&p, 3);
	printf("%d\n", StackTop(&p));
	StackPush(&p, 4);
	printf("%d\n", StackTop(&p));
	StackPush(&p, 6);
	printf("%d\n", StackTop(&p));
	StackPush(&p, 5);
	printf("%d\n", StackTop(&p));
	int i = 0;
	for (i = 0; i < p.top; i++)
	{
		printf("%d ", p.a[i]);
	}
	printf("\n");
	printf("size:%d\n", StackSize(&p));
	StackPop(&p);
	printf("%d\n", StackTop(&p));
	StackPop(&p);
	printf("%d\n", StackTop(&p));
	StackPop(&p);
	printf("%d\n", StackTop(&p));
	StackPop(&p);
	printf("%d\n", StackTop(&p));
	StackPop(&p);
	printf("%d\n", StackTop(&p));
	for (i = 0; i < p.top; i++)
	{
		printf("%d ", p.a[i]);
	}
	printf("\n");
	printf("size:%d\n", StackSize(&p));
	StackDestory(&p);
}
int main()
{
	test1();
	test2();
	return 0;
}

Stack.c

1.因为传的是地址，所以函数都应该断言一下ps是否为空，否则会对空指针解引用，程序会崩溃。
2.只有一个接口新增数据，所以可以不用分装一个函数来实现扩容。
3.一定要实现销毁栈函数，否则内存泄漏。

#include"Stack.h"
void StackInit(ST* ps)
{
	assert(ps);
	ps->a = NULL;
	ps->top = 0;
	ps->capacity = 0;
}
void StackDestory(ST* ps)
{
	assert(ps);
	free(ps->a);
	ps->capacity = 0;
	ps->top = 0;
	ps->a = NULL;
}
void StackPush(ST* ps, STDataType data)
{
	assert(ps);
	if (ps->capacity == ps->top)
	{
		int newcapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
		STDataType* tmp = (STDataType*)realloc(ps->a, sizeof(STDataType) * newcapacity);
		if (tmp == NULL)
		{
			perror("realloc fail");
			exit(-1);
		}
		ps->capacity = newcapacity;
		ps->a = tmp;
	}
	ps->a[ps->top] = data;
	++ps->top;
}
void StackPop(ST* ps)
{
	assert(ps);
	assert(!StackEmpty(ps));
	//断言栈是否还有数据
	--ps->top;
}
bool StackEmpty(ST* ps)
{
	assert(ps);
	return ps->top == 0;
	//没有数据返回true，有则返回false
}
STDataType StackTop(ST* ps)
{
	assert(ps);
	assert(!StackEmpty(ps));
	//断言栈是否还有数据
	return ps->a[ps->top - 1];
}
int StackSize(ST* ps)
{
	assert(ps);
	return ps->top;
}

3.栈面试题

3.1 有效的括号

题目链接：20. 有效的括号

因为C语言没有队列，所以需要自行写一个队列。
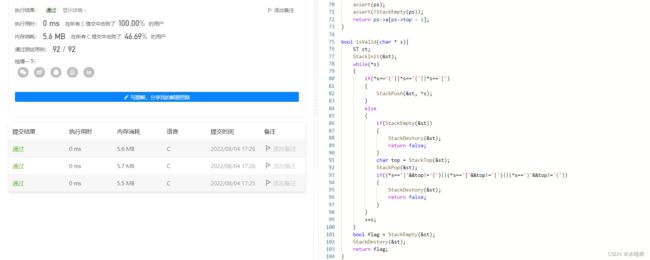
思路可以把左括号入栈，右括号不入栈，与栈的栈顶对应括号进行比对，不是同一类型括号则return false；是同一类型，则将该栈顶对应的括号出栈，并s++一下，则比对下一个。
要注意的是：
1.全是右括号，即没有左括号，需要在比对时候加上

if(StackEmpty(&st))
            {
                StackDestory(&st);
                return false;
            }

判断栈是否为空，为空则结束，不为空进行比对。
2.全是左括号或者有剩的左括号，此时在循环结束之后加上：

bool flag = StackEmpty(&st);

来判断栈是否为空，不为空返回fasle，为空返回true。

代码

#include
#include
#include
#include
typedef char STDataType;
typedef struct stack
{
	STDataType* a;
	int top;
	int capacity;
}ST;
// 初始化栈
void StackInit(ST* ps);
//销毁栈
void StackDestory(ST* ps);
// 入栈
void StackPush(ST* ps, STDataType data);
// 出栈
void StackPop(ST* ps);
//检测栈是否为空
bool StackEmpty(ST* ps);
// 获取栈顶元素
STDataType StackTop(ST* ps);
void StackInit(ST* ps)
{
	assert(ps);
	ps->a = NULL;
	ps->top = 0;
	ps->capacity = 0;
}
void StackDestory(ST* ps)
{
	assert(ps);
	free(ps->a);
	ps->capacity = 0;
	ps->top = 0;
	ps->a = NULL;
}
void StackPush(ST* ps, STDataType data)
{
	assert(ps);
	if (ps->capacity == ps->top)
	{
		int newcapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
		STDataType* tmp = (STDataType*)realloc(ps->a, sizeof(STDataType) * newcapacity);
		if (tmp == NULL)
		{
			perror("realloc fail");
			exit(-1);
		}
		ps->capacity = newcapacity;
		ps->a = tmp;
	}
	ps->a[ps->top] = data;
	++ps->top;
}
void StackPop(ST* ps)
{
	assert(ps);
	assert(!StackEmpty(ps));
	--ps->top;
}
bool StackEmpty(ST* ps)
{
	assert(ps);
	return ps->top == 0;
}
STDataType StackTop(ST* ps)
{
	assert(ps);
	assert(!StackEmpty(ps));
	return ps->a[ps->top - 1];
}

bool isValid(char * s){
    ST st;
    StackInit(&st);
    while(*s)
    {
        if(*s=='('||*s=='{'||*s=='[')
        {
            StackPush(&st, *s);
        }
        else
        {
            //取到右括号；栈为空，说明前面左括号数量不匹配
            if(StackEmpty(&st))
            {
                StackDestory(&st);
                return false;
            }
            char top = StackTop(&st);
            StackPop(&st);
            if((*s=='}'&&top!='{')||(*s==']'&&top!='[')||(*s==')'&&top!='('))
            {
                StackDestory(&st);
                return false;
            }
        }
        ++s;
    }
    //栈不为空，说明数量不匹配
    bool flag = StackEmpty(&st);
    StackDestory(&st);
    return flag;
}

4.概念选择题

选择题

1.一个栈的初始状态为空。现将元素1、2、3、4、5、A、B、C、D、E
依次入栈，然后再依次出栈，则元素出栈的顺序是（ ）。
A 12345ABCDE
B EDCBA54321
C ABCDE12345
D 54321EDCBA
//先进后出，正确出栈顺序：EDCBA54321

答案：B

2.若进栈序列为 1,2,3,4 ，进栈过程中可以出栈，
则下列不可能的一个出栈序列是（）
A 1,4,3,2
B 2,3,4,1
C 3,1,4,2
D 3,4,2,1

进栈过程中可以出栈，先进后出
A 1，4，3，2是可以的。第一次只入栈1并且1跟着出栈；第二次入栈2，3，4，第二出栈顺序4，3，2。
B 2 , 3 , 4 , 1是可以的。第一次入栈1，2，第一次只出栈2；第二次入栈3，第二次只出栈3；第三次入栈4，第三次出栈4，1。
D 3 , 4 , 2 , 1是可以的。第一次入栈3，2，1，第一次只出栈3；第二次入栈4，第二次出栈4，3，1。
C 3 , 1 , 4 , 2是不可以的。第一次入栈3，2，1，第一次出栈顺序应该是3，2，1，而不是3，1，跳过2。

答案：C

5.写在最后

那么栈就到这里结束啦。