NVIDIA CUDA 高度并行处理器编程（四）：CUDA性能优化

kernel 函数的执行速度在不同设备上差异很大，这是因为不同设备的资源约束不同。下面将会讨论资源约束的主要类型，以及它们如何限制 kernel 函数的执行性能。在特定设备上，可通过用一种资源代替另一种资源的方式来提高程序的性能。

1.WARP 和线程执行

（二）中写到，CUDA 设备将若干线程捆绑执行。把每个线程块划分成 warp。warp 的执行由 SIMD 硬件完成。

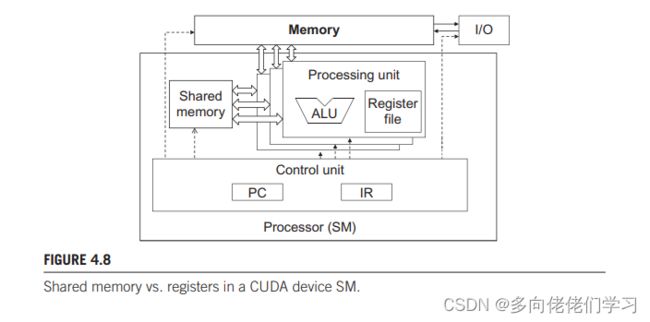
上图说明了 warp 的组织形式。处理器只有一个控制单元进行取指和译码操作，同一个控制信号进入多个处理单元，每个处理单元执行 warp 中的一个线程。由于所有处理单元都由一条指令控制，所以它们执行结果差异就取决于各各单元寄存器中不同的操作数。

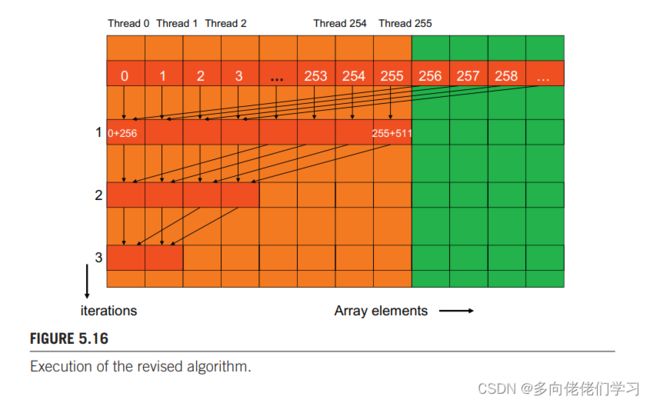
线程块根据线程索引划分为 warp。当前所有 CUDA 设备都是每个 warp 包括 32 个线程，线程块根据索引划分为 warp ，不同维度的线程块划分形式不同：

• 一维：warp n 从线程 32 x n 开始到32（n + 1）- 1 结束，对于线程数不是 32 倍数的线程块，最后一个 warp 将会用别的快中的线程填充至 32 个。例如一个块有 48 个线程， warp 0 从线程 0 - 31，warp 1 从线程 32 - 63，后16个线程是用其他块中的线程来填充的。

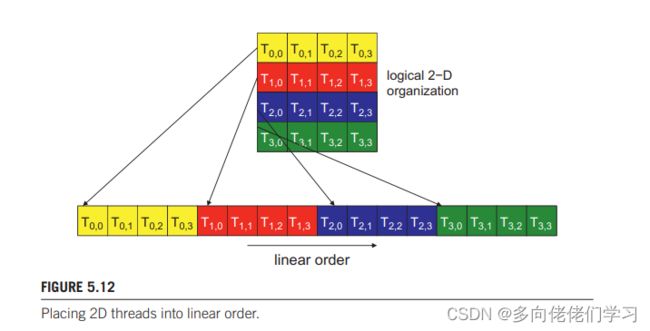
• 二维：在划分 warp 前会把维度映射到一个线性顺序中，可以将二维线程块中每个线程看成成 T_threadIdx.y,_threadIdx.x 的形式。对应的一维形式如下图下部，前四个对应 threadIdx.y = 0 的线程，按 threadIdx.x 递增的顺序排列，第五个到第八个对应 threadIdx.y = 1 的线程，以此类推。在这个例子中，16个线程组织成半个 warp ，会用另外 16 个线程填充这个 warp 。

• 三维：会先将 threadIdx.z = 0，的二维线程块线性排列，再将 threadIdx.z = 0，的二维线程块线性排列，以此类推。
  
  CUDA warp 中的线程可能同时执行相同的指令，此时效率最高，也可能执行不同的指令，此时效率会降低。书上的说法就是，当一个 warp 中的所有线程处理他们的数据时采用相同的控制流路径，它的工作效率最高，例如在一个 if-else 结构中，所有线程都执行 if 部分或 else 部分时。当一个 warp 中的线程分别采用不同的控制流路径时，warp 按顺序执行这些路径，增加执行时间，例如一个 warp 中的线程有些执行 if 语句，有些执行 else 语句时。
  当同一个 warp 中的线程执行控制流中的不同路径时，这些线程在执行过程中就出现了分支（diverge）。分支出现时硬件需要遍历其他路径，确保所有线程能自己做出选择。假定一个 warp 中不同的线程要执行的 for 循环的次数不同，可能会迭代 7， 8次，所有线程都会经历前 7 次迭代，执行第 8 次迭代会使用两条路径，继续迭代的线程通过其中一条路径，不需要继续迭代的线程会经过另一条路径。

求和归约算法（一）：
并行归约（Reduction）是一种很基础的并行算法，简单来说，我们有N个输入数据，使用一个符合结合律的二元操作符作用其上，最终生成1个结果。这个二元操作符可以是求和、取最大、取最小、平方、逻辑与或等等。
由于加法的交换律和结合律，数组可以以任意顺序求和。所以我们会自然而然产生这样的思路：首先把输入数组划分为更小的数据块，之后用一个线程计算一个数据块的部分和，最后把所有部分和再求和得出最终结果。

上面演示了单个线程块内的归约求和过程，结合下面的代码解释：

• 13行第一轮循环，对应上图的第二行，数组中索引为偶数的值被对应部分和替代。
• 第二轮循环，对应上图第三行，数组中索引为 4 的整数倍的值被对应部分和替代。
• 第三轮循环，对应上图第四行，数组中索引为 8 的整数倍的值被对应部分和替代。
• …
• 直至 stride 的值为 blockDim.x 的一半，这一步块内和就计算完了，并存储在threadIdx.x 为 0 的线程中。

但对于不同块内的和，就需要将每个块内 threadIdx.x 为 0 的线程的和相加才能求得总的向量和。

归约求和代码（一）：

#include
#include
#include
#define THREAD_LENGTH 256
__global__ void reduceSum(double *d_A, int n){
    unsigned int t = threadIdx.x;
    __shared__ double partialSum[THREAD_LENGTH];
    if(blockIdx.x*blockDim.x + t < n)
        partialSum[t] = d_A[blockIdx.x*blockDim.x + t];
    else 
        partialSum[t] = 0;
    __syncthreads();  //将数组加载到共享存储器。
    for(unsigned int stride = 1; stride < blockDim.x; stride *= 2){
        if(t % (2*stride) == 0)
            partialSum[t] += partialSum[t + stride];
        __syncthreads();
    }
    /*将每个线程块内 threadIdx.x 为零的线程中的值传回d_A。
    主机函数中将会对这几个线程求和，以得到最终的和。*/
    if(t == 0)   
        d_A[blockIdx.x*blockDim.x + t] = partialSum[t];
}

void test(double *A, int n){
    double *d_A;
    int size = n * sizeof(double);
    cudaMalloc(&d_A, size);
    cudaMemcpy(d_A, A, size, cudaMemcpyHostToDevice);
    reduceSum<<<ceil((double)n/THREAD_LENGTH), THREAD_LENGTH>>>(d_A, n);
    cudaMemcpy(A, d_A, size, cudaMemcpyDeviceToHost);
    cudaFree(d_A);
    double result = 0;
    for(int i = 0;i < ceil((double)n/THREAD_LENGTH);++i){
        result += A[i*THREAD_LENGTH];    //对每个块内部分和求和
    }
    A[0] = result;                       //通过A[0]传回
}

int main(int argc, char **argv){
    int n = atoi(argv[1]);
    double *A = (double *)malloc(n * sizeof(double));
    for(int i = 0; i < n;++i){
        A[i] = 1.0;
    }
    test(A, n);
    printf("%lf\n", A[0]);
    free(A);
    return 0;
}

测试结果如下：

算法分析：
第一轮需要进行 N/2 次加法操作，第二轮需要 N/4 次加法操作，最后一轮只需进行 1 次加饭操作。总共有 log₂（N）轮计算。kernel 函数完成的加法操作总数为 N/2 + N/4 + N/8 + … + 1 = N-1。因此归约算法的计算复杂度为 O(N)。很明显时间复杂度为 O(log₂N)。
上面的 kernel 函数中明显有分支。同一个 warp 在全程循环中都有两个控制流路径，即一部分满足 if 条件参与运算，另一部分不满足 if 条件不参与运算。

求和归约算法（二）：

继续结合下面的代码解释。

• 第一轮循环中不在采用相邻元素相加，两个相加元素中间的距离是每一部分大小的一半。把 stride 初始化为线程块大小的一半，能实现上述操作。
• 第二次迭代时 stride 为线程块大小的 1/4，即相加元素之间的距离是线程块大小的 1/4。
• …
• 最后一次迭代 stride 大小为1。

kernel 函数：

__global__ void reduceSum(double *d_A, int n){
    unsigned int t = threadIdx.x;
    __shared__ double partialSum[THREAD_LENGTH];
    if(blockIdx.x*blockDim.x + t < n)
        partialSum[t] = d_A[blockIdx.x*blockDim.x + t];
    else 
        partialSum[t] = 0;
    __syncthreads();  //将数组加载到共享存储器。
    for(unsigned int stride = blockDim.x / 2; stride > 0; stride /= 2){
        if(t < stride)
            partialSum[t] += partialSum[t + stride];
        __syncthreads();
    }
    if(t == 0)
        d_A[blockIdx.x*blockDim.x + t] = partialSum[t];
}

例如有 256 个线程的线程块计算 256 个元素的和，第一次迭代期间，线程 0 ~ 128执行加法语句，即warp 0~3 都执行加法语句，warp 4~7 都不执行加法运算，这就达到了一个 warp 中只有一个控制流路径的效果。但是后几步循环还是需要在一个 warp 中存在两个控制流路径的。

2.全局存储器的宽带

warp 加载数据与运行指令类似，如果一个 warp 的所有线程都执行一条加载指令时，如果这些线程访问的是全局存储器的连续内存单元，此时的访问效率最高，接近全局存储器宽带的峰值。

在介绍如何高效利用存储器宽带前，先来看一下 CUDA C 中多维数组的存储方式：

即以行序为主序

（二）中的简单矩阵乘法正好说明了两种最坏和最好的数组访问模式。

每个线程访问矩阵 d_M 的一行和 d_N 的一列。
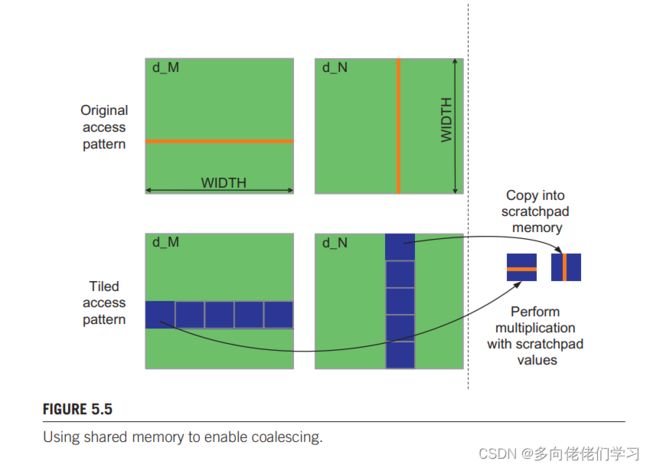
以 4x4 矩阵 d_M 与 4x4 的线程块为例，介绍d_M 的访问模式：

在第 0 次加载迭代中要访问 M_0,0，M_1,0，M_2,0， M_3,0 ，在第 1 次加载迭代中要访问 M_0,1，M_1,1，M_2,1， M_3,1 ，以此类推，每次加载迭代访问的四个数在内存中不是连续存放的，硬件就不能将这些访问加载成合并访问。

以 4x4 矩阵 d_N 与 4x4 的线程块为例，介绍d_ 的访问模式：

在第 k 次加载迭代中要访问 M_k,0，M_k,0，M_k,0， M_k,0 ，每次加载迭代访问的四个数在内存中是连续存放的，硬件就能将这些访问加载成合并访问。

所以，kernel 函数遍历一行的效率要远低于遍历一列的效率。

对于算法要求的必须按行读取矩阵元素时，可以使用共享存储器实现存储的合并访问。例如使用分块矩阵乘法：

__global__ void MatrixMulKernel(float *d_M, float *d_N, float *d_P, int m, int k, int n){
	__shared__ float Mds[TILE_WIDTH][TILE_WIDTH];
	__shared__ float Nds[TILE_WIDTH][TILE_WIDTH];
 	int bx = blockIdx.x;
	int by = blockIdx.y;
	int tx = threadIdx.x;
	int ty = threadIdx.y;

	int row = by * blockDim.y + ty;
	int col = bx * blockDim.x + tx;
    float Pvalue = 0;         //in every thread
    for(int ph = 0; ph < ceil(k/float(TILE_WIDTH));++ph){
        if(row < m && (ph * TILE_WIDTH + tx) < k)
            Mds[ty][tx] = d_M[row * k + ph * TILE_WIDTH + tx];
        else Mds[ty][tx] = 0.0;
        if(col < n && (ph * TILE_WIDTH + ty) < k)
            Nds[ty][tx] = d_N[(ph * TILE_WIDTH + ty) * n + col];
        else Nds[ty][tx] = 0.0;
        __syncthreads();
        for(int i = 0;i < TILE_WIDTH;++i){
            Pvalue += Mds[ty][i] * Nds[i][tx];
        }
        __syncthreads();
    }
    if (row < m && col < n)//将计算后的矩阵块放到结果矩阵d_P中
		d_P[row*n + col] = Pvalue;
}

14行按照索引公式d_M[row * k + ph * TILE_WIDTH + tx]，17行按照索引公式d_N[(ph * TILE_WIDTH + ty) * n + col] 从全局存储器中读取内容到块中。如果将 TILE_WIDTH 设置成与 warp 的大小相同的话， d_M 与 d_N 每个块中行的访问都可以通过 一个warp 完成。因为块内同一行的元素在在存储器中是连续存放的，所以同一个 warp 中的线程访问将被结合成一个合并的访问。
将块加载到共享存储器后，再对 d_M 的一块按行读取，对 d_N 的一块按行读取，因为共享存储器是高速的片上存储器，按行按列访问对访问速度没有影响。

3.执行资源的动态划分

SM 中的执行资源包括寄存器、共享存储器 、线程块槽和线程槽，这些资源冬天分配给线程。
例如一个 SM 有 8 个块槽，1536 个线程槽，如果每个线程块有 512 个线程，那么一个 SM 分配 3 个线程块，如果一个线程块有 128 个线程，那么一个 SM 分配 8 个块槽，共有1024个线程，这就是对线程槽的不充分利用。
另一个例子，我们知道 kernel 自动变量保存在寄存器中，在矩阵乘法中，假定每个 SM 包含 16384 个寄存器，每个线程用 10 个寄存器，每个块 16x16 个线程。则每个块中需要 2560个寄存器，6 个块需要用到 15360 个寄存器，7个块要用到 17920 个寄存器，超出限制，所以寄存器限制了每个线程块共有 6 个块，共有 1536 个线程在每个 SM 上运行。
假设在 kernel 中又声明了两个变量，现在每个块需要 12x16x16 = 3072 个寄存器。6个块需要 18432 个寄存器，只能在 SM 中减少一个块，那么一个 SM 就只有1280 个线程。多使用了两个寄存器，warp 的性能降低了 1/6。

所以在编写 kernel 函数时，要先了解硬件信息，以设计高效的 kernel 函数。