机器学习之 Logistic 回归算法及其 Python 实现

机器学习之 Logistic 回归算法及其 Python 实现

{% note info %}

如需要本文所用数据及代码原文件可留言评论。

{% endnote %}

前言：机器学习分类算法初步

感知器

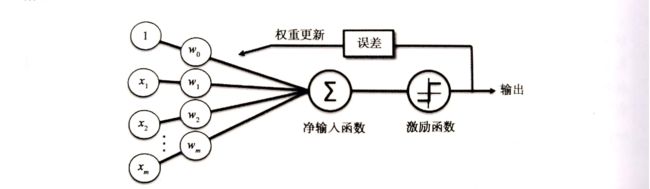
Frank Rossenblatt 基于 MCP 神经元模型提出第一个感知器学习法则。在此感知器规则中，自学习算法可以自动通过优化得到权重系数，雌蜥属与输入值的乘积决定了神经元是否被激活。在监督学习与分类中，类似算法课用于预测样本所属的类别。

对于一个二分类问题，我们将两个类别记为 1 （正类别）与 -1 （负类别）。定义一个激励函数（activation function）$\varphi (z)$ ，它以特定的输入值 $x$ 与相应的权值向量 $w$ 的线性组合作为输入，其中，$z$ 也称作净输入 $(z=w_1{x}_1+\cdots +w_m{x}_m)$。

此时，对于一个特定的样本 $x^{(i)}$ 的激励，也就是 $\varphi (z)$ 的输出，如果其值大于预设的阈值 $\theta$ ，我们将其划分到 1 类，否则为 -1 类。在感知器算法中，激励函数 $\varphi (\cdot )$ 是一个简单的分段函数。
$$\varphi (z)=\{\begin{array}{rl}1& 若z\ge \theta \\ -1& 其他\end{array}$$
MCP 神经元和罗森布拉特阈值感知器的理念就是，通过模拟的方式还原大脑中的单个神经元的工作方式。这样，罗森布拉特感知器最初的规则非常简单，可总结为如下几步：

1. 将权重初始化为零或一个极小的随机数。
2. 迭代所有的训练样本 $x^{(i)}$ ，执行如下操作：
   1. 计算输出值 $\hat{y}$ 。
   2. 更新权重。

这里的输出值是值通过前面定义的单位阶跃函数预测得出的类标，而这里的权重 $w$ 的更新方式为：
$$w_j=w_j+\Delta w_j$$
对于用于更新权重 $w_j$ 的值 $\Delta w_j$ ，可通过感知器学习规则计算获得：
$$\Delta w_j=\eta (y^{(i)}-{\hat{y}}^{(i)})x_j^{(i)}$$
其中，$\eta$ 为学习速率（一个介于 0 到 1 之间的常数），$y^{(i)}$ 为第 $i$ 个样本的真是类标，${\hat{y}}^{(i)}$ 为预测得到的类标。

自适应线性神经元及其学习的收敛性

在 Frank Rosenblatt 提出感知器算法纪念之后，Bernard Widrow 和他的博士生提出了 Adaline 算法，可看作对之前算法的改进。它阐明了代价函数的核心概念，并且对其做出了最小化优化，这是理解 Logistic 回归、支持向量机和后续回归模型的基础。

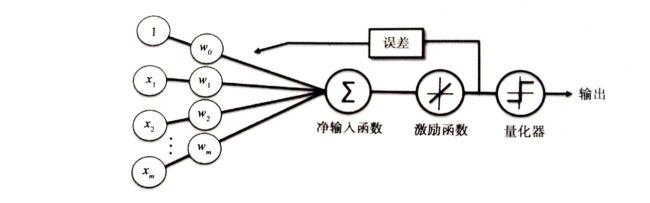
基于 Adeline 规则的权重更新是通过一个连续的线性激励函数来完成的，而不像感知器那样使用单位阶跃函数，这是二者的主要区别。

线性激励函数在更新权重同时，我们使用量化器对类标进行预测，量化器与前面提到的单位阶跃函数类似。

梯度下降法

机器学习中监督学习算法核心在于定义一个待优化的目标函数，这个目标函数通常是需要我们做最小化处理的代价函数。在 Adaline 中，我们可以将代价函数 $J$ 定义为通过模型得到的输出与实际类标之间的误差平方和：
$$J(w)=\frac{1}{2}\sum _i(y^{(i)}-\varphi (z^{(i)}){)}^2$$
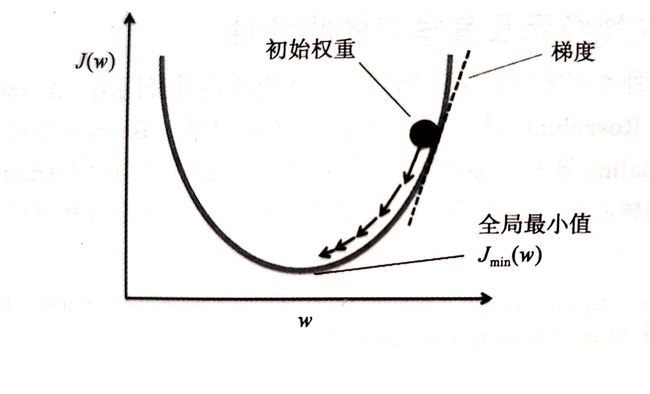
与单位阶跃函数相比，这种连续的线性激励函数的主要优点在于：其代价函数是可导的。另一个优点是：他是一个凸函数；这样，我们通过简单、高效的梯度下降优化算法；来得到权重。在每次迭代的过程中，根据给定的学习所率和梯度斜率，能够确定每次移动的步幅，我们按照步幅沿着梯度方向前进一步，直到获得一个局部或全局最小值：

$$ w:=w+\Delta w \\ \Delta w = -\eta \cfrac{\partial J}{\partial w_i} $$ 为了计算代价函数的梯度，我们需要计算代价函数相对于每个权重$w_j$ 的偏导$\cfrac{\partial J}{\partial w_i}$ 这样我们可以把 $w_j$ 的更新写作： $$ \Delta w_j=-\eta\cfrac{\partial J}{\partial w_i}=\mu\sum\limits_i(y^{(i)}-\phi(z^{(i)}))x_j^{(i)} $$

逻辑斯蒂（Logistic）回归

基本模型介绍

前言中提到的感知器是机器学习中优雅医用的一个入门级算 法，不过其最大的缺点在于：在样本不是完全线性可分的情况下，它永远不会收敛。为了提高分类效率，可以使用 Logistic 回归模型。注意：Logistic 回归模型是一个分类模型，而不是回归模型。

Logistic 回归是针对线性可分问题的一种易于实现且性能优异的分类模型。

设置激励函数：sigmoid 函数
$$\varphi (z)=\frac{1}{1+e^{-z}}$$
它的函数图像是这样的：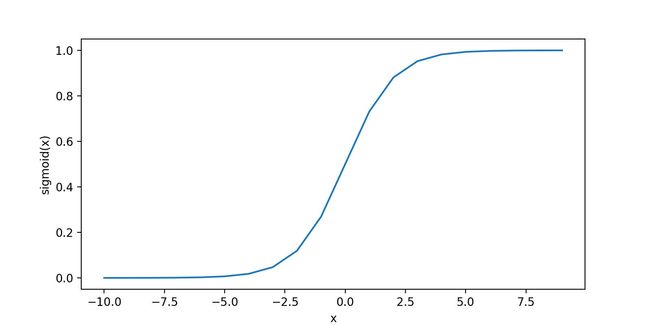

可以看到，当 $z$ 趋向于无穷大时，$\varphi (z)$ 趋近于 1，这是由于 $e^{-z}$ 在 $z$ 值极大的情况下变得极小。当$z$ 趋向于负无穷时，$\varphi (z)$ 趋近于 0，这是由于此时分母越来越大的结果。由此可以得出结论：

sigmoid 函数以实数值作为输入并将其映射到了 $[0,1]$ 区间，其拐点位于 $\varphi (z)=0.5$ 处。

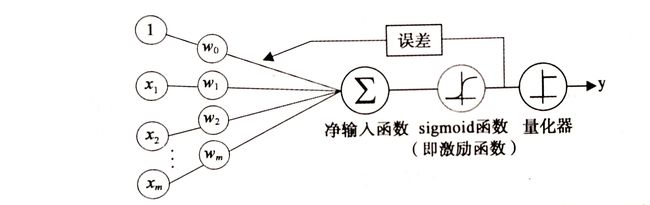
将 logistic 回归模型与上文中介绍的 Adaline 模型联系起来。在 Adaline 中，我们使用恒等函数 $\varphi (z)=z$ 作为激励函数。而在 logistic 回归模型中，只是简单地将前面提到的 sigmoid 函数作为激励函数，如下图所示：

在给定特征 x 及其权重 w 的权重情况下，sigmoid 函数的输出给出了特定的样本 x 所属的概率 $\varphi (z)=P(y=1|x;w)$。预测得到的概率可以通过量化器（单位跃阶函数）简单地转化为二元输出：
$$\hat{y}=\{\begin{array}{rl}1& 若\varphi (z)\ge 0.5\\ 0& 其他\end{array}$$
对照前面给出的 sigmoid 函数图像，它其实相当于：
$$\hat{y}=\{\begin{array}{rl}1& 若z\ge 0.0\\ 0& 其他\end{array}$$

通过代价函数获得权重

在 Adaline 分类模型中，我们定义其代价函数为误差平方和，根据此代价函数并运用梯度下降法更新权重，我们在构建 logistic 回归模型时，首先定义一个最大似然函数 $L$，其计算公式如下：
$$L(w)=P(y|x;w)=\prod _{i=1}^{n}P(y^{(i)}|x^{(i)};w)={\left(\varphi \left(z^{(i)}\right)\right)}^{y^{(i)}}{\left(1-\varphi \left(x^{(i)}\right)\right)}^{1-y^{(i)}}$$
作对数化处理后：
$$\ln L(w)=\sum _{i=1}^n\left(y^{(i)}\ln \left[\varphi \left(z^{(i)}\right)\right]+\left(1-y^{(i)}\right)\ln \left[1-\varphi \left(z^{(i)}\right)\right]\right)$$
根据前文提到的梯度下降法做代价函数的最小化处理，求解权重。

logistic 的 Python 实现

实现方式一：不使用机器学习第三方库

# -*- coding:utf-8 -*-
"""
@author:Lisa
@file:logisticRegression.py
@note:logistic回归
@time:2018/7/11 0011下午 10:45
"""

import numpy as np
import matplotlib.pyplot as plt


def loadDataSet():
    """
    函数：加载数据集
    """
    dataMat = []  # 列表list
    labelMat = []
    txt = open('testSet.txt')
    for line in txt.readlines():
        lineArr = line.strip().split()
        # strip():返回一个带前导和尾随空格的字符串的副本
        # split():默认以空格为分隔符，空字符串从结果中删除
        dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])  # 将二维特征扩展到三维，第一维都设置为1.0
        labelMat.append(int(lineArr[2]))

    return dataMat, labelMat


"""
函数：sigmoid函数
"""
def sigmoid(z):
    return 1.0/(1+np.exp(-z))

"""
函数：梯度上升算法
"""
def gradAscent(dataMat, labelMat):
    dataSet = np.mat(dataMat)                          # m*n
    labelSet = np.mat(labelMat).transpose()            # 1*m->m*1
    m, n = np.shape(dataSet)                            # m*n: m个样本，n个特征
    alpha = 0.001                                      # 学习步长
    maxCycles = 500                                    # 最大迭代次数
    weights = np.ones((n, 1))
    for i in range(maxCycles):
        y = sigmoid(dataSet * weights)                 # 预测值
        error = labelSet - y
        weights = weights + alpha * dataSet.transpose()*error
    #print(type(weights))
    return weights.getA(),weights  ##getA():将Mat转化为ndarray,因为mat不能用index

"""
函数：随机梯度上升算法0.0
改进：每次用一个样本来更新回归系数
"""
def stocGradAscent0(dataMat,labelMat):
    m, n = np.shape(dataMat)  # m*n: m个样本，n个特征
    alpha = 0.001  # 学习步长
    maxCycles=500
    weights = np.ones(n)
    for cycle in range(maxCycles):
        for i in range(m):
            y = sigmoid(sum(dataMat[i] * weights) )  # 预测值
            error = labelMat[i] - y
            weights = weights + alpha  * error* dataMat[i]
        # print(type(weights))
    return weights


"""
函数：改进的随机梯度上升法1.0
改进：1.alpha随着迭代次数不断减小，但永远不会减小到0
     2.通过随机选取样本来更新回归系数
"""
def stocGradAscent1(dataMat,labelMat):

    m, n = np.shape(dataMat)  # m*n: m个样本，n个特征
    maxCycles = 150
    weights = np.ones(n)
    for cycle in range(maxCycles):
        dataIndex=list( range(m))
        for i in range(m):
            alpha = 4 / (1.0 + cycle + i) + 0.01                 # 学习步长
            randIndex=int(np.random.uniform(0,len(dataIndex) ))  #随机选取样本
            y = sigmoid(sum(dataMat[randIndex] * weights ))          # 预测值
            error = labelMat[randIndex] - y
            weights = weights + alpha  * error * dataMat[randIndex]
            del(dataIndex[randIndex])
            # print(type(weights))
    return weights


"""
函数：画出决策边界
"""
def plotBestFit(weights):
    dataMat, labelMat = loadDataSet()
    dataArr=np.array(dataMat)
    m,n=np.shape(dataArr)
    x1=[]           #x1,y1:类别为1的特征
    x2=[]           #x2,y2:类别为2的特征
    y1=[]
    y2=[]
    for i in range(m):
        if (labelMat[i])==1:
            x1.append(dataArr[i,1])
            y1.append(dataArr[i,2])
        else:
            x2.append(dataArr[i,1])
            y2.append(dataArr[i,2])
    fig=plt.figure()
    ax=fig.add_subplot(1,1,1)
    ax.scatter(x1,y1,s=30,c='red',marker='s')
    ax.scatter(x2,y2,s=30,c='green')

    #画出拟合直线
    x=np.arange(-3.0, 3.0, 0.1)
    y=(-weights[0]-weights[1]*x)/weights[2]    #直线满足关系：0=w0*1.0+w1*x1+w2*x2
    ax.plot(x,y)

    plt.xlabel('X1')
    plt.ylabel('X2')
    plt.show()


def main():
    dataMat,labelMat=loadDataSet()
    weights = gradAscent(dataMat,labelMat)[0]
    weights = stocGradAscent0(np.array(dataMat), labelMat)
    weights = stocGradAscent1(np.array(dataMat), labelMat)
    plotBestFit(weights)


if __name__ == '__main__':
    main()

运行结果：

实现方式二：使用 sklearn 模块

模块介绍：

sklearn.linear_model.LogisticRegression官方API：
官方API：http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html

class sklearn.linear_model.LogisticRegression (penalty='l2', dual=False, tol=0.0001, C=1.0,fit_intercept=True, intercept_scaling=1, class_weight=None, random_state=None,solver='liblinear', max_iter=100, multi_class='ovr', verbose=0,warm_start=False, n_jobs=1)

参数说明：

• penalty：

惩罚项，可为’l1’ or ‘l2’。‘netton-cg’, ‘sag’, ‘lbfgs’只支持’l2’。‘l1’正则化的损失函数不是连续可导的，而’netton-cg’, ‘sag’, 'lbfgs’这三种算法需要损失函数的一阶或二阶连续可导。调参时如果主要是为了解决过拟合，选择’l2’正则化就够了。若选择’l2’正则化还是过拟合，可考虑’l1’正则化。若模型特征非常多，希望一些不重要的特征系数归零，从而让模型系数化的话，可用’l1’正则化。
dual：选择目标函数为原始形式还是对偶形式。
将原始函数等价转化为一个新函数，该新函数称为对偶函数。对偶函数比原始函数更易于优化。

• tol：

优化算法停止的条件。当迭代前后的函数差值小于等于tol时就停止。

• C：

正则化系数。其越小，正则化越强。

• fit_intercept：

选择逻辑回归模型中是否会有常数项b

• intercept_scaling：

仅在正则化项为"liblinear"，且fit_intercept设置为True时有用。

• class_weight：

用于标示分类模型中各种类型的权重，{class_label: weight} or ‘balanced’。

1. ‘balanced’：类库根据训练样本量来计算权重。某种类型的样本量越多，则权重越低。

2. 若误分类代价很高，比如对合法用户和非法用户进行分类，可适当提高非法用户的权重。

3. 样本高度失衡的。如合法用户9995条，非法用户5条，可选择’balanced’，让类库自动提高非法用户样本的权重。

• random_state：

随机数种子。

• solver：

逻辑回归损失函数的优化方法。

1. **‘liblinear’：**使用坐标轴下降法来迭代优化损失函数。

2. ‘lbfgs’： 拟牛顿法的一种。利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。

3. **‘newton-cg：’**牛顿法的一种。同上。

4. **‘sag’：**随机平均梯度下降。每次迭代仅仅用一部分的样本来计算梯度，适合于样本数据多的时候。
   多元逻辑回归有OvR(one-vs-rest)和MvM(many-vs-many)两种，而MvM一般比OvR分类相对准确一些。但是，'liblinear’只支持OvR。

• max_iter：

优化算法的迭代次数。

• multi_class：

‘ovr’ or ‘multinomial’。'multinomial’即为MvM。

  1. 若是二元逻辑回归，二者区别不大。

  2. 对于MvM，若模型有T类，每次在所有的T类样本里面选择两类样本出来，把所有输出为该两类的样本放在一起，进行二元回归，得到模型参数，一共需要T(T-1)/2次分类。

• verbose：

控制是否 print 训练过程。

• warm_start：
  是否热启动，如果是，则下一次训练是以追加树的形式进行（重新使用上一次的调用作为初始化），bool：热启动，False：默认值

• n_jobs：

用cpu的几个核来跑程序。

demo

# -*- coding:utf-8 -*-
"""
@author:Lisa
@file:sklearn_horse_colic.py
@note:利用sklearn的LR方法实现 疝气马预测
@time:2018/7/13 0013上午 11:30
@reference:
"""

from sklearn.linear_model import LogisticRegression

"""
函数：疝气预测
"""
def colicTest():
    trainData=open('data\horseColicTraining.txt')
    testData = open('data\horseColicTest.txt')
    trainSet=[]
    trainLabel=[]
    for line in trainData.readlines():
        curLine=line.strip().split('\t')
        lineArr=[]
        for i in range(21):
            lineArr.append(float (curLine[i]))
        trainSet.append(lineArr)
        trainLabel.append(float(curLine[21]))


    testSet = []
    testLabel = []
    for line in testData.readlines():
        curLine=line.strip().split('\t')
        lineArr=[]
        for i in range(21):
            lineArr.append(float (curLine[i]))
        testSet.append(lineArr)
        testLabel.append(float(curLine[21]))
    #分类器
    classifier = LogisticRegression(solver='sag', max_iter=5000).fit(trainSet, trainLabel)
    test_accurcy = classifier.score(testSet, testLabel) * 100
    print("the accurate rate is: %f" % test_accurcy)

运行结果：

the accurate rate is: 73.134328

实现方式三：使用 Pytorch 模块

import torch
import torch.nn as nn
import matplotlib.pyplot as plt
import numpy as np
torch.manual_seed(10)
 
 
# ============================ step 1/5 生成数据 ============================
sample_nums = 100
mean_value = 1.7
bias = 1
n_data = torch.ones(sample_nums, 2)
x0 = torch.normal(mean_value * n_data, 1) + bias      # 类别0 数据 shape=(100, 2)
y0 = torch.zeros(sample_nums)                         # 类别0 标签 shape=(100, 1)
x1 = torch.normal(-mean_value * n_data, 1) + bias     # 类别1 数据 shape=(100, 2)
y1 = torch.ones(sample_nums)                          # 类别1 标签 shape=(100, 1)
train_x = torch.cat((x0, x1), 0)
train_y = torch.cat((y0, y1), 0)
 
 
# ============================ step 2/5 选择模型 ============================
class LR(nn.Module):
    def __init__(self):
        super(LR, self).__init__()
        self.features = nn.Linear(2, 1)
        self.sigmoid = nn.Sigmoid()
 
    def forward(self, x):
        x = self.features(x)
        x = self.sigmoid(x)
        return x
 
 
lr_net = LR()   # 实例化逻辑回归模型
 
 
# ============================ step 3/5 选择损失函数 ============================
loss_fn = nn.BCELoss()
 
# ============================ step 4/5 选择优化器   ============================
lr = 0.01  # 学习率
optimizer = torch.optim.SGD(lr_net.parameters(), lr=lr, momentum=0.9)
 
# ============================ step 5/5 模型训练 ============================
for iteration in range(1000):
 
    # 前向传播
    y_pred = lr_net(train_x)
 
    # 计算 loss
    loss = loss_fn(y_pred.squeeze(), train_y)
 
    # 反向传播
    loss.backward()
 
    # 更新参数
    optimizer.step()
 
    # 清空梯度
    optimizer.zero_grad()
 
    # 绘图
    if iteration % 20 == 0:
 
        mask = y_pred.ge(0.5).float().squeeze()  # 以0.5为阈值进行分类
        correct = (mask == train_y).sum()  # 计算正确预测的样本个数
        acc = correct.item() / train_y.size(0)  # 计算分类准确率
 
        plt.scatter(x0.data.numpy()[:, 0], x0.data.numpy()[:, 1], c='r', label='class 0')
        plt.scatter(x1.data.numpy()[:, 0], x1.data.numpy()[:, 1], c='b', label='class 1')
 
        w0, w1 = lr_net.features.weight[0]
        w0, w1 = float(w0.item()), float(w1.item())
        plot_b = float(lr_net.features.bias[0].item())
        plot_x = np.arange(-6, 6, 0.1)
        plot_y = (-w0 * plot_x - plot_b) / w1
 
        plt.xlim(-5, 7)
        plt.ylim(-7, 7)
        plt.plot(plot_x, plot_y)
 
        plt.text(-5, 5, 'Loss=%.4f' % loss.data.numpy(), fontdict={'size': 20, 'color': 'red'})
        plt.title("Iteration: {}\nw0:{:.2f} w1:{:.2f} b: {:.2f} accuracy:{:.2%}".format(iteration, w0, w1, plot_b, acc))
        plt.legend()
 
        plt.show()
        plt.pause(0.5)
 
        if acc > 0.99:
            break

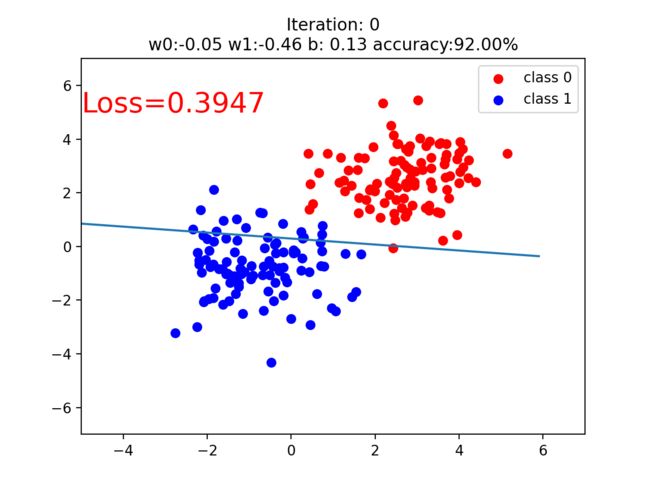
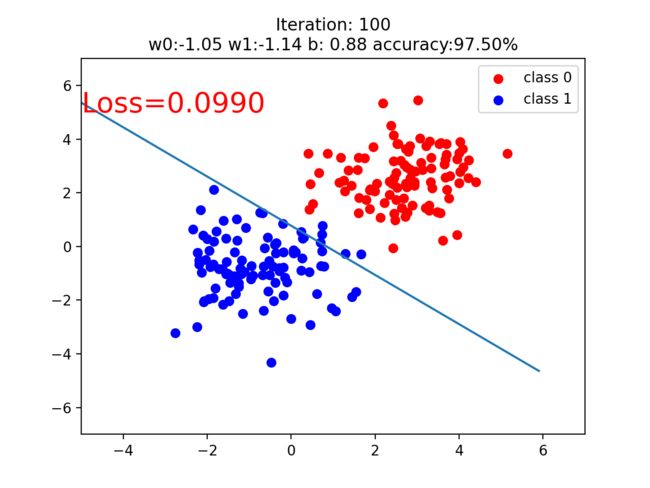
参考博文:

logistic回归原理与实现

Sklearn-LogisticRegression逻辑回归

sklearn 官方API

Pytorch：通过pytorch实现逻辑回归