KMP算法真的有这么难吗？（清晰详细版）

KMP算法我一年之前就接触了，但由于实在难以理解next[]求法故放弃，每次做一次字符串匹配的时候，很多情况下都是暴力解决，除了极个别情况把next[]求法背成模板求解AC。
注意：KMP算法已经成为了数据结构考研大纲中了。

最近由于是刷题，再一次碰到了KMP算法，同时学院课程《算法设计与分析》也探讨了KMP算法，这让我不得不进行重新思考。翻遍大量的资料，其中就有CSDN传播最广的文章，有兴趣的可以查看从头到尾彻底理解KMP（2014年8月22日版）但是上面博客实在是太长了，虽然很好，但是看起来真的很吃力。特别是一开始就给你KMP定义让人很难读下去。同时也很有很多博客，一开始就给你next[]的定义，非常突兀。

本篇博客立足于算法初学者，从预备知识到next数组的引出，再到推导公式，最后给出代码**。这是一篇快速掌握并且十分简洁的KMP算法博客。**

我了解到next[]代码部分和手写next[]根本就不是一个思路。很多教辅也只会教手写部分，但手写next[]主要是进行比较前后缀最大相等长度，但是代码部分就根本没有这一思想，主要是数学归纳与推导证明，个人感觉，十分具有挑战性，毕竟我本人光next[]也看了很久。所以，一开始接触kmp，特别是企图求next数组的不要担心与焦虑，这将是一篇让你彻底明白为什么有next[]以及kmp原理等的博客。

希望本篇博客对你有所帮助！

简单的模式匹配

字串定位为串的模式匹配，求的是子串（常称为模式串）在主串的位置。以下是暴力求法，这是数据结构中关于string的定义：

#define MAXLEN 255
typedef struct{
	char ch[MAXLEN];
	int length;
}SString;

int index(SString s,SString t){
	int i=1,j=1;
	while(i<= s.length && j<= t.length){
		if(s.ch[i] == t.ch[i]){
			++i;
			++j;
		} else {
			i = i-j+2; //回溯了
			j = 1;
		}
	}
	if(j>t.length) return i - t.length;
	else return 0;
}

时间复杂度为O(mn).m,n分别表示两个字符串的长度。

KMP算法

根据上面的暴力算法，我们不难发现很多比较都是重复的，为什么呢？请看下面这个例子：

S = "abcdasfabce";
T = "abce"

按照上面暴力的方法
S需要回溯，但是人很容易通过肉眼看出可以不用回溯，只需要在
S = "abcdasfabce"
T = "abce"
和
T =         "abce"
这两处比较就可以了（中间省略了很多比较，主要是让大家了解主串不回回溯）

这里主要是引子，让大家知道很多比较是重复的了，接下来我们需要有一些预备的知识。

前缀后缀部分匹配

首先要理解KMP，必须要对前缀，后缀，部分匹配有认识。这里以’ababa‘为例：
注意的是，前缀就是从左往右的子串；后缀不是从最后开始从右往左，而是从最后开始的从左往右子串。
ababa的子串共有a,ab,aba,abab.注意ababa不是子串。
这里规定pre:前缀 suf:后缀 len:最长相等前后缀长度
对于a,pre,suf: null len:0 .(规定前缀是子串，所以a不是a的子串）
对于ab, pre:a suf:b , pre∩suf = null len :0
对于aba, pre:a,ab suf :a,ba pre∩suf = a len:1;
以此类推：abab:len为2；ababa:len为3
这里说一下ababa suf: a,ba,aba,baba pre :a,ab,aba,abab 所以pre∩suf = aba ,len=3
所以我们就有了ababa的部分匹配值为00123.

有了这个值可以做什么呢？

部分匹配值的作用

现在假设主串为 ababcabcacbab 子串为abcac
根据前面的方法，我们可以求出子串的部分匹配值为： 00010，下面将进行手工匹配
公式1 ： 移动位数 = 已匹配的字符数 - 对应的部分匹配值
公式不理解不要紧，可以接着往下看的样例。

//第一趟：
s = "ababcabcacbab"
t = "abc.." //从不匹配的开始就用省略号代替了。
此时发现c位不匹配，根据匹配值最后一个匹配字符b对应的为0,那么根据公式1：移动位数= 2-0 = 2，所以此时子串向后移动2位，注意此时s的指针（相当于遍历变量i)是不回溯的，依旧接着走
此时s与t的位置：
s = "ababcabcacbab"
t =   "abcac"

//第二趟：
发现第5位c是不匹配的了，接着上面的操作，移动位数 = 4-1（最后匹配字符的匹配值） = 3。此时位置如下：
s = "ababcabcacbab"
t =      "abcac"
此时匹配成功

以上就是kmp的模式匹配，我们注意到主串指针（遍历i)始终没有回溯，一直在往前走，这是很重要的思想。所以，很明显，kmp的时间复杂度就算O(m+n)，m,n分别为主串子串的长度。

KMP原理

相信很多人对上述公式1很迷惑吧。公式1 ： 移动位数 = 已匹配的字符数 - 对应的部分匹配值
以下图为例：在第二行子串，b与c不匹配。已匹配的abca 的前缀a,后缀a是最长公共元素。那么a与b,c又不同，肯定直接把a移到第二个a的时候才有可能匹配，而这个移动的位数就是上面的公式。这个目的就是在子串先找相同的前后缀，然后直接把子串移到相同的后缀处。

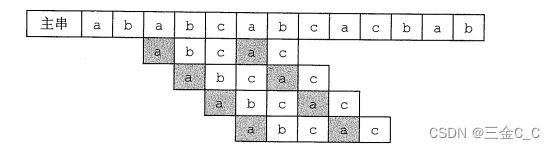
next数组

已知： 右移位数 = 已匹配的字符数 - 对应的部分匹配值
使用部分匹配值的时候，每当匹配失败需要寻找前一个元素的部分匹配值，这样使用起来不方便，所以我们可以将匹配值数组全部右移一位，就得到了next数组了。
以abcac的部分匹配值 00010为例
那么它的next数组数就是全部右移一位：就是-1 0 0 0 1
我们注意到：
1.第一位右移后需要用-1来代替。因为第一个元素失败了，根据公式 0 - （-1）才等于1，符合第一位不匹配向右移一位的常识。
2.最后一个元素在右移过程中会溢出（右移没有它了），很明显，最后一个元素的部分匹配值是给下一个元素使用的，但是没有下一个了所以可以舍去。

那么上述公式就可以写成 ： 右移位数 = 已匹配字符数 - 改位置j的next[j]
那么就有公式： Move = (j-1) - next[j]
那么我们觉得前面j-1不好看，还可以再优化，从上述公式可以得到：
Move = j - (next[j] +1)，那么我可以把next[j]全部加上1.
什么意思呢？
还是以abcac为例，他之前我们算的next就是 -1 0 0 0 1
根据优化，现在他的next就是 0 1 1 1 2.
那么我们就得到了子串指针的公式：
j = next[j]
next[j]是什么意思呢？在子串的第j个字符与主串发生不匹配的时候，那么就跳到next[j]位置重新与主串进行比较。

推导next[]公式

如何推导next的公式呢？主串为s1s2s3…sn ,模式串p1p2…pm。当主串第i个字符与模式串第j个字符不匹配的时候，子串应该向右滑动多远呢？
假设此时与模式串的第k (k 串：p1p2…pk-1 = pj-k+1 pj-k+2 … pj-1 （）
见下图说明，阴影部分就是匹配相等。

如果满足上述（） 子串，如果发生不匹配，根据前面所说的，那么只需要模式串p1移动到pj-k+1处（见上图）

注意，下面的j不是指模式串的长度，而就是遍历模式串的指针j!!!

那么我们就得到以下公式了：
next[]公式
next[j] = 0 j =1
next[j] = max{k | 1 next[j] =1 ,其他情况

那么有了公式，问题就转换成已知next[1]= 0 (为什么是0，因为前面我右移了一位并且都加1，索引从1开始主要是为了方便），设next[j]=k,k就是上面的条件中的k.
那么next[j+1]等于多少呢？
很明显的数归法的感觉（对不对呢）

现在对于指针j+1的情况有两种：

1. pk = pj
   这个什么意思呢？
   之前有式子： p1p2…pk-1 = pj-k+1 pj-k+2 … pj-1 （k必须满足这个条件，题目已经列出）
   现在再加上这个条件p1p2…pk-1 pk = pj-k+1 pj-k+2 … pj-1 pj
   这个已经很明显了。类似于整体代换：next[j+1] = k+1
2. pk != pj
   那么和上面一样：
   再加上这个条件p1p2…pk-1 pk != pj-k+1 pj-k+2 … pj-1 pj
   那么这个问题就可以转变成 用p1…pk去和后缀pj-k+1…pj匹配，什么意思呢，有没有套娃的感觉。
   是的，这一步思想就是套娃，理论推导较为复杂，下面以一个例子为例：

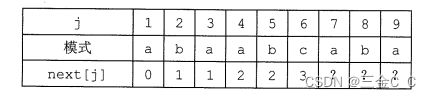
现在我们如何算next[7]呢？
因为next[6]=3,但是p6 != p3,那么比较p6 和 p1（因为next[3]=1) ,但是p6 != p1,而next[1]=0,所以根据前面next公式，next[7]=1了。

到这里你会自己求next[8]了吗？
要想求next[8],那么next[7] = 1,p7 == p1,所以next[8] = next[7] +1 =2 (这里就是我们之前pk = pj的情况啦）
同理next[9] = 3
下面根据代码好好理解一下：

代码部分

void get_next(SString t,int next){
	int i=1,j=0;
	next[1]=0;
	while(i<t.length){
		if(j==0 || t.ch[i] == t.ch[j) {
			++i;
			++j;
			next[i] = j;
		}else {
			j = next[j]; //循环继续
			}
	}
}

这个就是模式串的next求法了。
kmp匹配算法就很简单了，甚至就是前面比起来就是小巫见大巫了。

int KMP(SString s,SString t,int next[]) {
	int i=1,j=1;
	while(i<s.length&& j<t.length){
		if(j==0 || s.ch[i] == t.ch[j]) {
			++i;
			++j; //匹配那就继续比较
			
		}else {
			j = next[j];//模式串向右移动
		}
	}
	if(j>t.length) return i - t.length;
	else return 0;
}

优化KMP算法

在前面定义的next数组在某些情况下尚有缺陷，仍有优化的空间。

如上图所示，i=4 s4与p4失配，如果使用之前的next那么还要进行s4与p3,s4与p2,s4与p1三次比较（想想为什么？那当然是右移操作了）
但是，后面的三次比较毫无意义.
这里提高一个nextval代码，但是不做解释了,看代码很容易理解。

void get_nextval(SString t,int nextval[]){
	int i=1,j=0;
	nextval[1] = 0;
	while(i < t.length) {
		if(j == 0 || t.ch[i] == t.ch[j]){
			++i;
			++j;
			if(t.ch[i] != t.ch[j]) nextval[i] = j;
			else nextval[i] = nextval[j];
		}else {
		j = nextval[j];
	}
	}
}