滑动窗口算法基本原理

学过计算机网络的同学，都知道滑动窗口协议（Sliding Window Protocol），该协议是 TCP协议 的一种应用，用于网络数据传输时的流量控制，以避免拥塞的发生。该协议允许发送方在停止并等待确认前发送多个数据分组。由于发送方不必每发一个分组就停下来等待确认。因此该协议可以加速数据的传输，提高网络吞吐量。

滑动窗口算法其实和这个是一样的，只是用的地方场景不一样，可以根据需要调整窗口的大小，有时也可以是固定窗口大小。

滑动窗口算法在一个特定大小的字符串或数组上进行操作，而不在整个字符串和数组上操作，这样就降低了问题的复杂度，从而也达到降低了循环的嵌套深度。其实这里就可以看出来滑动窗口主要应用在数组和字符串上。

示例

如下图所示，设定滑动窗口（window）大小为 3，当滑动窗口每次划过数组时，计算当前滑动窗口中元素的和，得到结果 res。

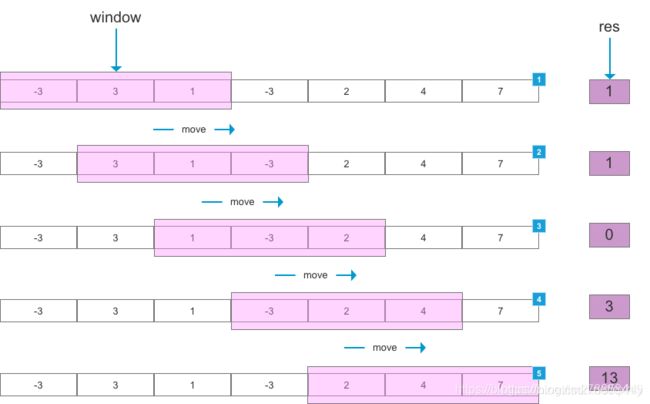
可以用来解决一些查找满足一定条件的连续区间的性质（长度等）的问题。由于区间连续，因此当区间发生变化时，可以通过旧有的计算结果对搜索空间进行剪枝，这样便减少了重复计算，降低了时间复杂度。往往类似于“ 请找到满足 xx 的最 x 的区间（子串、子数组）的 xx ”这类问题都可以使用该方法进行解决。

需要注意的是，滑动窗口算法更多的是一种思想，而非某种数据结构的使用。

滑动窗口法的大体框架

在介绍滑动窗口的框架时候，大家先从字面理解下：
滑动：说明这个窗口是移动的，也就是移动是按照一定方向来的。
窗口：窗口大小并不是固定的，可以不断扩容直到满足一定的条件；也可以不断缩小，直到找到一个满足条件的最小窗口；当然也可以是固定大小。

为了便于理解，这里采用的是字符串来讲解。但是对于数组其实也是一样的。滑动窗口算法的思路是这样：

• 我们在字符串 S 中使用双指针中的左右指针技巧，初始化 left = right = 0，把索引闭区间 [left, right] 称为一个「窗口」。
• 我们先不断地增加 right 指针扩大窗口 [left, right]，直到窗口中的字符串符合要求（包含了 T 中的所有字符）。
• 此时，我们停止增加 right，转而不断增加 left 指针缩小窗口 [left, right]，直到窗口中的字符串不再符合要求（不包含 T 中的所有字符了）。同时，每次增加 left，我们都要更新一轮结果。
• 重复第 2 和第 3 步，直到 right 到达字符串 S 的尽头。

第 2 步相当于在寻找一个「可行解」，然后第 3 步在优化这个「可行解」，最终找到最优解。左右指针轮流前进，窗口大小增增减减，窗口不断向右滑动。

对于非固定大小的滑动窗口，可以简单地写出如下伪码框架：

string s, t;
    // 在 s 中寻找 t 的「最小覆盖子串」
    int left = 0, right = 0;
    string res = s;
    
    while(right < s.size()) {
        window.add(s[right]);
        right++;
        // 如果符合要求，说明窗口构造完成，移动 left 缩小窗口
        while (window 符合要求) {
            // 如果这个窗口的子串更短，则更新 res
            res = minLen(res, window);
            window.remove(s[left]);
            left++;
        }
    }
    return res;

对于固定窗口大小，可以总结如下：

// 固定窗口大小为 k
    string s;
    // 在 s 中寻找窗口大小为 k 时的所包含最大元音字母个数
    int  right = 0;
    while(right < s.size()) {
        window.add(s[right]);
        right++;
        // 如果符合要求，说明窗口构造完成，
        if (right>=k) {
            // 这是已经是一个窗口了，根据条件做一些事情
           // ... 可以计算窗口最大值等 
            // 最后不要忘记把 right -k 位置元素从窗口里面移除
        }
    }
    return res;

• 可以发现此时不需要依赖 left 指针了。因为窗口固定所以其实就没必要使用left，right 双指针来控制窗口的大小。
  其次是对于窗口是固定的，可以轻易获取到 left 的位置，此处 left = right-k;

算法实例

尽可能使字符串相等
给你两个长度相同的字符串，s 和 t。

将 s 中的第 i 个字符变到 t 中的第 i 个字符需要 |s[i] - t[i]| 的开销（开销可能为 0），也就是两个字符的 ASCII 码值的差的绝对值。

用于变更字符串的最大预算是 maxCost。在转化字符串时，总开销应当小于等于该预算，这也意味着字符串的转化可能是不完全的。

如果你可以将 s 的子字符串转化为它在 t 中对应的子字符串，则返回可以转化的最大长度。

如果 s 中没有子字符串可以转化成 t 中对应的子字符串，则返回 0。

输入：s = “abcd”, t = “bcdf”, cost = 3
输出：3
解释：s 中的 “abc” 可以变为 “bcd”。开销为 3，所以最大长度为 3。

class Solution {
    public int equalSubstring(String s, String t, int maxCost) {
        int left = 0, right =0;
        int sum = 0;
        int res = 0;　　　　 // 构造窗口
        while (right < s.length()) {
            sum += Math.abs(s.charAt(right) - t.charAt(right));
            right++;　　　　　　　// 窗口构造完成，这时候要根据条件当前的窗口调整窗口大小
            while (sum > maxCost) {
                sum -=  Math.abs(s.charAt(left) - t.charAt(left));
                left++;
            }　　　　　　　// 记录此时窗口的大小
            res = Math.max(res, right -left);
        }
        return res;
    }
}