前缀树及AC自动机
前缀树
前缀树也就是字典树,Trie树
力扣上就有这么一题让你实现前缀树,咱直接看这题:208. 实现 Trie (前缀树)
Trie(发音类似 "try")或者说 前缀树 是一种树形数据结构,用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景,例如自动补完和拼写检查。
请你实现 Trie 类:
Trie() 初始化前缀树对象。
void insert(String word) 向前缀树中插入字符串 word 。
boolean search(String word) 如果字符串 word 在前缀树中,返回 true(即,在检索之前已经插入);否则,返回 false 。
boolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix ,返回 true ;否则,返回 false 。
class Trie {
public Trie() {
}
public void insert(String word) {
}
public boolean search(String word) {
}
public boolean startsWith(String prefix) {
}
}
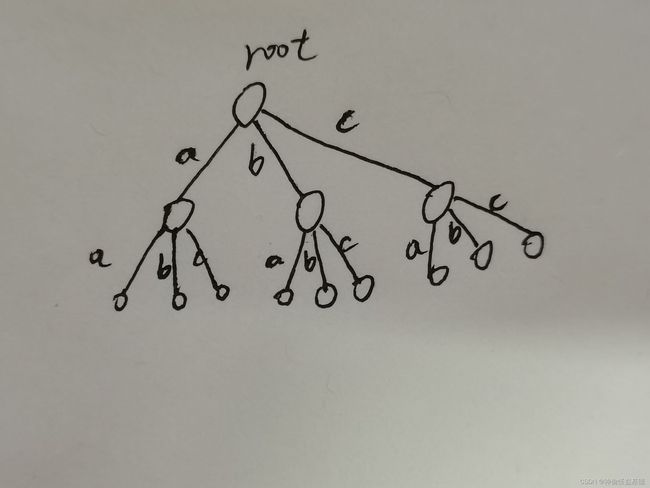
我们先来看看前缀树的结构
这里每个节点下其实是有26个分支的(当然如果不止英文字母的话可以根据自己的需求设计分支的数量,本文中的是只有英文的,也就26个分支),至于 'a'、'b'、'c' 这些字符是不需要存进节点中的,只要在节点中搞一个节点数组nexts,大小为26,那么 nexts[0]~nexts[25] 就分别对应 a~z
节点:
static class Node {
private boolean isEnd; //用于记录当前节点是否表示插入字符串的尾节点
private Node[] nexts = new Node[26];
}代码很好理解,我们直接看代码
class Trie {
static class Node {
private boolean isEnd;
private Node[] nexts = new Node[26];
}
Node root = new Node();
public Trie() {}
// 对于这道题来说,题目已经明确说了 1 <= word.length, prefix.length <= 2000 了,
// 我们就不需要 校验传入参数 word 和 prefix 的合法性了
public void insert(String word) {
char[] str = word.toCharArray();
Node cur = root;
for (char c : str) {
int index = c - 'a';
if (cur.nexts[index] == null) {
cur.nexts[index] = new Node();
}
cur = cur.nexts[index];
}
cur.isEnd = true;
}
public boolean search(String word) {
Node cur = goToLast(word);
//return cur == null ? false : cur.isEnd; 可以下面这样简单点
return cur != null && cur.isEnd;
}
public boolean startsWith(String prefix) {
return goToLast(prefix) != null; // 能沿着prefix走完就必然存在该前缀
}
// 沿着s顺着前缀树往下走
// 返回代表s最后一个字符的节点
public Node goToLast(String s) {
char[] str = s.toCharArray();
Node cur = root;
for (char c : str) {
int index = c - 'a';
// 如果沿着s还没走完就为null了,那直接返回null
if (cur.nexts[index] == null) {
return null;
}
cur = cur.nexts[index];
}
return cur;
}
}
上面那种实现是一个基本的结构,当我们要实现其它一些功能(返回插入过的字符串中出现了几次 word,出现了几次 prefix,删除字符串)的时候就可以用下面这种结构了
节点:
class Node {
int pass; //用于记录有多少个字符串经过了该节点
int end; //用于记录有多少个字符串以当前节点结尾
Node[] nexts = new Node[26];
}代码实现:
class Trie {
static class Node {
int pass; //用于记录有多少个字符串经过了该节点
int end; //用于记录有多少个字符串以当前节点结尾
Node[] nexts = new Node[26];
}
Node root = new Node();
public Trie() {}
public void insert(String word) {
if (word == null || word.length() == 0) {
return;
}
char[] str = word.toCharArray();
Node cur = root;
for (char c : str) {
int index = c - 'a';
if (cur.nexts[index] == null) {
cur.nexts[index] = new Node();
}
cur = cur.nexts[index];
cur.pass++;
}
cur.end++;
}
// 返回以前插入的word里面出现多少次当前要查的word
public int searchPro(String word) {
Node cur = goToLast(word);
return cur == null ? 0 : cur.end;
}
// 返回以前插入的word里面出现多少次prefix前缀
public int startsWithPro(String prefix) {
Node cur = goToLast(prefix);
return cur == null ? 0 : cur.pass;
}
// 沿着前缀树往下走
public Node goToLast(String s) {
if (s == null || s.length() == 0) {
return null;
}
char[] str = s.toCharArray();
Node cur = root;
for (char c : str) {
int index = c - 'a';
if (cur.nexts[index] == null) {
return null;
}
cur = cur.nexts[index];
}
return cur;
}
// 实现删除功能
public void delete(String word) {
if (searchPro(word) == 0) { // 如果都没有 word 的话删个毛啊
return;
}
Node cur = root;
char[] str = word.toCharArray();
for (char c : str) {
int index = c - 'a';
// 如果要去的节点pass减完后都等于0了那就没有必要再走了
if (--cur.nexts[index].pass == 0) {
cur.nexts[index] = null;
return;
}
cur = cur.nexts[index];
}
cur.end--;
}
}
AC自动机
作用:一篇大文章 str,一个包含若干敏感词的词典 str[],收集文章中所有出现的敏感词
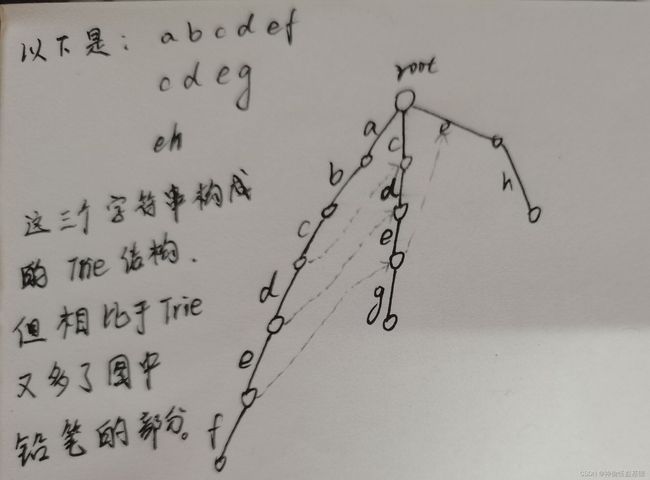
建立一个 AC 自动机有两个步骤:
- 基础的 Trie 结构:将所有的模式串构成一棵 Trie。
- KMP 的思想:对 Trie 树上所有的结点构造失配指针。
而铅笔部分就是失配指针fail,每个节点都有适配指针,没画的fail指针的节点都是指向root的,通过它就实现了KMP的效果(匹配到后面匹配不上了也能尽量利用前面匹配上的部分)
接下来我们看代码:
class ACAutomation {
static class Node {
// end 用于一个字符串的末尾节点存放当前字符串
// 路上经过的节点的 end 都是为 null 的
private String end;
private boolean endUse; // 用于记录是否已经收集过该字符串了
private Node fail; // 失配指针
private Node[] nexts = new Node[26];
}
Node root = new Node();
// 插入敏感词
// 在不调整fail指针的情况下先构造好Trie树
public void insert(String s) {
char[] str = s.toCharArray();
Node cur = root;
for (char c : str) {
int index = c - 'a';
if (cur.nexts[index] == null) {
cur.nexts[index] = new Node();
}
cur = cur.nexts[index];
}
cur.end = s;
}
// 设置好fail指针
// 如果对这里不是很理解,可以网上找个动态图看看就明白了,
// 光口头表达对于这个来说确实不好表达清楚,
// 虽然我理解这过程但我现在还不会画动图,感觉对不起大家呀,有空一定学学咋画
public void build() {
LinkedList list = new LinkedList<>(); // 用于层序遍历
list.add(root);
while (!list.isEmpty()) { // 经典的层序遍历
Node cur = list.poll();
// 在当前节点时去设置nexts中节点的fail指针
for (int i = 0; i < 26; i++) {
if (cur.nexts[i] != null) {
// 先让它指向root节点
cur.nexts[i].fail = root;
// 去看 cFail 节点的子节点能否成为 cur.nexts[i]失配指针指向的节点
Node cFail = cur.fail;
while (cFail != null) {
if (cFail.nexts[i] != null) {
cur.nexts[i].fail = cFail.nexts[i];
break;
}
cFail = cFail.fail;
}
list.add(cur.nexts[i]);
}
}
}
}
// 收集content中出现过的敏感词
public List containWords(String content) {
char[] str = content.toCharArray();
ArrayList res = new ArrayList<>();
Node cur = root;
for (char c : str) {
int index = c - 'a';
while (cur.nexts[index] == null && cur != root) {
cur = cur.fail;
}
cur = cur.nexts[index] != null ? cur.nexts[index] : root;
Node follow = cur;
while (follow != root) {
if (follow.endUse) { // 如果已经收集过了就不再收集了
break;
}
if (follow.end != null) {
res.add(follow.end);
follow.endUse = true;
}
follow = follow.fail;
}
}
return res;
}
}
好了今天的算法就到这了,希望能帮大家复习一下这块知识!