数据结构与算法——归并排序

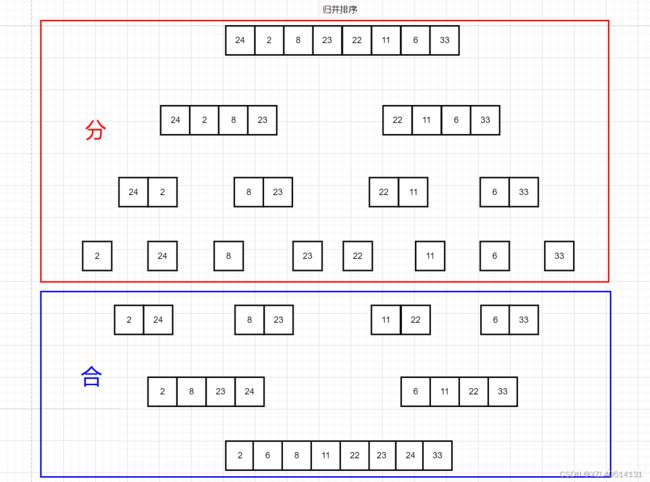
执行流程图

分而治之
将数组二分，一直分到不能再分为止
自底向上有序地合并数组

---

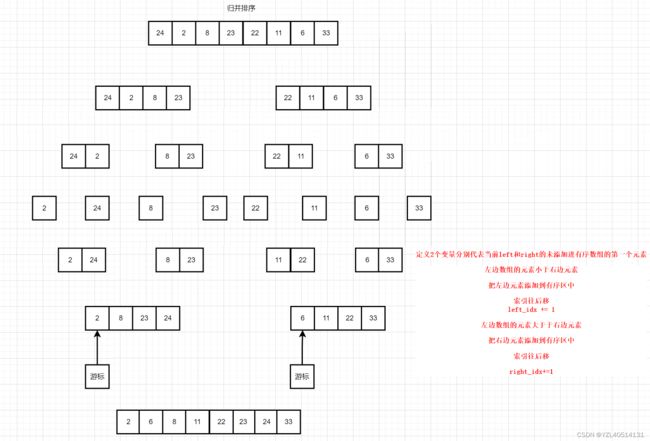
图文说明

代码实现

def merge(left, right):
    # 最终返回一个合并好的有序数组
    # 定义2个变量分别代表当前left和right的未添加进有序数组的第一个元素
    left_idx, right_idx = 0, 0
    res = []  # 有序数组
    while left_idx < len(left) and right_idx < len(right):
        # 左边数组的元素小于右边元素
        if left[left_idx] <= right[right_idx]:
            # 把左边元素添加到有序区中
            res.append(left[left_idx])
            # 索引往后移
            left_idx += 1
        else:
            # 把右边元素添加到有序区中
            res.append(right[right_idx])
            # 索引往后移
            right_idx += 1
    res += right[right_idx:]  # 把剩余未添加的元素全部添加到有序数组哦后面
    res += left[left_idx:]  # 为什么可以直接添加？因为left和right本身就是一个有序的数组
    # 如果left_idx走完了，right还剩一些元素，说明right里的剩下的元素全部有序数组的最后一个元素大
    return res


def mergeSort(nums):
    # 分
    # 数组不能再分了
    if len(nums) <= 1:
        return nums
    mid = len(nums) // 2  # 求出数组的中间位置
    print(nums[:mid], nums[mid:])
    left = mergeSort(nums[:mid])  # 左边的数组
    right = mergeSort(nums[mid:])  # 右边的数组
    # 合
    return merge(left, right)


test = [9, 3, 1, 2, 7, 5, 11, 22, 23, 24, 35, 55]
test = mergeSort(test)
print(test)

执行结果

[9, 3, 1, 2, 7, 5] [11, 22, 23, 24, 35, 55]
[9, 3, 1] [2, 7, 5]
[9] [3, 1]
[3] [1]
[2] [7, 5]
[7] [5]
[11, 22, 23] [24, 35, 55]
[11] [22, 23]
[22] [23]
[24] [35, 55]
[35] [55]
[1, 2, 3, 5, 7, 9, 11, 22, 23, 24, 35, 55]

Process finished with exit code 0

时间复杂度 O(nlogn)
稳定性：稳定

---