生成模型和判别模型学习

生成模型和判别模型

在机器学习中，一般将学习方式分为监督式学习和非监督式学习方式。

• 回忆一下，监督学习的任务就是从数据中学习一个模型，应用这一模型，对给定的输入X预测相应的输出Y。这个模型的一般形式为：决策函数Y=f(X)或者条件概率分布P(Y|X)。

监督学习又分为两类模型：判别模型 和 生成模型。

• 简单地说，判别式模型是针对条件分布建模，而生成式模型则针对联合分布进行建模。
  

先从一个例子直观理解：

---

任务：识别一个语音属于哪种语言。现在一个人和你说了一句话，你需要识别出他说的到底是汉语、英语还是法语等。

用生成模型的方法是学习每一种语言，你花了大量精力把汉语、英语和法语等都学会了，我指的学会是你知道什么样的语音对应什么样的语言。然后再有人过来对你说话，你就可以知道他的语言对应什么语言；
用判别模型的方法是不去学习每一种语言，你只学习这些语言模型之间的差别，然后再分类。意思是指我学会了汉语和英语等语言的发音是有差别的，我学会这种差别就好了。

---

所以生成模型实际上带的信息要比判别模型丰富，研究单类问题比判别模型灵活性强，模型可以通过增量学习得到，能用于数据不完整（missing data）情况。

基础概念

贝叶斯定理

贝叶斯定理是英国数学家贝叶斯提出来的。用来描述两个条件概率之间的关系。若记P（A）、P（B）分别表示事件A和事件B发生的概率，则：
P(A|B)：表示事件B发生的情况下，事件A发生的概率
P(AB) ：表示事件A和事件B同时发生的概率

有如下法则：

则可推导出：

或写为：

上式中：P(A)称为‘先验概率’，即在事件B发生之前 我们对事件A发生的概率做一个判断。
P(A|B) 称为‘后验概率’，即在事件B发生后，我们对事件A的概率重新做评估
P（B|A）/ P(B) 称为‘可能性函数’，这是一个调整因子，使得预估概率更接近真实概率。

监督学习

对于有监督学习，有两种定义。

1. 求决策函数Y=f(X)：（针对分类问题）
输入一个X（可以是原始数据如图像，声音，也可以是提取出来的特征向量），它就输出一个类别即标签值Y，这个Y与一个阈值比较，根据比较结果判定X属于哪个类别。例如两类（w1和w2）分类问题，如果Y大于阈值，X就属于类w1，如果小于阈值就属于类w2。这样就得到了该X对应的类别了。

2. 求条件概率分布P(Y|X)：
输入一个X，它通过比较它属于所有类的概率，然后输出概率最大的那个Y作为该X对应的类别。例如：如果P(w1|X)大于P(w2|X)，那么我们就认为X是属于w1类的。

生成模型和判别模型，都可以实现对给定的输入X 预测相应的输出Y的功能。

判别模型

由数据直接学习决策函数Y=f(X)或者条件概率分布P(Y|X)作为预测的模型，即判别模型。基本思想是有限样本条件下建立判别函数，不考虑样本的产生模型，直接研究预测模型。

判别方法关心的是对于给定的输入X，应该预测什么样的输出Y。
判别模型是寻找不同类别之间的最优分类面，反映的是异类数据之间的差异。

典型的判别模型：

1. 感知机
2. 决策树
3. 逻辑回归logic regression
4. K近邻 KNN
5. 最大熵模型
6. 支持向量机SVM
7. 提升方法Boosting
8. 神经网络NN
9. 高斯过程Gaussian process
10. 条件随机场CRF
11. CART(Classification and regression tree)

生成模型

估计的是联合概率分布（joint probability distribution），p(y, x)=p(y|x)*p(x)，由数据学习联合概率密度分布P(X,Y)，然后求出条件概率分布P(Y|X)作为预测的模型，即生成模型：P(Y|X)= P(X,Y)/ P(X)。基本思想是首先建立样本的联合概率概率密度模型P(X,Y)，然后再得到后验概率P(Y|X)，再利用它进行分类。

生成方法关心的是给定输入x产生输出y的生成关系。

已知输入变量x和目标变量y，先对它们的联合概率分布p(x, y)建模，然后计算样本属于每一个类的条件概率p(y|x)即类后验概率，按照这个值来完成分类，如将样本分到概率p(y|x)最大的那个类。根据概率论的知识，有：

求条件概率分布P(Y|X)，就得先求出P(X, Y)，和P(X)。

• P(X)就是你的训练数据的概率分布（需要训练数据样本非常多的时候，你得到的P(X)才能很好的描述你数据真正的分布）。
• 那P(X, Y)呢？

联合概率密度函数等于类概率p(y)与类条件概率p(x|y)即先验概率的乘积，即：

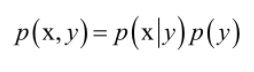
将上面两个公式合并起来，有：

这就是贝叶斯公式。它完成了因果转换，我们要完成的是由果推断因，而在训练时我们建立的是因到果的模型p(x|y)。如果我们假设特征向量x的每个分量相互独立，则可以得到朴素贝叶斯分类器，如果假设每个类的样本服从正态分布，则p(x|y)为正态分布，此时为正态贝叶斯分类器。
如果只用于分类而不需要给出具体的概率值，则分母p(x)对所有类型y都是一样的，只需要计算分子p(x|y)p(y)。

典型的生成模型：

1. 判别式分析
2. 朴素贝叶斯Native Bayes
3. 混合高斯型Gaussians
4. 隐马尔科夫模型HMM
5. 贝叶斯网络
6. sigmoid belief networks
7. 马尔科夫随机场Markov random fields
8. 深度信念网络DBN
9. 隐含狄利克雷分布简称LDA(Latent Dirichlet allocation)
10. 多专家模型（the mixture of experts model）
11. 变分自编码器
12. 生成对抗网络

优缺点对比

生成方法

优点：

1、可以还原联合分布率(判别式模型不可以)
2、学习的收敛速度更快，即：当样本容量增加的时候，学到的模型可以更快地收敛于真实模型
3、可以应付存在隐变量的情况，比如混合高斯模型就是含有隐变量的生成方法。

缺点：

1、浪费计算资源。联合分布是能提供更多的信息，但也需要更多的样本和更多计算，尤其是为了更准确估计类别条件分布，需要增加样本的数目，而且类别条件概率的许多信息是我们做分类用不到，因而如果我们只需要做分类任务，就浪费了计算资源。
2、实践中多数情况下判别模型效果更好

判别方法

优点：

• 节约了计算资源，相比较于生成模型而言
• 直接学习条件概率或者决策函数，学习效率更高
• 直接学习可以对数据进行各种程度上的的抽象、定义特征并使用特征，因此可以简化学习问题

缺点：

• 不能反映训练数据本身的特性。能力有限，可以告诉你的是1还是2，但没有办法把整个场景描述出来。
• Lack elegance of generative: Priors, 结构, 不确定性
  Alternative notions of penalty functions, regularization, 核函数
• 黑盒操作: 变量间的关系不清楚，不可视

两者的联系和区别

1、由生成模型可以得到判别模型，但由判别模型得不到生成模型。
2、当存在隐变量（当我们找不到引起某一现象的原因的时候，我们就把这个在起作用，但是，无法确定的因素，叫“隐变量”） 时，仍可以利用生成方法学习，此时判别方法不能用。