样本不均衡

这里主要介绍CV中的样本不均衡问题（部分方法也适用于ML中）。当前主流的物体检测算法，如Faster RCNN和SSD等，都是将物体检测当做分类问题来考虑，即先使用先验框或者RPN等生成感兴趣的区域，再对该区域进行分类与回归位置。这种基于分类思想的物体检测算法存在样本不均衡的问题，因而会降低模型的训练效率与检测精度。
下面首先分析样本不均衡带来的问题，随后会讲解两种经典的缓解不均衡问题的方法。

1、不均衡问题分析

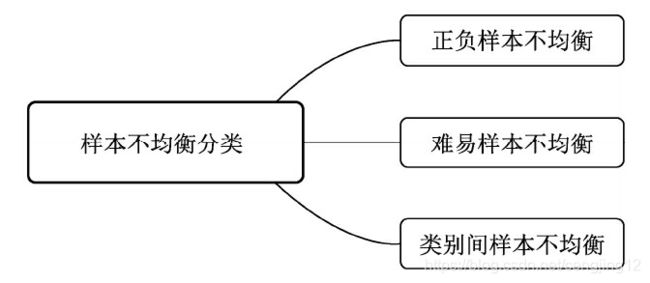
在当前的物体检测算法中，由于检测算法各不相同，以及数据集之间的差异，可能会存在正负样本、难易样本、类别间样本这3种不均衡问题，如图所示。下面将详细分析这3种不均衡问题的来源，以及常
用的解决方法。

1.1 正负样本不均衡

以Faster RCNN为例，在RPN部分会生成20000个左右的Anchor，由于一张图中通常有10个左右的物体，导致可能只有100个左右的Anchor会是正样本，正负样本比例约为1∶200，存在严重的不均衡。
对于物体检测算法，有核心价值的是对应着真实物体的正样本，在训练时会根据其loss来调整网络参数。相比之下，负样本对应着图像的背景，如果有大量的负样本参与训练，则会淹没正样本的损失，从而降低网络收敛的效率与检测精度。

1.2 难易样本不均衡

除了正负样本，在物体检测中还存在着难易样本的不均衡问题。根据是否容易学习及与标签的重叠程度，可以将所有样本分为4类：简单正样本（Easy Positive）、难正样本（Hard Positive）、简单负样本（Easy Negative）及难负样本（Hard Negative），如图所示。

难样本指的是分类不太明确的边框，处在前景与背景的过渡区域上，在网络训练中难样本损失会较大，也是我们希望模型去学习优化的样本，利用这部分训练可以提升检测的准确率。
然而，大量的样本并非处在前景与背景的过渡区，而是与真实物体没有重叠区域的负样本，或者与真实物体重叠程度很高的正样本，这部分被称为简单样本，单个损失会较小，对参数收敛的作用有限。虽然简单样本单个损失小，但由于数量众多，因此如果全都计算损失的话，其损失也会比难样本大很多，这种难易样本的不均衡也会影响模型的收敛与精度。

值得注意的是，由于负样本中大量的是简单样本，导致难易样本与正负样本这两个不均衡问题有一定的重叠，解决方法往往能同时对这两个问题起作用。

1.3 类别间样本不均衡

在有些物体检测的数据集中，还会存在类别间的不均衡问题。举个例子，数据集中有100万个车辆、1000个行人的实例标签，样本比例为1000∶1，属于典型的类别不均衡。

这种情况下，如果不做任何处理，使用该数据集进行训练，由于行人这一类别可参考标签太少，会使得模型主要关注车这一类别的检测，网络中的参数主要根据车辆的损失进行优化，导致行人的检测精度大大下降。

针对以上3种不均衡问题，经典的物体检测算法在处理样本时，总体上有如下4种缓解办法：

• Faster RCNN、SSD等算法在正负样本的筛选时，根据样本与真实物体的IoU大小，设置了3∶1的正负样本比例，这一点缓解了正负样本的不均衡，同时也对难易样本不均衡起到了作用。
• Faster RCNN在RPN模块中，通过前景得分排序筛选出了2000个左右的候选框，这也会将大量的负样本与简单样本过滤掉，缓解了前两个不均衡问题。
• 权重惩罚：对于难易样本与类别间的不均衡，可以增大难样本与少类别的损失权重，从而增大模型对这些样本的惩罚，缓解不均衡问题。
• 数据增强：从数据侧入手，可以在当前数据集上使用随机生成和添加扰动的方法，也可以利用网络爬虫数据等增加数据集的丰富性，从而缓解难易样本和类别间样本等不均衡问题，可以参考SSD的数据增强方法。

2、在线难样本挖掘：OHEM

针对难易样本不均衡的问题，2016年CVPR会议上的OHEM（Online Hard Example Mining）方法高效率地实现了在线难样本的挖掘，在多个数据集上都有着优越的表现，是一个很经典的难样本挖掘方法。

难样本挖掘的思想最初在机器学习中被广泛使用，一般被称为难负样本挖掘（Hard Negative Mining，HNM），用于解决类别的不均衡问题。以SVMs（Support Vector Machines，支持向量机）为例，HNM方法先让模型收敛于当前的工作数据集，然后固定该模型，在数据集中去除简单的样本，添加一些当前无法判断的样本，进行新的训练。这样的交替训练可以使得模型性能达到最优。

物体检测方法很难直接使用HNM算法进行挖掘。原因在于物体检测算法通常采用随机梯度下降（Stochastic Gradient Descent，SGD）等优化方法来进行优化，往往需要上万次的参数更新；而如果采用HNM交替训练的方法，每迭代几次就固定模型，训练的速度会大大下降。

OHEM可以看做是HNM在物体检测算法上的应用，在实现时选择了Fast RCNN作为基础检测算法。Fast RCNN与Faster RCNN类似，采用了两阶结构，在第二个阶段通过RCNN网络得到了边框的预测值，接下来使用了如下3点标准来确定正、负样本。

• 当前RoI与真实物体的IoU大于0.5时，判定为正样本。
• 当前RoI与真实物体的IoU大于0且小于0.5时，判定为负样本。
• 为了均衡正、负样本的数量，控制正、负样本的比例为1∶3，总数量不超过256。通过这种方式有效缓解了正、负样本的不均衡。

上述方法虽然简单有效，但是容易忽略一些较为重要的难负样本，并且固定了正、负样本的比例与最大数量，显然不是最优的选择。以此为出发点，OHEM将交替训练与SGD优化方法进行了结合，在每张图片的RoI中选择了较难的样本，实现了在线的难样本挖掘。

OHEM实现在线难样本挖掘的网络如图8.9所示。图中包含了两个相同的RCNN网络，上半部的a部分是只可读的网络，只进行前向运算；下半部的b网络即可读也可写，需要完成前向计算与反向传播。

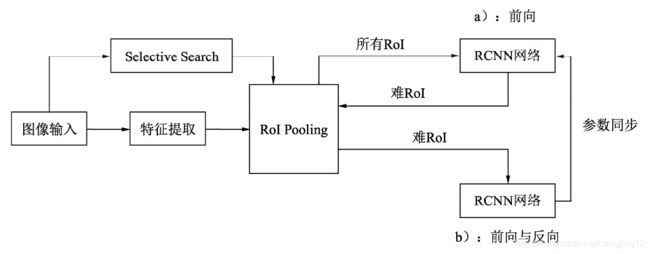
OHEM方法示意图
在一个batch的训练中，基于Fast RCNN的OHEM算法可以分为以下5步：
（1）按照原始Fast RCNN算法，经过卷积提取网络与RoI Pooling得到了每一张图像的RoI。
（2）上半部的a网络对所有的RoI进行前向计算，得到每一个RoI的损失。
（3）对RoI的损失进行排序，进行一步NMS操作，以去除掉重叠严重的RoI，并在筛选后的RoI中选择出固定数量损失较大的部分，作为难样本。
（4）将筛选出的难样本输入到可读写的b网络中，进行前向计算，得到损失。
（5）利用b网络得到的反向传播更新网络，并将更新后的参数与上半部的a网络同步，完成一次迭代。

当然，为了实现方便，OHEM也可以仅采用一个RCNN网络，在选择完难样本后将剩下的简单样本的损失置0，可以起到相同的作用。但是，由于其特殊的损失计算方式，把简单的样本都舍弃了，导致模型无法提升对于简单样本的检测精度，这也是OHEM方法的一个弊端。

总体上，OHEM是一个很经典的难样本挖掘Trick，实现方式简单，可以显著提升网络训练的效率和检测性能，被广泛地应用于难样本的挖掘场景中，并且数据集越大、难度越高，OHEM对于检测的提升越明显。

3、专注难样本：Focal Loss

当前一阶的物体检测算法，如SSD和YOLO等虽然实现了实时的速度，但精度始终无法与两阶的Faster RCNN相比。是什么阻碍了一阶算法的高精度呢？何凯明等人将其归咎于正、负样本的不均衡，并基于此提出了新的损失函数Focal Loss及网络结构RetinaNet，在与同期一阶网络速度相同的前提下，其检测精度比同期最优的二阶网络还要高。

从前面的叙述中可以得知，Faster RCNN在第一个阶段利用得分筛选出了2000个左右的RoI，可以过滤掉大部分的负样本，在第二个阶段通过固定正、负样本比例或者OHEM等方法，可以有效解决正、负样本的不均衡问题。

而对于SSD等一阶网络，由于其需要直接从所有的预选框中进行筛选，即使使用了固定正、负样本比例的方法，仍然效率低下，简单的负样本仍然占据主要地位，导致其精度不如两阶网络。

为了解决一阶网络中样本的不均衡问题，何凯明等人首先改善了分类过程中的交叉熵函数，提出了可以动态调整权重的Focal Loss。为了形成对比，接下来分别介绍标准交叉熵、平衡交叉熵及Focal Loss。

3.1 标准交叉熵损失

首先回顾一下标准的交叉熵（Cross Entropy，CE）函数，其形式如式所示。

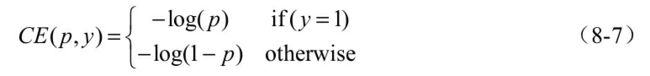
公式中，p代表样本在该类别的预测概率，y代表样本标签。可以看出，当标签为1时，p越接近1，则损失越小；标签为0时p越接近0，则损失越小，符合优化的方向。
为了方便表示，按照式（8-8）将p标记为pt：

则交叉熵可以表示为式（8-9）的形式：
$CE(p,y)=CE(p_t)=-log(pt)$　（8-9）
标准的交叉熵中所有样本的权重都是相同的，因此如果正、负样本不均衡，大量简单的负样本会占据主导地位，少量的难样本与正样本会起不到作用，导致精度变差。

3.2 平衡交叉熵损失

为了改善样本的不平衡问题，平衡交叉熵在标准的基础上增加了一个系数${\alpha }_t$来平衡正、负样本的权重，${\alpha }_t$由超参$\alpha$按照式（8-10）计算得来，$\alpha$取值在[0,1]区间内。

有了${\alpha }_t$，平衡交叉熵损失公式如式所示。
$CE(pt)=-{\alpha }_{t}log(p_t)$
尽管平衡交叉熵损失改善了正、负样本间的不平衡，但由于其缺乏对难易样本的区分，因此没有办法控制难易样本之间的不均衡。

3.3 专注难样本Focal Loss

Focal Loss为了同时调节正、负样本与难易样本，提出了如式所示的损失函数。

$$FL(p_t)=-{\alpha }_t(1-p_t{)}^{\gamma }log(p_t)$$

对于该损失函数，有如下3个属性：

• 与平衡交叉熵类似，引入了${\alpha }_t$权重，为了改善正负样本的不均衡，可以提升一些精度。
• $(1-p_t{)}^{\gamma }$是为了调节难易样本的权重。当一个边框被误分类时，$p_t$较小，则$(1-p_t{)}^{\gamma }$接近于1，其损失几乎不受影响；当$p_t$接近于1时，表明其分类预测较好，是简单样本，$(1-p_t{)}^{\gamma }$接近于0，因此其损失被调低了。
• $\gamma$是一个调制因子，$\gamma$越大，简单样本损失的贡献会越低。

为了验证Focal Loss的效果，何凯明等人还提出了一个一阶物体检测结构RetinaNet，其结构如图所示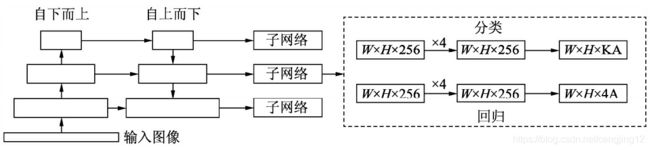

对于RetinaNet的网络结构，有以下5个细节：

• 在Backbone部分，RetinaNet利用ResNet与FPN构建了一个多尺度特征的特征金字塔。
• RetinaNet使用了类似于Anchor的预选框，在每一个金字塔层，使用了9个大小不同的预选框。
• 分类子网络：分类子网络为每一个预选框预测其类别，因此其输出特征大小为KA×W×H，A默认为9，K代表类别数。中间使用全卷积网络与ReLU激活函数，最后利用Sigmoid函数输出预测值。
• 回归子网络：回归子网络与分类子网络平行，预测每一个预选框的偏移量，最终输出特征大小为4A×W×W。与当前主流工作不同的是，两个子网络没有权重的共享。
• Focal Loss：与OHEM等方法不同，Focal Loss在训练时作用到所有的预选框上。对于两个超参数，通常来讲，当γ增大时，α应当适当减小。实验中γ取2、α取0.25时效果最好。

总体上，Focal Loss算法将样本的不均衡视为一阶与两阶网络精度差距的原因，提出了简单高效的Focal Loss，使得模型专注于难样本上，并提出了一阶网络RetinaNet，实现了SOTA的精度。