拓扑排序（Topological Sort）

问题引入

现实生活中我们遇到的要处理的事情可能要讲究先后顺序，比如说要先穿好衬衫才能穿外套，再比如说一个计算机系的学生想修完所有课程：

面对这样一张图，如何求出做事的顺序？这时需要拓扑排序：
将事件视为点，先后关系视为边，则可以把“先做事件2，再做事件1”抽象成：2→1，同理可将上面的课表变成一副有向图：

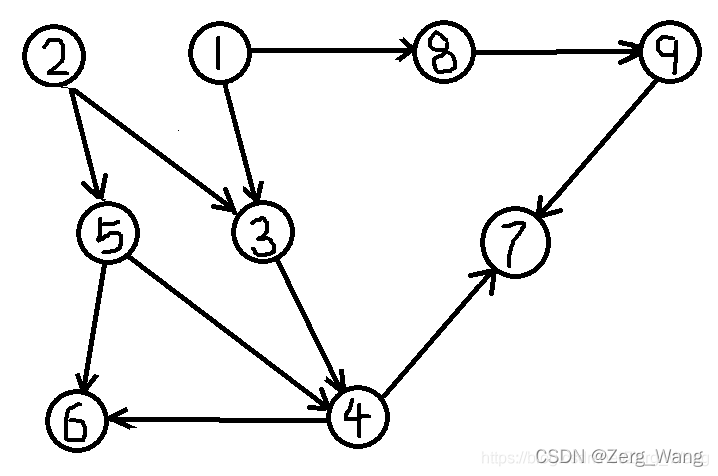
一个可以进行拓扑排序的有向图是不能存在环的：

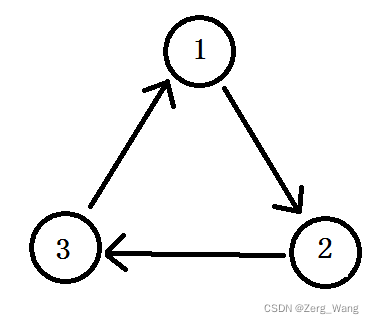
如上图表示了一个环，在实际问题中，就表示完成事件2前要完成事件1，完成事件3前要完成事件2，但完成事件1前要完成事件3，这样无限循环，3件事都做不了。

拓扑排序算法

拓扑排序就是通过以上这种有向图来获知做这一系列事情的先后顺序。算法的主要步骤有：

1. 在图中找到一个入度为0的点（入度为零表示没有别的点指向该点，找不到入度为0的点说明有向图中存在环）

2. 输出该点并将该点的所有边删除（删除边的操作，即为将该点指向的所有点的入度减1）

3. 重复步骤1、2，直到所有点输出（如果所有点还没输出完，就找不到入度为0的点，说明有向图中存在环）

为了防止每次找入度为0的点时都要遍历图中所有点，可以在一开始就将所有入度为0的点记录下来，记为 $Q=\{N_1,N_2...N_k\}$，每次从 $Q$ 中找点 $N_i(1\le i\le k)$ 删边后，只会改变 $N_i$ 指向的点的入度，因此每次删边后将 $N_i$ 指向的点中入度为0的加入到 $Q$ 即可。在代码上，$Q$ 可以使用队列来实现：

#include 
#include 
using namespace std;

#define MAXN 100
int point[MAXN][MAXN], indeg[MAXN], ans[MAXN];
bool a[MAXN][MAXN];             //a[i][j]为真，说明 i --> j
int n, m, total;                
queue <int> q;

//点i指向的点的数量（也就是出度）为point[i][0]，point[i][1]到point[i][point[i][0]]存储这point[i][0]个点
 
int main(){
    cin>>n>>m;  //表示有n件事，m个先后关系（m条边）
    for (int i=1; i<=m; i++){
        int a1, a2;
        cin>>a1>>a2;    //输入a1 a2表示a1 --> a2  
        if (a[a2][a1]){          
            cout<<"No answer"<<endl; //若a1 --> a2的同时还有a1 --> a2说明有环
            return 0;
        }
        if (!a[a1][a2]){   //防止重复输入
            point[a1][++point[a1][0]] = a2;
            a[a1][a2] = 1;
            indeg[a2]++;  //indeg数组统计每个点的入度，从而判断重边与环
        }
    }
    
    for (int i=1; i<=n; i++)
        if (!indeg[i]) q.push(i);   //将所有入度为零的点放入q中
    
    if (q.empty()) {
        cout<<"No answer"<<endl;    //若无入度为0的点说明有环
        return 0;
    }

    for (;;){
        total++;
        int cp = q.front(); //cp，即当前操作的点（current point）
        ans[total] = cp;
        for (int i=1; i<=point[cp][0]; i++) 
            if (!(--indeg[point[cp][i]])) 
                q.push(point[cp][i]);   //删边并找点
    
        q.pop();

        if (q.empty()){
            if (total!=n)           //判断是否输出了n个点
                cout<<"No answer";
            else
                for (int i=1;i<=total;i++) cout<<ans[i]<<" ";//如果是说明排序完毕，否则说明有环
            return 0;
        }
    }
    return 0;
} 

LeetCode 207

链接：207. Course Schedule

bool canFinish(int numCourses, int** prerequisites, int prerequisitesSize, int* prerequisitesColSize){
    
    int queueTail = -1, queueHead = 0, numUsed = 0;
    int que[numCourses];
    int indegree[numCourses];
    memset(indegree, 0, sizeof(indegree));
    bool ifPreRequire[numCourses][numCourses];
    memset(ifPreRequire, 0, sizeof(ifPreRequire));

    for (int i=0; i<prerequisitesSize; i++) {
        int preCourse = prerequisites[i][1];
        int curCourse = prerequisites[i][0];
        indegree[curCourse]++;
        ifPreRequire[preCourse][curCourse] = 1;
    }

    for (int i=0; i<numCourses; i++) 
        if (!indegree[i]) {
            queueTail++;
            que[queueTail] = i;
        }

    while (queueHead <= queueTail) {
        int curCourse = que[queueHead];
        numUsed++;
        queueHead++;
        for (int i=0; i<numCourses; i++) 
            if (ifPreRequire[curCourse][i] && i!=curCourse) {
                indegree[i]--;
                if (!indegree[i]) {
                    queueTail++;
                    que[queueTail] = i;
                }
            }
    }

    if (numUsed == numCourses) return 1;
    else return 0;
}

LeetCode 2392

链接：https://leetcode.com/problems/build-a-matrix-with-conditions/

将1到k的k个数字放在一个k*k的方格中（不放这k个数字的地方用0填充）。在放置时，还要满足某些数字要在另一些数字的左边或上边。给出这些限制条件，生成一个满足上述条件的方格。

int GetSort(int **a, int n, int k, int *queue) {
    bool f[k+1][k+1];
    memset(f, 0, sizeof(f));
    
    int inDegree[k+1];
    int head = 0, tail = 0, qSize = 0;
    memset(queue, 0, k*sizeof(int));
    memset(inDegree, 0, sizeof(inDegree));
    
    for (int i=0; i<n; i++) {
        if (f[a[i][0]][a[i][1]])  //同一个限制条件出现多次，会影响元素的入度
            continue;
        f[a[i][0]][a[i][1]] = 1;
        inDegree[a[i][1]]++;
    }        
    
    for (int i=1; i<=k; i++) 
        if (!inDegree[i])
            queue[qSize++] = i;
    
    if (!qSize)
        return 1;   //检测环
    else 
        tail = qSize-1;
    
    while (head<=tail) {
        int now = queue[head];
        for (int i=1; i<=k; i++)
            if (f[now][i]) {
                inDegree[i]--;
                if (!inDegree[i]) {
                    queue[++tail] = i;
                    qSize++;
                }                    
            }
        head++;
    }
    
    if (qSize!=k)   //检测环
        return 1;
    
    return 0;
}


int** buildMatrix(int k, int** r, int rSize, int* rowConditionsColSize, int** c, int cSize, int* colConditionsColSize, int* returnSize, int** returnColumnSizes){
    
    int rSort[k], cSort[k]; 
    if (GetSort(r, rSize, k, rSort)) {
        *returnSize = 0;
        return NULL;    //按行号由小到大放置元素，rSort[i]表示元素rSort[i]应放置在第i行
    }        
    if (GetSort(c, cSize, k, cSort)){
        *returnSize = 0;
        return NULL;   //按列号由小到大放置元素，cSort[i]表示元素cSort[i]应放置在第i列
    }    
    
    int ** ans = (int**)malloc(k*sizeof(int*));
    *returnSize = k;
    *returnColumnSizes = (int*)malloc(k*sizeof(int));
    for (int i=0; i<k; i++) {
        int* newAns = (int*)calloc(k, sizeof(int));
        ans[i] = newAns;
        (*returnColumnSizes)[i] = k;
    }
    
    int pos[k+1][2];    
    for (int i=0; i<k; i++) {
        pos[rSort[i]][0] = i;
        pos[cSort[i]][1] = i;
    }
    
    for (int i=1; i<=k; i++)
        ans[pos[i][0]][pos[i][1]]= i;
    
    return ans;
}